"时间倾诉我的故事"
- 1. 理论推导
- 2. 主流解法
- 3. 用EKF估计状态
- 3.1. 基于EKF代表解法的感悟
- 4. 用BA法估计状态
- 4.1 构建最小二乘问题
- 4.2 求解BA推导
- 4.3 H的稀疏结构
- 4.4 根据H稀疏性求解
- 4.5 鲁棒核函数
- 4.6 编程注意
- 5.总结
引入:
- 前端里程计能给出一个短时间内的轨迹和地图,时间长则不准确;
- 为了得到长时间内最优轨迹和地图,构建一个规模更大的优化问题。在后端优化中,通常考虑更长时间内的状态估计问题。
1. 理论推导
还是摆出最经典的SLAM运动和观测方程
f
(
x
)
=
{
x
k
=
f
(
x
k
−
1
,
u
k
)
+
w
k
z
k
,
j
=
h
(
y
j
,
x
k
)
+
v
k
,
j
f(x)= \begin{cases} x_k = f(x_{k-1}, u_k) + w_k \\ z_{k,j} = h(y_j, x_k) + v_{k,j} \end{cases}
f(x)={xk=f(xk−1,uk)+wkzk,j=h(yj,xk)+vk,j
实际上要解决: 拥有某些运动数据
u
u
u 和观测数据
z
z
z 时,如何确定状态量
x
x
x 和
y
y
y 的分布。
- 解决如下:
令 x k x_k xk 为 k k k 时刻所有的未知量, x k ≜ { x k , y 1 , . . . , y m } x_k \triangleq \{x_k, y_1,...,y_m \} xk≜{xk,y1,...,ym}
同时,令 k 时刻所有的观测值为 z k z_k zk。
代入上式,运动和观测方程以后如下:
f ( x ) = { x k = f ( x k − 1 , u k ) + w k z k , j = h ( y j , x k ) + v k , j f(x)= \begin{cases} x_k = f(x_{k-1}, u_k) + w_k \\ z_{k,j} = h(y_j, x_k) + v_{k,j} \end{cases} f(x)={xk=f(xk−1,uk)+wkzk,j=h(yj,xk)+vk,j
在 k k k 时刻,用 0 − k 0-k 0−k 的数据估计现在的状态分布:
P ( x k ∣ x 0 , u 1 : k , z 1 : k ) ⇓ B a y e s 法则交换 z 和 x P ( z k ∣ x k ) P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) ⇓ 按 x k − 1 时刻为条件概率展开 ∫ P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) d x k − 1 P(x_k|x_0, u_{1:k}, z_{1:k}) \\\;\\\Downarrow Bayes法则交换z和x \\\;\\ P(z_k|x_k)P(x_k|x_0, u_{1:k},z_{1:k-1}) \\\;\\\Downarrow 按x_{k-1}时刻为条件概率展开 \\\;\\ \int P(x_k|x_{k-1}, x_0, u_{1:k}, z_{1:k-1})P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1})\, \text d x_{k-1} P(xk∣x0,u1:k,z1:k)⇓Bayes法则交换z和xP(zk∣xk)P(xk∣x0,u1:k,z1:k−1)⇓按xk−1时刻为条件概率展开∫P(xk∣xk−1,x0,u1:k,z1:k−1)P(xk−1∣x0,u1:k,z1:k−1)dxk−1
2. 主流解法
上式 ∫ P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) d x k − 1 \int P(x_k|x_{k-1}, x_0, u_{1:k}, z_{1:k-1})P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1})\, \text d x_{k-1} ∫P(xk∣xk−1,x0,u1:k,z1:k−1)P(xk−1∣x0,u1:k,z1:k−1)dxk−1
主流的有两种做法:
-
- 假设马尔科夫性,当前状态仅和上个时态有关,用EKF等滤波器方法做状态估计;前两讲讲到过
-
- 当前状态和之前所有状态都有关系,基于BA用非线性优化等优化框架做。
3. 用EKF估计状态
在马尔科夫性成立后,当前状态仅和上个时态有关,上边左右式可分别简化为(右式中,
u
k
u_k
uk 和
k
−
1
k-1
k−1 时刻的状态无关,拿掉!):
左边:
P
(
x
k
∣
x
k
−
1
,
x
0
,
u
1
:
k
,
z
1
:
k
−
1
)
=
P
(
x
k
∣
x
k
−
1
,
u
k
)
右边:
P
(
x
k
−
1
∣
x
0
,
u
1
:
k
,
z
1
:
k
−
1
)
=
P
(
x
k
−
1
∣
x
0
,
u
1
:
k
,
z
1
:
k
−
1
)
左边:\qquad P(x_k|x_{k-1}, x_0, u_{1:k}, z_{1:k-1}) = P(x_k|x_{k-1}, u_k)\\\; \qquad右边:\qquad P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1}) = P(x_{k-1}|x_0, u_{1:k}, z_{1:k-1})
左边:P(xk∣xk−1,x0,u1:k,z1:k−1)=P(xk∣xk−1,uk)右边:P(xk−1∣x0,u1:k,z1:k−1)=P(xk−1∣x0,u1:k,z1:k−1)
- 由前边的两节知识,可知上式中我们只需维护一个状态量即可,不断迭代更新即可。假设它满足高斯分布,只需要考虑维护状态量的均值和协方差即可。
- 另记: x ^ \hat x x^ 表示先验, x ˉ \bar x xˉ 表示后验
根据高斯分布性质可得EKF中的预测环节:
P
(
x
k
∣
x
0
,
u
1
:
k
,
z
1
:
k
−
1
)
=
N
(
A
k
x
ˉ
k
−
1
+
u
k
,
A
k
P
^
k
−
1
A
k
T
+
R
)
=
记为
N
(
x
ˉ
k
,
P
ˉ
k
)
P(x_k|x_0,u_{1:k}, z_{1:k-1}) = N(A_k\bar x_{k-1}+u_k, \;\;\;A_k\hat P_{k-1}A_k^T+R) = 记为\quad N(\bar x_k, \bar P_k)
P(xk∣x0,u1:k,z1:k−1)=N(Akxˉk−1+uk,AkP^k−1AkT+R)=记为N(xˉk,Pˉk)
如此,就可以带入我们的EKF中进行使用。
3.1. 基于EKF代表解法的感悟
运算快,资源低;
局限:
-
- 马尔科夫性质—无法解决类似回环等当前状态与很久之前数据有关的问题
-
- 对 x k x_k xk 在当前时刻的一次线性化,计算出后验概率,是假设该点的线性化在后验概率处还是有效的,实际上不然。只有小范围成立,在远处的地方并不能近似,这是EKF的 非线性误差 。
- 2.1 而在非线性优化方法中,在每迭代一次,状态发生改变后就会做一阶或者二阶近似,重新做泰勒展开,适用范围更加广泛,状态变化大时候也适用。
-
- EKF SLAM不可适用于大场景,landmark多的时候,均值和方差是很大的。
4. 用BA法估计状态
BA(Bundle Adjustment):源于三维重建,在这里的意义是 通过不断调整相机的姿态和特征点的位置,使从每一个特征点反射出来的几束光线都收束到相机中心,类似求解只有观测方程的SLAM问题。
4.1 构建最小二乘问题
针对此问题,观测方程:
z = h ( ξ , p ) z = h(\xi, p) z=h(ξ,p)
ξ
\xi
ξ 是位姿(李代数表示) ,
p
p
p 是路标(特征点的位置), 观测误差如下:
e
=
z
−
h
(
ξ
,
p
)
e = z - h(\xi, p)
e=z−h(ξ,p)
代价函数(Cost Function)如下:
1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ e i j ∣ ∣ 2 = 1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ z i j − h ( ξ i , p j ) ∣ ∣ 2 \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||e_{ij}||^2 = \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||z_{ij}-h(\xi_{i},p_j)||^2 21i=1∑mj=1∑n∣∣eij∣∣2=21i=1∑mj=1∑n∣∣zij−h(ξi,pj)∣∣2
- 其中 z ( i , j ) z(i,j) z(i,j) 表示在位姿 ξ i \xi_i ξi 处观察路标 p j p_j pj 产生的数据。当该式最小时,我们的估计位姿 ξ i \xi_i ξi 和 路标 p j p_j pj 最接近真实值。
为了便于理解这里的 h h h ,举在相机中的例子:
- 这里
h
h
h 表示将世界坐标下的点
p
[
x
,
y
,
z
]
p[x,y,z]
p[x,y,z] 转到像素坐标(也就是程序可读图片的点位置的坐标)下的点
u
,
v
u,v
u,v :如下

这就是一个观测方程 h h h 的一种具体参数化的过程。
4.2 求解BA推导
再看要求解的非线性最小二乘问题( h h h 非线性显然 ):
1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ z i j − h ( ξ i , p j ) ∣ ∣ 2 \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||z_{ij}-h(\xi_{i},p_j)||^2 21i=1∑mj=1∑n∣∣zij−h(ξi,pj)∣∣2
首先定义要优化的变量:
x = [ ξ 1 , . . . , ξ m , p 1 , . . . , p n ] T x = [\xi_1, ..., \xi_m,p_1, ..., p_n]^T x=[ξ1,...,ξm,p1,...,pn]T
注意:虽然一个误差项针对的是单个位姿和路标点,但是在整体BA中,必须将优化变量定义为所有待优化的变量。
根据前文:求解非线性问题,要给一个小增量和增量方向,最终要求的也是这个 Δ x \Delta x Δx,这里给增量以后的代价函数为:
1 2 ∣ ∣ f ( x + Δ x ) ∣ ∣ 2 ≈ 1 2 ∑ i = 1 m ∑ j = 1 n ∣ ∣ e i j + F i j Δ ξ i + E i j Δ p j ∣ ∣ 2 \frac{1}{2}||f(x+\Delta x)||^2 \approx \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^n||e_{ij}+F_{ij}\Delta \xi_i + E_{ij}\Delta p_j||^2 21∣∣f(x+Δx)∣∣2≈21i=1∑mj=1∑n∣∣eij+FijΔξi+EijΔpj∣∣2
其中 F i j F_{ij} Fij 表示代价函数对相机姿态的偏导数, E i j E_{ij} Eij 表示对路标点位置的偏导数。
将相机位姿,和空间点变量分别放在一起:上式如下:
x c = [ ξ 1 , ξ 2 , . . . , ξ m ] T ∈ R 6 m , x p = [ p 1 , p 2 , . . . , p m ] T ∈ R 3 n ⇓ 1 2 ∣ ∣ f ( x + Δ x ) ∣ ∣ 2 = 1 2 ∣ ∣ e + F Δ x c + E Δ x p ∣ ∣ 2 x_c = [\xi_1, \xi_2, ..., \xi_m]^T \in \R^{6m}, \qquad x_p = [p_1, p_2, ..., p_m]^T \in \R^{3n} \\\;\Downarrow\\\;\\ \frac{1}{2}||f(x+\Delta x)||^2 = \frac{1}{2} ||e + F\Delta x_c + E \Delta x_p||^2 xc=[ξ1,ξ2,...,ξm]T∈R6m,xp=[p1,p2,...,pm]T∈R3n⇓21∣∣f(x+Δx)∣∣2=21∣∣e+FΔxc+EΔxp∣∣2
根据前边的非线性优化,最终我们要面临
H Δ x = g H \Delta x = g HΔx=g
而求解它要用的雅克比矩阵可以根据位姿和路标分别定义为:
J = [ F E ] J = [F \quad E] J=[FE]
则:
H
=
J
T
J
=
[
F
T
F
F
T
E
E
T
F
E
T
E
]
H = J^TJ= \begin{bmatrix} F^TF & F^TE \\ E^TF & E^TE \end{bmatrix}
H=JTJ=[FTFETFFTEETE]
点越多,就代表这个H的维度越大,计算复杂,资源占得多,接下来分析如何观察这个 H H H 的特点。
4.3 H的稀疏结构
根据前边,我们知道 H = J T J H = J^TJ H=JTJ, H H H的研究放在 J J J 上,对于J,考虑一个 e i j e_{ij} eij 它的表述如下:
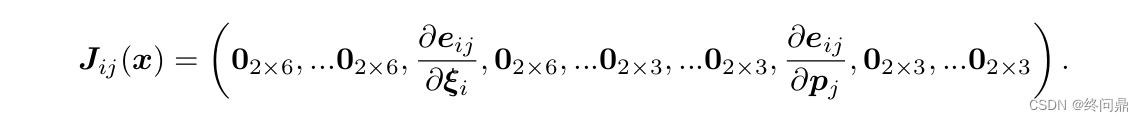
几何意义就是:它只涉及第 i 个矩阵和第 j 个路标,其余都为0,描述的是
ξ
i
\xi_i
ξi看到
p
j
p_j
pj 这件事,且前边的是位姿导数(6维),后边的是路标(三维)。
- 举例说明
假设有2个相机,6个路标。可视化它们的关系如下(可以观测到,则底下用实线连接):
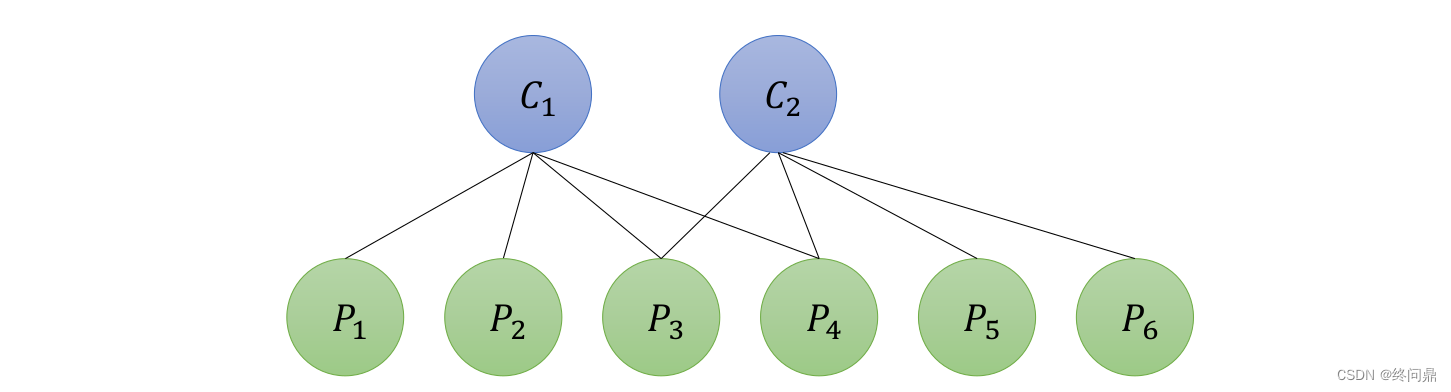 根据上边,把
C
1
C_1
C1 观察到
P
1
P_1
P1 的雅克比直观出来,则如下,因为
C
1
C_1
C1 六维:
根据上边,把
C
1
C_1
C1 观察到
P
1
P_1
P1 的雅克比直观出来,则如下,因为
C
1
C_1
C1 六维:
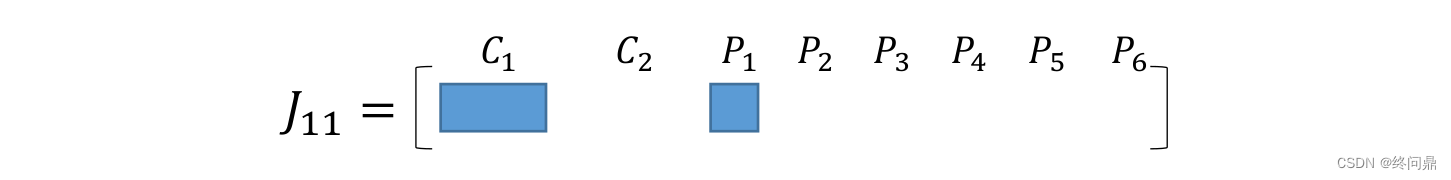
这个时候,将所有
J
i
j
J_{ij}
Jij 和 它们相乘之后的
H
H
H 同样直观展示:
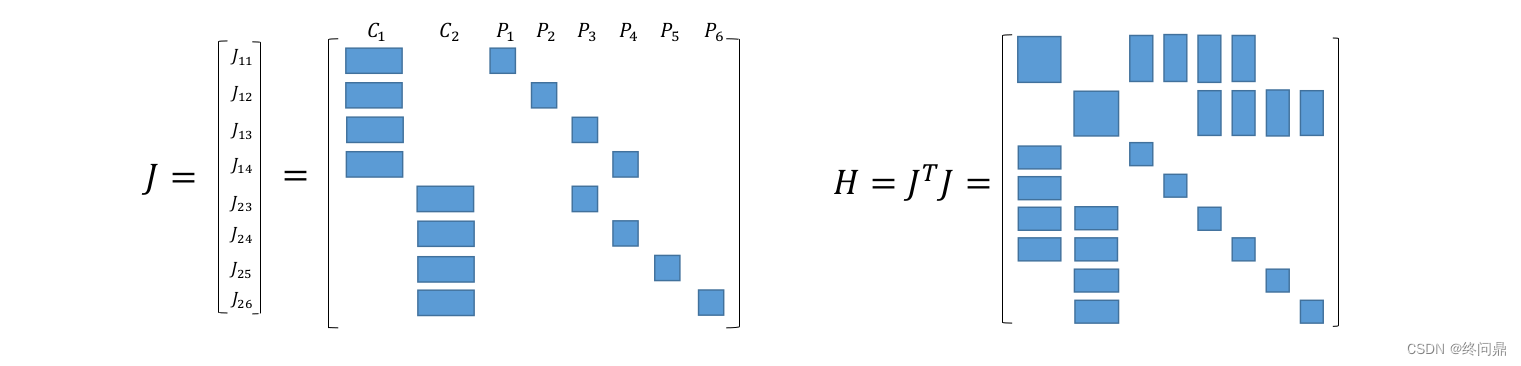
我们发现:H对应邻接矩阵,可以知道 假如
C
i
C_i
Ci 可以观察到
P
j
P_j
Pj ,那么
H
i
j
H_{ij}
Hij 则是有值的,否则是为0.如下:
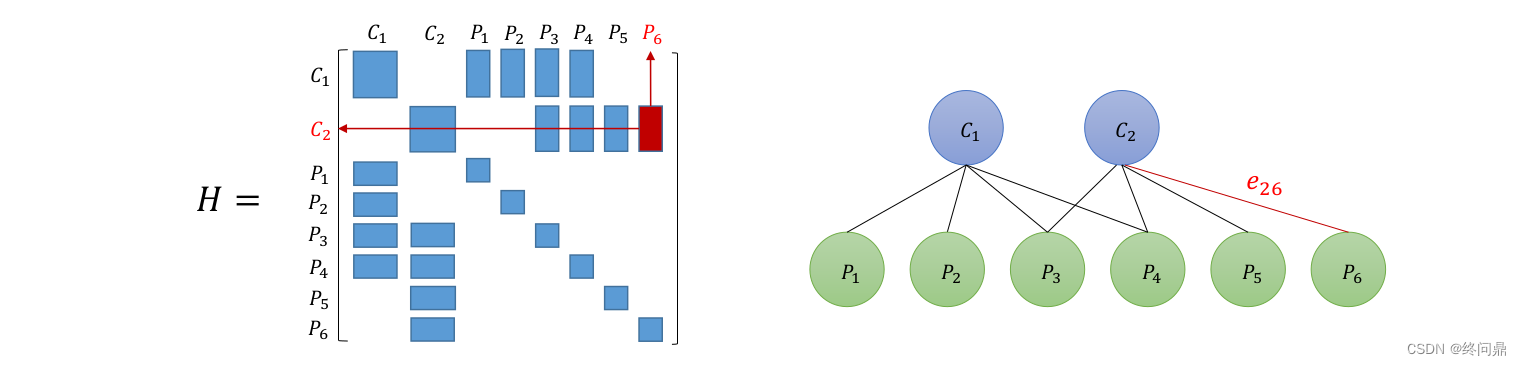
4.4 根据H稀疏性求解
根据以上H性质,可以将H分块为:其中
B
B
B 纯位姿,
C
C
C对角线纯路标,B非对角非零表示共视关系:
H
=
[
B
E
E
T
C
]
H = \begin{bmatrix} B & E \\ E^T & C \end{bmatrix}
H=[BETEC]
这个时候就可以求解 H Δ x = g H \Delta x = g HΔx=g 这个方程:
[ B E E T C ] [ Δ x c Δ x p ] = [ v w ] \begin{bmatrix} B & E \\ E^T & C \end{bmatrix} \begin{bmatrix}\Delta x_c \\ \Delta x_p\end{bmatrix} = \begin{bmatrix} v \\w \end{bmatrix} [BETEC][ΔxcΔxp]=[vw]
此时通过Schur消元(也叫边缘化)—就是先求一个比如 Δ x c \Delta x_c Δxc 然后再反代回去求 Δ x p \Delta x_p Δxp 的方法去求解。
4.5 鲁棒核函数
- 说明问题:我们采用的是误差项的二范数平方和,如果出现误匹配,单个项的误差就很大,此时优化算法会均摊误差去调整其他正确的数据。
- 问题原因:误差很大时,二范数增长过快(平方嘛)
- 解决:鲁棒核函数–把二范数度量换成增长较低,同时保证光滑(求导要求)的表述,因为它使得整个优化结果更为鲁棒,所以又叫它鲁棒核函数(Robust Kernel)。
列举一个常见的鲁棒核函数,Huber核:
f
(
x
)
=
{
1
2
e
2
i
f
∣
e
∣
≤
δ
,
δ
(
∣
e
∣
−
1
2
δ
)
o
t
h
e
r
w
i
s
e
.
f(x)= \begin{cases} \frac{1}{2}e^2 \qquad\qquad\qquad if|e| \le \delta, \\ \delta(|e| - \frac{1}{2} \delta)\qquad\quad otherwise . \end{cases}
f(x)={21e2if∣e∣≤δ,δ(∣e∣−21δ)otherwise.
它的图像如下:
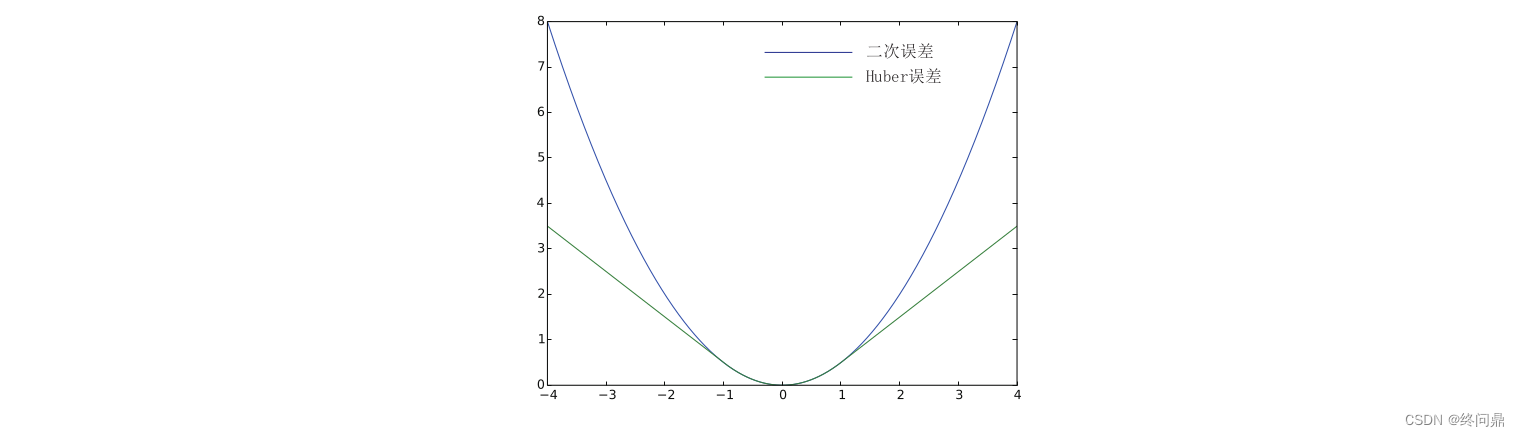
此外还有Cauchy核,Tukey核等。
4.6 编程注意
在使用G2O求解时,所有点云都要进行Schur,因为定义的Matrix维度仅仅是相机姿态参数的维度,要确保它不包含其他路标维度,不然报错。
5.总结
- 假设马尔科夫,EKF代表的滤波器模型
- 考虑所有状态,构成最小二乘问题,只有观测时又称BA。