目录

立方体由三角形构成

视点和视线

视点、观察目标点和上方向

视点：

观察目标点：

上方向：

在WebGL中，观察者的默认状态应该是这样的：

视图矩阵程序（LookAtTriangles.js） 

 实际上，“根据自定义的观察者状态，绘制观察者看到的景象”与“使用默认的观察状态，但是对三维对象进行平移、旋转等变换，再绘制观察者看到的景象”，这两种行为是等价的。（归根结底：不论视图怎样变化，无疑就是旋转、平移等操作，最终本质上都是对物体进行相反方向的旋转平移（默认的视角））

移动视点和移动被观察对象等效

从指定视点观察旋转后的三角形

＜旋转后顶点坐标＞=＜旋转矩阵＞×＜原始顶点坐标＞

＜“从视点看上去”的旋转后顶点坐标＞=＜视图矩阵＞×＜旋转后顶点坐标＞

＜“从视点看上去”的旋转后顶点坐标＞=＜视图矩阵＞×＜旋转矩阵＞×＜原始顶点坐标＞

＜视图矩阵＞×＜模型矩阵＞×＜原始顶点坐标＞

模型视图矩阵程序（LookAtRotatedTriangles.js） 

模型视图矩阵

＜模型视图矩阵＞=＜视图矩阵＞×＜模型矩阵＞

＜模型视图矩阵＞×＜顶点坐标＞

---

立方体由三角形构成

三维物体也是由二维图形（特别是三角形）组成的。如下图所示，12个三角形组成了一个立方体。

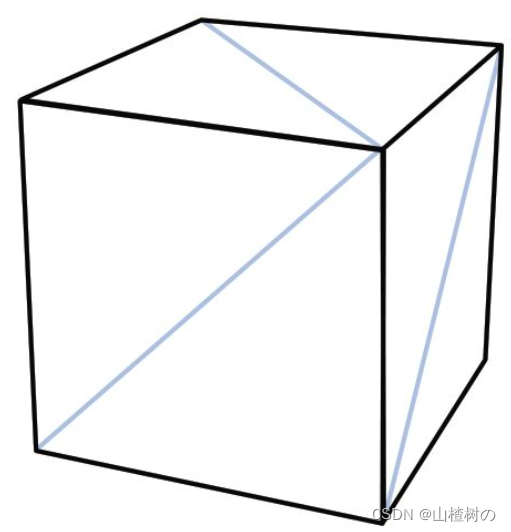
既然三维物体是由三角形组成的，那么则需要逐个绘制组成物体的每个三角形，最终就可以绘制出整个三维物体了。但是，三维与二维还有一个显著区别：在绘制二维图形时，只需要考虑顶点的x和y坐标，而绘制三维物体时，还得考虑它们的深度信息（depth information）。那就开始吧，首先我们来研究一下如何定义三维世界的观察者：在什么地方、朝哪里看、视野有多宽、能看多远。

视点和视线

三维物体与二维图形的最显著区别就是，三维物体具有深度，也就是Z轴。因此，你会遇到一些之前不曾考虑过的问题。事实上，我们最后还是得把三维场景绘制到二维的屏幕上，即绘制观察者看到的世界，而观察者可以处在任意位置观察。为了定义一个观察者，你需要考虑以下两点：

● 观察方向，即观察者自己在什么位置，在看场景的哪一部分？

● 可视距离，即观察者能够看多远？

我们将观察者所处的位置称为视点（eye point），从视点出发沿着观察方向的射线称作视线（viewing direction）。本次将研究如何通过视点和视线来描述观察者。到下面我们再来研究“观察者能看多远”的问题。 

我们来创建一个新的示例程序LookAtTriangles。在程序中，视点位于（0.20，0.25，0.25），视线向着原点（0，0，0）方向，可以看到原点附近有三个三角形。程序中的这三个三角形前后错落摆放，以帮助你理解三维场景中深度的概念。下图显示了LookAtTriangles的运行结果。

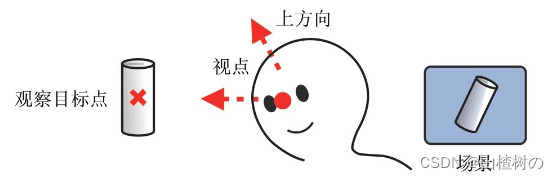
视点、观察目标点和上方向

为了确定观察者的状态，你需要获取两项信息：视点，即观察者的位置；观察目标点（look-at point），即被观察目标所在的点，它可以用来确定视线。此外，因为我们最后要把观察到的景象绘制到屏幕上，还需要知道上方向（up direction）。有了这三项信息，就可以确定观察者的状态了。下面将逐一进行解释（见下图）。

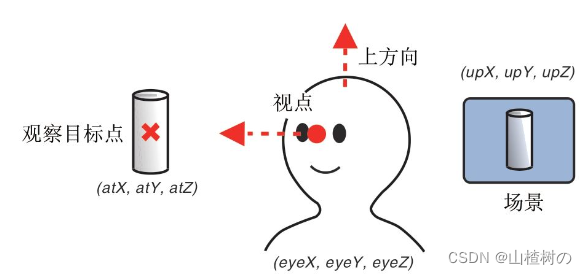
视点：

观察者所在的三维空间中位置，视线的起点。在接下来的几节中，视点坐标都用（eyeX，eyeY，eyeZ）表示。 

观察目标点：

被观察目标所在的点。视线从视点出发，穿过观察目标点并继续延伸。注意，观察目标点是一个点，而不是视线方向，只有同时知道观察目标点和视点，才能算出视线方向。观察目标点的坐标用（atX，atY，atZ）表示。

上方向：

最终绘制在屏幕上的影像中的向上的方向。试想，如果仅仅确定了视点和观察点，观察者还是可能以视线为轴旋转的（如下图所示，头部偏移会导致观察到的场景也偏移了）。所以，为了将观察者固定住，我们还需要指定上方向。上方向是具有3个分量的矢量，用（upX，upY，upZ）表示。

在WebGL中，我们可以用上述三个矢量创建一个视图矩阵（view matrix），然后将该矩阵传给顶点着色器。视图矩阵可以表示观察者的状态，含有观察者的视点、观察目标点、上方向等信息。之所以被称为视图矩阵，是因为它最终影响了显示在屏幕上的视图，也就是观察者观察到的场景。根据提供的Matrix4.setLookAt（）函数可以根据上述三个矢量：视点、观察点和上方向，来创建出视图矩阵 （矩阵库 WebGL矩阵变换库_山楂树の的博客-CSDN博客）。 

在WebGL中，观察者的默认状态应该是这样的：

● 视点位于坐标系统原点（0，0，0）。

● 视线为Z轴负方向，观察点为（0，0，-1）

如果将上方向改为X轴正半轴方向（1，0，0），你将看到场景旋转了90度。

创建这样一个矩阵，你只需要简单地使用如下代码（见下图）。

现在，你已经了解了setLookAt（）函数，下面来看示例程序的代码。

视图矩阵程序（LookAtTriangles.js） 

程序显示了LookAtTriangles.js的代码，我们修改了视点，然后绘制了3个三角形，如上图三角形所示。实际上这3个三角形的颜色分别为蓝色到红色、黄色到红色和绿色到红色的渐变色。

var VSHADER_SOURCE =
  'attribute vec4 a_Position;\n' +
  'attribute vec4 a_Color;\n' +
  'uniform mat4 u_ViewMatrix;\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_Position = u_ViewMatrix * a_Position;\n' +
  '  v_Color = a_Color;\n' +
  '}\n';

var FSHADER_SOURCE =
  '#ifdef GL_ES\n' +
  'precision mediump float;\n' +
  '#endif\n' +
  'varying vec4 v_Color;\n' +
  'void main() {\n' +
  '  gl_FragColor = v_Color;\n' +
  '}\n';

function main() {
  var canvas = document.getElementById('webgl');
  var gl = getWebGLContext(canvas);
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('Failed to intialize shaders.');
    return;
  }
  // 设置顶点坐标和颜色（蓝色三角形在最前面）
  var n = initVertexBuffers(gl);
  gl.clearColor(0, 0, 0, 1);
  // 获取u_ViewMatrix变量的存储地址
  var u_ViewMatrix = gl.getUniformLocation(gl.program, 'u_ViewMatrix');
  // 设置视点、视线和上方向
  var viewMatrix = new Matrix4();
  viewMatrix.setLookAt(0.20, 0.25, 0.25, 0, 0, 0, 0, 1, 0);
  // 将视图矩阵传给u_ViewMatrix变量
  gl.uniformMatrix4fv(u_ViewMatrix, false, viewMatrix.elements);
  gl.clear(gl.COLOR_BUFFER_BIT);
  // 绘制三角形
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffers(gl) {
  var verticesColors = new Float32Array([
    // 顶点和坐标颜色
     0.0,  0.5,  -0.4,  0.4,  1.0,  0.4, // 绿色三角形在最后面
    -0.5, -0.5,  -0.4,  0.4,  1.0,  0.4,
     0.5, -0.5,  -0.4,  1.0,  0.4,  0.4, 
     0.5,  0.4,  -0.2,  1.0,  0.4,  0.4, // 黄色三角形在中间
    -0.5,  0.4,  -0.2,  1.0,  1.0,  0.4,
     0.0, -0.6,  -0.2,  1.0,  1.0,  0.4, 
     0.0,  0.5,   0.0,  0.4,  0.4,  1.0,  // 蓝色三角形在最前面
    -0.5, -0.5,   0.0,  0.4,  0.4,  1.0,
     0.5, -0.5,   0.0,  1.0,  0.4,  0.4, 
  ]);
  var n = 9;
  // 创建缓冲区对象
  var vertexColorbuffer = gl.createBuffer();  
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexColorbuffer);
  gl.bufferData(gl.ARRAY_BUFFER, verticesColors, gl.STATIC_DRAW);
  var FSIZE = verticesColors.BYTES_PER_ELEMENT;
  var a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  gl.vertexAttribPointer(a_Position, 3, gl.FLOAT, false, FSIZE * 6, 0);
  gl.enableVertexAttribArray(a_Position);
  var a_Color = gl.getAttribLocation(gl.program, 'a_Color');
  gl.vertexAttribPointer(a_Color, 3, gl.FLOAT, false, FSIZE * 6, FSIZE * 3);
  gl.enableVertexAttribArray(a_Color);
  gl.bindBuffer(gl.ARRAY_BUFFER, null);
  return n;
}

首先，来看一下initVertexBuffers（）函数（第42行）。verticesColors数组包含了3个三角形共计9个顶点的数据，而且顶点坐标的z分量也不再是0了。接着我们创建了缓冲区对象（第57行），并将数组中的数据填了进去（第58～59行）。此外，我们还把gl.drawArrays（）的第3个参数改成了9（第39行），因为这里共有9个顶点。

然后，需要建立视图矩阵（包含了视点、视线和上方向信息）并传给顶点着色器。为此，我们先创建了一个Matrix4对象viewMatrix（第33行），然后用setLookAt（）方法将其设置为视图矩阵（第34行），最后将视图矩阵中的元素传给顶点着色器中的u_ViewMatrix变量（第36行）。

 实际上，“根据自定义的观察者状态，绘制观察者看到的景象”与“使用默认的观察状态，但是对三维对象进行平移、旋转等变换，再绘制观察者看到的景象”，这两种行为是等价的。（归根结底：不论视图怎样变化，无疑就是旋转、平移等操作，最终本质上都是对物体进行相反方向的旋转平移（默认的视角））

举个例子，默认情况下视点在原点，视线沿着Z轴负方向进行观察。假如我们将视点移动到（0，0，1），如下图（左）所示。这时，视点与被观察的三角形在Z轴上的距离增加了1.0个单位。实际上，如果我们使三角形沿Z轴负方向移动1.0个单位，也可以达到同样的效果，因为观察者看上去是一样的，如下图（右）所示。

移动视点和移动被观察对象等效

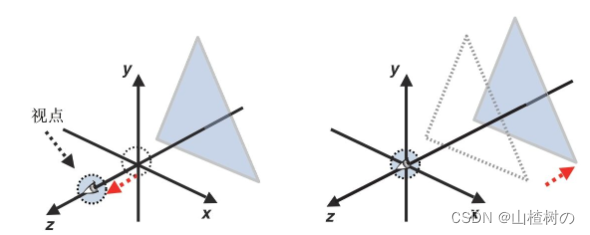
事实上，上述过程就发生在示例程序LookAtTriangles.js中。根据视点、观察点和上方向参数，setLookAt（）方法计算出的视图矩阵恰恰就是“沿着Z轴负方向移动1.0个单位”的变换矩阵。所以，把这个矩阵与顶点坐标相乘，就相当于获得了“将视点设置在（0.0，0.0，1.0）”的效果。视点移动的方向与被观察对象（也就是整个世界）移动的方向正好相反。对于视点的旋转，也可以采用类似的方式。 

“改变观察者的状态”与“对整个世界进行平移和旋转变换”，本质上是一样的，它们都可以用矩阵来描述。接下来，我们将从一个指定的视点来观察旋转后的三角形。

从指定视点观察旋转后的三角形

现在将修改LookAtTriangles程序来绘制一个从指定位置看过去的旋转后的三角形。这时，我们需要两个矩阵：旋转矩阵（表示三角形的旋转）和视图矩阵（表示观察世界的方式）。首先有一个问题是，以怎样的顺序相乘这两个矩阵。

我们知道，矩阵乘以顶点坐标，得到的结果是顶点经过矩阵变换之后的新坐标。也就是说，用旋转矩阵乘以顶点坐标，就可以得到旋转后的顶点坐标。

用视图矩阵乘以顶点坐标会把顶点变换到合适的位置，使得观察者（以默认状态）观察新位置的顶点，就好像在观察者处在（视图矩阵描述的）视点上观察原始顶点一样。现在要在某个视点处观察旋转后的三角形，我们需要先旋转三角形，然后从这个视点来观察它。换句话说，我们需要先对三角形进行旋转变换，再对旋转后的三角形进行与“移动视点”等效的变换。我们按照上述顺序相乘两个矩阵。具体看一下等式。

我们知道，如果想旋转图形，就需要用旋转矩阵乘以旋转前的顶点坐标：

＜旋转后顶点坐标＞=＜旋转矩阵＞×＜原始顶点坐标＞

用视图矩阵乘以旋转后的顶点坐标，就可以获得“从视点看上去”的旋转后的顶点坐标： 

＜“从视点看上去”的旋转后顶点坐标＞=＜视图矩阵＞×＜旋转后顶点坐标＞

将第1个式子代入第2个，可得：

＜“从视点看上去”的旋转后顶点坐标＞=＜视图矩阵＞×＜旋转矩阵＞×＜原始顶点坐标＞

除了旋转矩阵，你还可以使用平移、缩放等基本变换矩阵或它们的组合，这时矩阵被称为模型矩阵（model matrix）。这样，上式就可以写成：

＜视图矩阵＞×＜模型矩阵＞×＜原始顶点坐标＞

示例程序在着色器中实现了该式。很简单，直接照着该式修改顶点着色器。修改后的LootAtRotatedTriangles程序实现了上述变换，如下图所示。图中白色虚线为旋转前三角形的所在位置，可以看到三角形确实被旋转过了。

模型视图矩阵程序（LookAtRotatedTriangles.js） 

LookAtRotatedTriangles.js与LookAtTriangles.js相比，只有几处小改动：加入了uniform变量u_ModelMatrix；JavaScript中的main（）函数将模型矩阵传给该变量。相应的代码如下所示。

首先，顶点着色器中添加了uniform变量u_ModelMatrix（第7行），该变量从JavaScript中接收模型矩阵，以实现等式＜视图矩阵＞×＜模型矩阵＞×＜原始顶点坐标＞。 

JavaScript的main（）函数已经有了与视图矩阵相关的代码，只需添加几行计算和传入旋转矩阵的代码，将三角形绕Z轴旋转10度。第53行代码实现了获取u_ModelMatrix变量的存储地址，第64行实现了创建一个新的矩阵对象modelMatrix，调用Matrix.setRotate（）将其设为旋转矩阵（第65行），然后传给顶点着色器中的u_ModelMatrix（第69行）。

运行示例程序，顶点坐标依次与旋转矩阵和视图矩阵相乘，最终获得了预期的效果。如上图所示，即先用u_ModelMatrix旋转三角形，再将旋转后的坐标用u_ViewMatrix变换到正确的位置，使其看上去就像是从指定视点处观察一样。

模型视图矩阵

在LookAtRotatedTriangle.js中，着色器实现了式（视图矩阵×模型矩阵×原始坐标）。这样，程序对每个顶点都要计算视图矩阵×模型矩阵。如果顶点数量很多，这一步操作就会造成不必要的开销。这是因为，无论对哪个顶点而言，式（视图矩阵×模型矩阵×原始坐标）中的两个矩阵相乘的结果都是一样的。所以我们可以在JavaScript中事先把这两个矩阵相乘的结果计算出来，再传给顶点着色器。这两个矩阵相乘得到的结果被称为模型视图矩阵（model view matrix），如下所示：

＜模型视图矩阵＞=＜视图矩阵＞×＜模型矩阵＞

式视图矩阵×模型矩阵×原始坐标可以重写为下式

＜模型视图矩阵＞×＜顶点坐标＞

新的示例程序LookAtRotatedTriangles_mvMatrix.js按照式＜模型视图矩阵＞×＜顶点坐标＞重写了LookAtRotatedTriangles中的代码，如下所示。

顶点着色器中出现了新的uniform变量u_mvMatrix，它参与了对gl_Position的计算（第9行）。顶点着色器执行的流程与最初的LookAtTriangles.js中一样（除了uniform变量的名称）。

在JavaScript代码中，我们分别计算出了视图矩阵viewMatrix和模型矩阵modelMatrix（第59～63行），就像在LookAtTriangle.js中一样。然后，我们调用Matrix4.multiply（）方法使这两个矩阵相乘，并将结果赋值给modelviewMatrix（第66行）。注意，我们是在viewMatrix上调用了multiply（）方法，并传入modelMatrix为参数，所以这样做的结果实际上就是modelViewMatrix=viewMatrix＊modelMatrix。因为在JavaScript中，我们不能像在GLSL ES中那样直接使用＊号来进行矩阵相乘，而需要用矩阵库所提供的方法。 

得到了modelViewMatrix后，就将它传给着色器的u_ModelMatrix变量（第69行）。运行程序，效果如下图所示。

最后还需要指出，示例程序显式地把视图矩阵和模型矩阵单独计算出来，再相乘为模型视图矩阵（第59～66行），是为了更好地表达模型视图矩阵的由来。实际上，只需要一行代码就可以计算出模型视图矩阵了：（计算出视图矩阵，再将视图矩阵与模型矩阵(当前只有旋转)相乘）