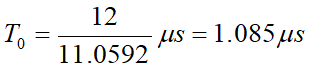【DELM回归预测】基于matlab粒子群算法改进深度学习极限学习机PSO-DELM数据回归预测【含Matlab源码 1884期】

⛄一、PSO-DELM简介

1 DELM的原理
在2004年，极限学习机（extreme learning machine,ELM）理论被南洋理工大学的黄广斌教授提出，ELM是一种单隐含层前馈神经网络（single-hidden layer feedforward neural network,SLFN）算法。它与常用的BP神经网络相比，ELM是对于权重和阈值随机的选取，而不像BP是通过反向传播算法调节各层之间的权值和阈值，从而减少了算法模型的学习时间和结构的复杂性，提高了模型整体的训练速度。

ELM的基本结构如图1所示，其由输入层、隐含层、输出层这3部分组成。原理说明如下，假设输入数据的样本集合为：X=xi|{1≤i≤N}，输出数据的样本集合为：Y=yi|{1≤i≤N}，其中N为样本总个数、xi为输入样本的第i个训练样本、yi为输出样本的第i个输出样本。这里设置隐含层的神经元个数为J个，则H={hi|1≤i≤J}为隐含层的输出向量的集合，hi为第i个输入样本对应的特征向量。把输入的样本数据在空间上映射到隐含层特征空间上，其二者的关系为
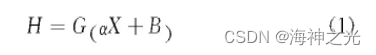
在这里插入图片描述
式中：G为激活函数，主要应用的有Sigmoid、Sin、Hardlim等等；α为输入层各个节点到隐含层各个节点的输入权重矩阵；B为隐含层各个节点的阈值矩阵。

图1 ELM的结构
若单隐含层的ELM能够实现在误差极小的情况下逼近“输出的N个样本”，则隐含层的输出为
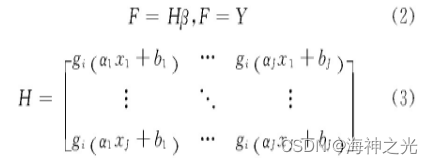
在这里插入图片描述
式中：β为隐含层各个节点到输出层各个节点的输出权重矩阵；H为隐含层输出矩阵。

从以上说明中能看出极限学习机的目的就是让模型的输出与实际的输出之间的差值最小，即求解输出权重矩阵的最小二乘解的问题，只要模型能够输出权重矩阵的最小二乘解就可以完成模型的训练，输出权重矩阵β可由下式表示为
在这里插入图片描述
式中：H+为隐含层输出矩阵H的Moore-Penrose广义矩阵。

由于ELM为单隐含层结构，在面对数据量过大、输入数据的维度过高的输入输出变量时，单隐含层的极限学习机无法捕捉到数据的有效特征。在ELM中的权重和阈值是随机的产生的，这可能会使得部分的神经元成为无效的神经元，减弱算法模型对数据特征的学习能力。在研究中发现，更多的学者对于ELM的衍生算法深度极限学习机（deep extreme learning machine,DELM）产生了浓厚的兴趣，所以本文提出使用DELM对数据分析，弥补了ELM的缺点。为了增强模型的泛化能力，这里选择加入一个正则化项
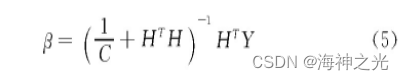
在这里插入图片描述
式中：C为正则化系数。

本文在构建深度极限学习机中采用ELM自动编码器（ELM autoencoder,ELM-AE）算法得到模型的权值和阈值，ELM-AE的结构如图2所示。自动编码器（auto encoder,AE）是以无监督的学习方式学习数据的特征，它是将输入的向量通过编码器映射到隐含层的特征向量，再由解码器将特征向量重新构造原来的输入向量。构建的ELM-AE使得隐含层节点随机权值和随机阈值正交，如果随机权重和随机阈值不是正交的，它也是能够有一个很好的特征表示作用，从而提高ELM-AE的泛化能力。在ELM-AE产生正交的随机权重和阈值为
在这里插入图片描述
式中：I是单位矩阵。

图2 ELM-AE结构
在ELM-AE中，输出权重β负责学习从特征空间到输入数据的转换。并且在传统的方法中，是根据最小二乘法求得权重系数，但是在隐含层节点数过多的情况下，这样会导致模型的泛化能力弱和鲁棒性差。所以在求解权重系数中引入正则化系数，提高模型的泛化能力，这里将目标函数设置为
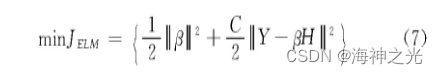
在这里插入图片描述
式中：C为正则化参数。对于稀疏和压缩的ELM-AE表示，把公式中的β求导，并且让目标函数为0，这样求得输出权重β为

式中：H为ELM-AE的隐含层输出矩阵；X为ELM-AE的输入和输出。

对于输入维度等于编码维度的ELM-AE,ELM-AE的输出权重矩阵β代表着从输入特征空间的数据到隐含层特征空间的转换，则输出权重β的计算公式为
在这里插入图片描述
并且在DELM中ELM-AE能用奇异值（SVD）来表示其特征，所以式（5）的奇异值分解为

式中：u是HTH的特征向量；di是H的奇异值。

深度极限学习机从结构上看相当于把多个ELM连接到了一起，但它相对于ELM能更全面地捕捉到数据之间的映射关系并提高处理高维度输入变量的精确度。DELM是逐层通过ELM-AE进行无监督的训练学习，最后接入回归层进行监督训练。其DELM的结构如图3所示，假设模型有M个隐含层，将输入数据样本X根据ELM-AE理论得到第一个权重矩阵β1，接着得到隐含层的特征向量H1。以此类推，能够得到M层的输入权重矩阵βM和隐含层的特征向量HM。并且模型的前期是进行多层无监督的学习，不需要人为设置输入的权重和阈值，只要设置各层的隐含层的神经元个数，所以DELM拥有的学习过程快且泛化能力强的特点。
在这里插入图片描述
图3 DELM结构

2 粒子群算法优化深度极限学习机
2.1 粒子群算法原理
粒子群算法（partile swarm optimization,PSO）是由Kennedy和Eberhart提出的一种随机优化算法。它的提出是通过对鸟类等生物有机体的社会行为进行模拟。PSO的原理如下：把假设的目标值区域当成鸟类等生物的捕食区域，生物在搜捕猎物的过程可以比作是粒子在不断更新着搜索目标值所在区域，生物在捕食的开始是有一个大概的方向，相当于粒子在搜索过程中有一个初始的速度和位移，这个过程就是粒子的寻优过程。在算法中模拟的随机粒子是通过两个极值点来更新自己，保证粒子在搜索过程中能确定最接近目标值区域的粒子范围。第一个极值点就是随机粒子中的拥有最佳位置的个体极值（Pbest），第二个极值点就是种群中拥有最佳位置的个体极值点（Gbest）。在D维空间上第i个粒子的速度和位置分别是
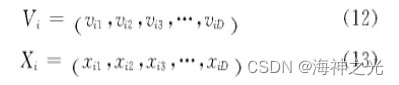
在这里插入图片描述
在每次的迭代过程中，根据两个极值点Pbest和Gbest的位置更新，逐渐找到种群中粒子的最佳位置，其中更新的公式为

2.2 优化过程
由于DELM的中各个隐含层的神经元个数需要人为的设置，并且隐含层的神经元个数一般设置的较大才能使模型在做回归预测时的精度提高，在设置的过程中学者要通过大量的数据和仿真实验来验证隐含层神经元个数的取值，从而保证模型的误差函数最小。又因为随着隐含层神经元个数的增多，每次进行仿真实验验证的神经元个数的上下波动范围较大，造成实验的过程过于复杂和使模型具有不确定性。本文采用粒子群优化算法对多个隐含层的个数选取，经过优化找到各个隐含层最优的神经元个数赋值给算法模型。PSO相对于其它的优化算法具有：收敛速度快、效率高、算法简单和扩展空间的特点。

使用PSO优化DELM的好处有：(1)减少对多个隐含层的神经元个数选择的仿真实验。(2)优化算法并不复杂，不会导致模型的优化时间过长，并且能提高预测精度。(3)优化后的模型有更好的鲁棒性。

粒子群算法优化深度极限学习机的具体步骤，流程如图4所示：

步骤1把数据划分为训练集合预测集。

步骤2对PSO的参数初始化（w、c1、c2）。

步骤3确定DELM的拓扑结构，以及相关参数的设置。

步骤4将DELM训练测试得到的均方误差作为PSO的适应度值。

步骤5初始最优解更新（Pbest、Gbest），通过种群移动（更新粒子位置和速度）、计算新的适应度值、更新当前的最优解看是否满足适应度值。若不满足，则重新进行迭代。

步骤6把获得的各隐含层的最优节点数代入DELM中。

步骤7训练测试。

步骤8得到预测结果。
在这里插入图片描述
图4 流程

⛄二、部分源代码

clear;clc;close all;
%% 导入数据
load data
%训练集——400个样本
P_train=input(:,(1:550));
T_train=output((1:550));
% 测试集——200个样本
P_test=input(:,(250:350));
T_test=output((250:350));
%% 归一化
% 训练集
[Pn_train,inputps] = mapminmax(P_train,0,1);
Pn_test = mapminmax(‘apply’,P_test,inputps);
% 测试集
[Tn_train,outputps] = mapminmax(T_train,0,1);
Tn_test = mapminmax(‘apply’,T_test,outputps);

%所有的数据输入类型应该为 N*dim，其中N为数据组数，dim为数据的维度
Pn_train = Pn_train’;
Pn_test = Pn_test’;
Tn_train = Tn_train’;
Tn_test = Tn_test’;

%% DELM参数设置
ELMAEhiddenLayer = [2,3];%ELM—AE的隐藏层数，[n1,n2,…,n],n1代表第1个隐藏层的节点数。
ActivF = ‘sig’;%ELM-AE的激活函数设置
C = inf; %正则化系数
%% 优化算法参数设置：
%计算权值的维度
dim = ELMAEhiddenLayer(1)*size(Pn_train,2);
if length(ELMAEhiddenLayer)>1
for i = 2:length(ELMAEhiddenLayer)
dim = dim + ELMAEhiddenLayer(i)*ELMAEhiddenLayer(i-1);
end
end
popsize = 20;%种群数量
Max_iteration = 50;%最大迭代次数
lb = -1;%权值下边界
ub = 1;%权值上边界

fobj = @(X)fun(X,Pn_train,Tn_train,Pn_test,Tn_test,ELMAEhiddenLayer,ActivF,C);
[Best_pos,Best_score,PSO_cg_curve]=PSO(popsize,Max_iteration,lb,ub,dim,fobj);
figure
plot(PSO_cg_curve,‘k’,‘linewidth’,2)
xlabel(‘迭代次数’)
ylabel(‘适应度值’)
grid on
title(‘粒子群算法收敛曲线’)
%% 利用粒子群获得的初始权重，进行训练
BestWeitht = Best_pos;
%DELM训练
OutWeight = DELMTrainWithInitial(BestWeitht,Pn_train,Tn_train,ELMAEhiddenLayer,ActivF,C);
%训练集测试结果
predictValueTrainPSO = DELMPredict(Pn_train,OutWeight,ELMAEhiddenLayer);
% 反归一化
predictValueTrainPSO = mapminmax(‘reverse’,predictValueTrainPSO,outputps);
% 均方误差
Error1PSO = (predictValueTrainPSO’ - T_train);
MSE1PSO = mse(Error1PSO);
%测试集测试结果
predictValueTestPSO = DELMPredict(Pn_test,OutWeight,ELMAEhiddenLayer);
% 反归一化
predictValueTestPSO = mapminmax(‘reverse’,predictValueTestPSO,outputps);
% 均方误差
Error2PSO = (predictValueTestPSO’ - T_test);
MSE2PSO = mse(Error2PSO);