目录

1 梯度弥散、梯度爆炸的成因

2  解决方式

2.1.pretrain+finetune

2.2 梯度裁剪

2.3 权重正则化

2.5 Batch Normalization正则化

2.6 残差结构 shortcut

2.7 LSTM

---

1 梯度弥散、梯度爆炸的成因

神经网络的层（主要是隐藏层）越多，对输入特征抽象层次越高。因为在神经网络中，后一层神经元的输入是前一层输出的加权和，前一层的特征在后一层就被抽象出来了，学习的过程其实就是调节和优化各连接权重和阈值的过程。

理论上层数越多，效果越好。然而实际上，盲目不停地增加层数，则会容易引起overfitting，从而导致预测效果不好，所以并不是层数越多，预测效果就一定会越好的。

简单地增加深度，会导致梯度弥散（梯度消失）或梯度爆炸。

梯度消失：随着深度增加，梯度急剧减小。梯度消失是指在反向传播过程中梯度逐渐降低到0导致参数不可学习的情况。最后几层可以改变，但前几层（靠近输入层的隐含层神经元）相对固定，变为浅层模型，不能有效地学习。很大程度上是来自于激活函数的饱和。

原因：根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话，那么即使这个结果是0.99，在经过足够多层传播之后，误差对输入层的偏导会趋于0。

梯度爆炸：梯度消失相反，在反向传播过程中由于梯度过大导致模型无法收敛的情形。导致靠近输入层的隐含层神经元调整变动极大。

原因：根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都大于1的话，在经过足够多层传播之后，误差对输入层的偏导会趋于无穷大。

2  解决方式

2.1.pretrain+finetune

在预训练完成后，再对整个网络进行“微调”（fine-tunning），此思想相当于是先寻找局部最优，然后整合起来寻找全局最优。

2.2 梯度裁剪

主要是针对梯度爆炸提出的，其思想是设置一个梯度剪切阈值，然后更新梯度的时候，如果梯度超过这个阈值，那么就将其强制限制在这个范围之内，通过这种直接的方法就可以防止梯度爆炸。

2.3 权重正则化

L1正则：在损失函数里加入参数绝对值之和

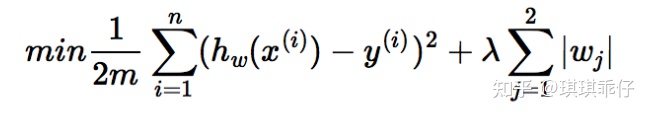
L2正则：在损失函数里加入参数的平方和

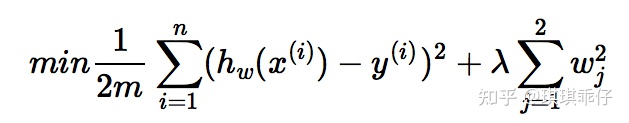
如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。事实上，在深度神经网络中，往往是梯度消失出现的更多一些。

2.4 ReLU、LeakReLU、ELU等激活函数 替换sigmoid

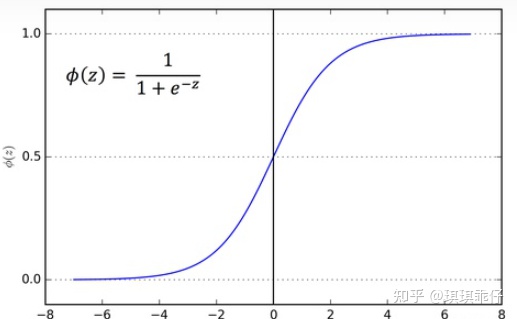
                                                         sigmoid激活函数

饱和神经元会使得梯度消失问题雪上加霜，假设神经元输入Sigmoid的值特别大或特别小，对应的梯度约等于0，即使从上一步传导来的梯度较大，该神经元权重(w)和偏置(bias)的梯度也会趋近于0，导致参数无法得到有效更新，使用梯度下降优化算法更新网络很慢。

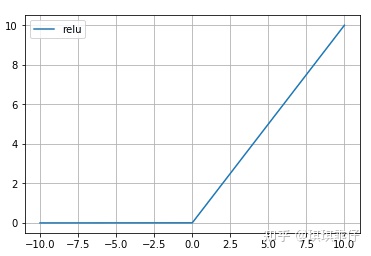
ReLU激活函数

ReLU激活函数成为了大多数神经网络的默认选择。①解决了梯度消失、爆炸的问题 ②计算方便，计算速度快 ③加速了网络的训练。同时也存在一些缺点：①由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）②输出不是以0为中心的

LeakyReLU激活函数

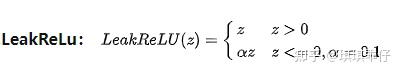
PReLU的α是用梯度下降学出来的

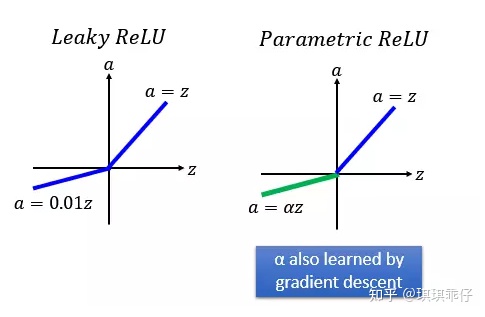
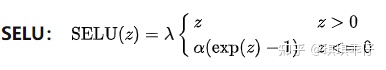
2.5 Batch Normalization正则化

Batch Normalization具有加速网络收敛速度，提升训练稳定性的效果，BN本质上是解决反向传播过程中的梯度问题。需要对数据做归一化，因为神经网络主要就是为了学习训练数据的分布，并在测试集上达到很好的泛化效果。但如果数据的分布一直在变，学习就很难了。BN 批规范化，就是为了解决分布变化问题。

需要BN的原因：一方面，如果每一个batch输入的数据都具有不同的分布，显然会给网络的训练带来困难。

另一方面，数据经过一层层网络计算后，其数据分布也在发生着变化，此现象称为Internal Covariate Shift（内部协变量偏移），会给下一层的网络学习带来困难。

Internal Covariate Shift：上一层网络的输出数据经过这一层网络计算后，数据的分布会发生变化，发生在神经网络的内部。和Covariate Shift，训练数据和测试数据存在分布的差异性不同。

BN是归一化的一种手段，极限来说，这种方式会减小图像之间的绝对差异，突出相对差异，加快训练速度。

为什么不能直接对神经网络的每一层做归一化：

避免学到的特征分布被归一化，学不到数据的特征。因此要加入可训练的参数做归一化，实现BN。

BN applied to x over a mini-batch

其中引入了缩放变量γ和平移变量β。之前也说过如果直接做归一化不做其他处理，神经网络是学不到任何东西的，但是加入这两个参数后，事情就不一样了。为了保证模型的表达能力不因为规范化而下降。

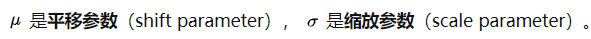
β是再平移参数，γ是再缩放参数。

优点：

1）没有它之前，需要小心的调整学习率和权重初始化，但是有了BN可以放心的使用大学习率，但是使用了BN，就不用小心的调参了，较大的学习率极大的提高了学习速度。

2）Batchnorm本身上是一种正则的方式，可以代替其他正则方式如dropout等

3）BN降低了数据之间的绝对差异，有一个去相关的性质，更多的考虑相对差异性，因此在分类任务上具有更好的效果。

（1）加快收敛速度：如果每层的数据分布都不一样的话，将会导致网络非常难收敛和训练，而如果把 每层的数据都在转换在均值为零，方差为1 的状态下，这样每层数据的分布都是一样的训练会比较容易收敛。

（2）防止梯度爆炸和梯度消失：以sigmoid为例，sigmoid函数使得输出在[0,1]之间。

(3) 防止过拟合：在网络的训练中，BN的使用使得一个minibatch中所有样本都被关联在了一起，因此网络不会从某一个训练样本中生成确定的结果，即同样一个样本的输出不再仅仅取决于样本的本身，也取决于跟这个样本同属一个batch的其他样本，而每次网络都是随机取batch，这样就会使得整个网络不会朝这一个方向使劲学习。一定程度上避免了过拟合。

为什么先BN 再ReLU（非线性激活层）--> BN+ReLU

2.6 残差结构 shortcut

接下来一讲 介绍 ResNet 等具有残差结构的经典网络。残差可以很轻松的构建几百层，一千多层的网络而不用担心梯度消失过快的问题，原因就在于残差的捷径（shortcut）部分。

2.7 LSTM

LSTM全称是长短期记忆网络（long-short term memory networks），是不那么容易发生梯度消失的，主要原因在于LSTM内部复杂的“门”(gates)，LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“，因此，经常用于生成文本中。