📖 前言:快考试了,做篇期末总结,都是重点与必考点。
博主预测考点:
计算题:RSA、Diffie-Hellman密钥交换、EIGamal 密钥交换、使用SHA-512算法,计算消息的Hash值、计算消息的HMAC
应用题:代替技术(1-2个)、置换技术、转轮机、分组密码、DES/AES的某一个环节
目录
- 🕒 1. 信息与网络安全概念
- 🕘 1.1 CIA
- 🕘 1.2 OSI 安全架构
- 🕘 1.3 安全攻击
- 🕤 1.3.1 被动攻击
- 🕤 1.3.2 主动攻击
- 🕘 1.4 网络安全模型
- 🕒 2. 传统加密技术
- 🕘 2.1 加密技术的发展
- 🕘 2.2 传统密码模型
- 🕘 2.3 密码编码学
- 🕤 2.3.1 特征
- 🕘 2.4 密码分析学与穷举攻击
- 🕘 2.5 攻击类型
- 🕘 2.6 代替技术 ☆☆☆
- 🕤 2.6.1 Caesar 密码
- 🕤 2.6.2 单表代替密码
- 🕤 2.6.3 多字母代替密码(Playfair密码)
- 🕤 2.6.4 多表代替加密(Vigenère密码)
- 🕤 2.6.5 多表代替加密(Vernam密码)
- 🕤 2.6.6 一次一密
- 🕘 2.7 置换技术 ☆☆☆
- 🕤 2.7.1 栅栏技术
- 🕤 2.7.2 多步置换
- 🕘 2.8 多层加密
- 🕤 2.8.1 转轮机 ☆☆☆
- 🕒 3. 分组密码和数据加密标准(DES)
- 🕘 3.1 分组密码
- 🕘 3.2 DES ☆☆☆
- 🕤 3.2.1 初始置换(IP)
- 🕤 3.2.2 16轮处理
- 🕤 3.2.3 轮函数(F)
- 🕞 3.2.3.1 扩展置换(E)
- 🕞 3.2.3.2 异或XOR(⊕)
- 🕞 3.2.3.3 S盒置换
- 🕞 3.2.3.4 P盒置换
- 🕤 3.2.4 逆初始置换(IP^-1^)
- 🕤 3.2.5 密钥生成
- 🕞 3.2.5.1 置换选择1
- 🕞 3.2.5.2 循环左移
- 🕞 3.2.5.3 置换选择2
- 🕒 4. 高级加密标准(AES)
- 🕘 4.1 总体结构
- 🕤 4.1.1 明文分组处理
- 🕘 4.2 详细结构
- 🕤 4.2.1 AES的一轮加密
- 🕘 4.3 AES的变换函数
- 🕤 4.3.1 字节代替(Substitute bytes)
- 🕤 4.3.2 行移位(ShiftRows)
- 🕤 4.3.3 列混淆(MixColumns)
- 🕤 4.3.4 轮密钥加(AddRoundKey)
- 🕤 4.3.5 AES单轮输入
- 🕒 5. 分组加密的工作模式
- 🕘 5.1 电码本ECB
- 🕘 5.2 密文分组链接CBC
- 🕘 5.3 密文反馈CFB
- 🕘 5.4 输出反馈OFB
- 🕘 5.5 计数器模式CTR
- 🕒 6. 公钥密码学与RSA
- 🕘 6.1 组成
- 🕤 6.1.1 明文
- 🕤 6.1.2 加密算法
- 🕤 6.1.3 公钥
- 🕤 6.1.4 私钥
- 🕤 6.1.5 密文
- 🕤 6.1.6 解密算法
- 🕘 6.2 公钥加密
- 🕘 6.3 私钥加密
- 🕘 6.4 双重加密
- 🕘 6.5 RSA算法☆☆☆
- 🕒 7. 密钥管理和其他公钥体制
- 🕘 7.1 Diffie-Hellman 密钥交换
- 🕘 7.2 EIGamal 密钥交换
- 🕒 8. Hash 函数
- 🕘 8.1 Hash 函数的应用
- 🕤 8.1.1 消息认证
- 🕤 8.1.2 数字签名
- 🕘 8.2 安全需求
- 🕘 8.3 安全Hash算法
- 🕘 8.4 SHA-512
- 🕤 8.4.1 附加填充位(步骤1)
- 🕤 8.4.2 附加长度位(步骤2)
- 🕤 8.4.3 缓冲区初始化(步骤3)
- 🕤 8.4.4 分组处理(步骤4)
- 🕒 9. 消息认证码
- 🕘 9.1 消息认证函数
- 🕤 9.1.1 Hash
- 🕤 9.1.2 加密
- 🕤 9.1.3 MAC
- 🕘 9.2 基于Hash函数的MAC——HMAC
- 🕒 10. 数字签名
🕒 1. 信息与网络安全概念
🕘 1.1 CIA
安全的三个关键目标:CIA
- 保密性,信息没有出现非授权泄露;
- 完整性,信息没有出现非授权修改或破坏;
- 可用性,信息能够及时可靠地访问和使用。
🕘 1.2 OSI 安全架构
OSI安全架构主要关注安全攻击、安全机制和安全服务
- 安全攻击: 任何危及信息系统安全的行为。
- 安全机制: 检测、阻止、恢复的过程。
- 安全服务: 加强系统安全性的服务。
🕘 1.3 安全攻击
🕤 1.3.1 被动攻击
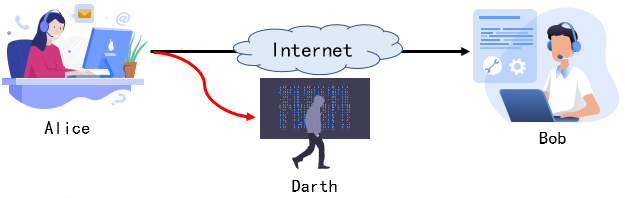
- 对传输进行窃听或监测,获取信息内容或流量模式
- 目的:获取传输的信息
- 两种被动攻击:信息内容泄露、流量分析
🕤 1.3.2 主动攻击
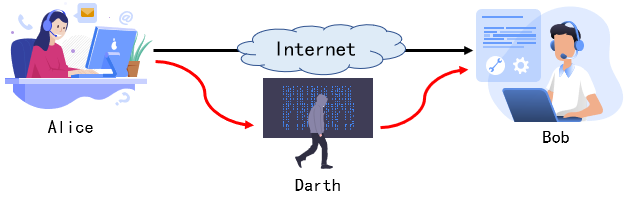
- 对数据流进行修改或伪造数据流
- 难以预防,只能检测后做到尽快恢复
分四类:伪装、重放、消息篡改和拒绝服务
-
消息篡改

-
重放
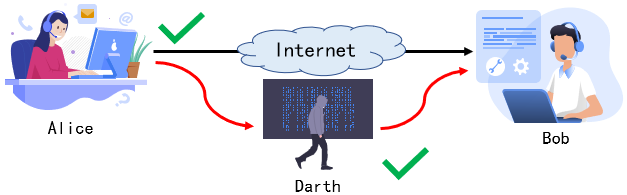
应用:Alice 传输认证信息给Bob ,告知Bob “我是Alice,代号0101,源IP为B”,Darth 截获该信息,获取了Alice代号。
Bob 收到信息后通过了Alice的认证
Darth 在认证后重发该信息“我是Alice,代号0101,IP为D”
Bob 通过认证,并认为这个IP也是Alice使用的
- 伪装
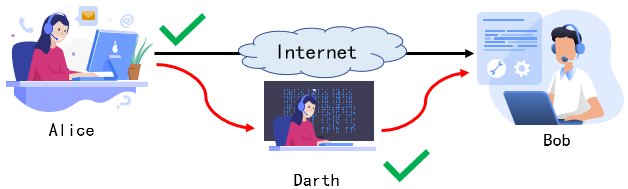
Darth 通过重放获取了Bob的认证信息,从而伪装成 Bob 传输信息给Alice 。
Alice 误以为接收到Bob的消息,实际来自Darth
- 拒绝服务
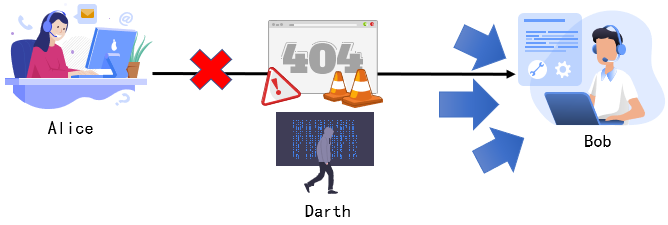
🕘 1.4 网络安全模型
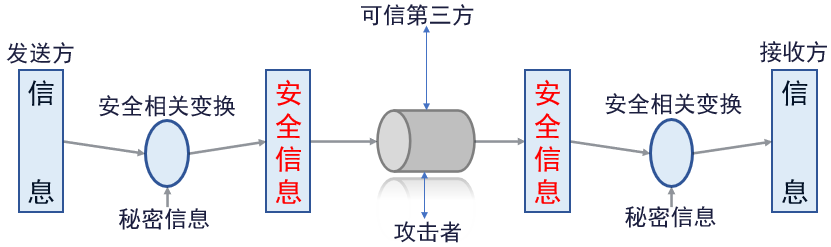
- 设计一个算法,它执行与安全相关的变换。该算法应是攻击者无法攻破的。
- 产生算法所使用的秘密信息。
- 设计分配和共享秘密信息的方法。
- 指明通信双方使用的协议,该协议利用安全算法和秘密信息实现安全服务。
🕒 2. 传统加密技术
🕘 2.1 加密技术的发展
- 传统加密:70年代前唯一的加密方法
- 对称加密:通信双方使用的密钥相同
- 单钥加密:加密、解密只涉及一个密钥
传统加密技术迄今仍广泛应用,DES、AES均在其中
🕘 2.2 传统密码模型
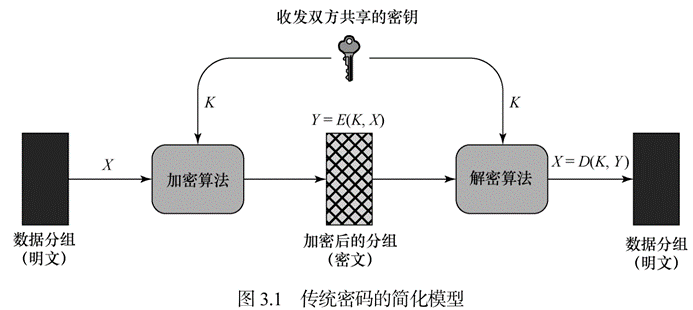
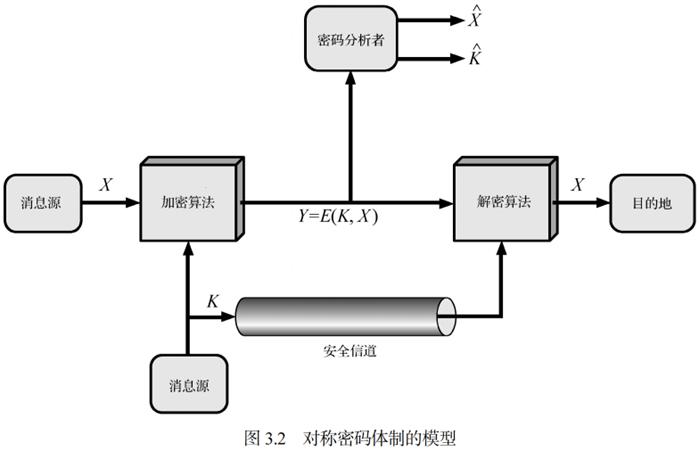
🕘 2.3 密码编码学
- 研究各种加密方案的领域 被称为密码编码学
- 研究的加密方案 被称为密码
🕤 2.3.1 特征
- 明文到密文的运算
所有的加密算法都基于两个原理:
- 代替:将明文中的每个元素映射成另一个元素,但顺序不变,如摩斯电码用—表示0
- 置换:将明文中的元素重新排列,明文字母保存不变,如栅栏技术
⌛ 大多数密码体制都是这两者的多重组合
- 所用的密钥数
-
相同密钥:通信双方使用相同的密钥,这种称为单钥密码、对称密码、传统密码,如DES、AES
-
不同密钥:通信双方使用不同的密钥,这种称为双钥密码、非对称密码、公钥密码,如RSA
- 处理明文
-
分组密码:加密算法一次处理一组元素,输出一组元素。典型的分组大小为64位或128位。(类似并行)
-
流密码:加密算法连续不断地处理元素,但一次只能处理一个元素,输出一个元素。元素可能是1字节,可能是1bit。(类似串行)
分组密码的应用范围比流密码要广泛
🕘 2.4 密码分析学与穷举攻击
- 密码分析学:利用算法的性质、明文的一般特征或某些明密文对。在缺少某些加密的细节情况下来推导特定的明文或使用的密钥。
- 穷举攻击:对一条密文尝试所有可能的密钥,直到把它转换为可读的、有意义的明文。平均而言,获得成功至少需要尝试所有可能密钥的一半。密钥的N种可能建立在已知明文类型的基础上
无论哪种方式,一旦推导出密钥,影响都将是灾难性的,过去、现在、未来所有使用该密钥加密的信息内容都出现了非授权泄露。
🕘 2.5 攻击类型
|
|
|
|---|---|
| 唯密文攻击 |
|
| 已知明文攻击 |
|
| 选择明文攻击 |
|
| 选择密文攻击 |
|
| 选择文本攻击 |
|
🕘 2.6 代替技术 ☆☆☆
🕤 2.6.1 Caesar 密码
Caesar密码是最早的代替密码,其加密原理非常简单,就是对字母表中的每个字母用它之后的第N个字母来代替
a
b
c
d
e
f
g
h
i
j
k
l
m
n
0
1
2
3
4
5
6
7
8
9
10
11
12
13
o
p
q
r
s
t
u
v
w
x
y
z
14
15
16
17
18
19
20
21
22
23
24
25
\begin{array}{l} \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{a} & \mathrm{b} & \mathrm{c} & \mathrm{d} & \mathrm{e} & \mathrm{f} & \mathrm{g} & \mathrm{h} & \mathrm{i} & \mathrm{j} & \mathrm{k} & \mathrm{l} & \mathrm{m} & \mathrm{n} \\ \hline 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline \end{array} \\ \\ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{o} & \mathrm{p} & \mathrm{q} & \mathrm{r} & \mathrm{s} & \mathrm{t} & \mathrm{u} & \mathrm{v} & \mathrm{w} & \mathrm{x} & \mathrm{y} & \mathrm{z} \\ \hline 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25 \\ \hline \end{array} \end{array}
a0b1c2d3e4f5g6h7i8j9k10l11m12n13o14p15q16r17s18t19u20v21w22x23y24z25
记住是从0开始!
练习题
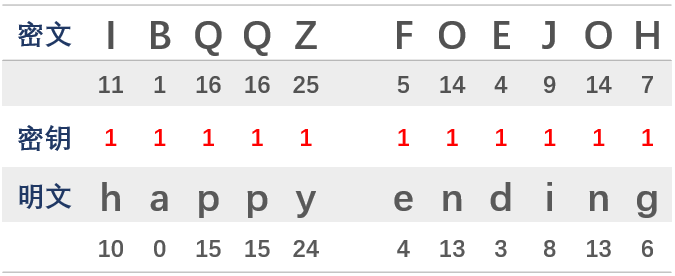
截获密文“IBQQZ FOEJOH”,已知使用Caesar加密,请恢复出明文。
【提示】密钥k在[1,3]之间
解答:当密钥 K = 1 :
还原出的明文具有实际意义,因此对应的明文为happy ending
若截获到一个用Caesar密码来加密的密文,那么参与加密运算E的密钥K只有25种可能,数量级很小,可以使用穷举攻击试出密钥K。
🕤 2.6.2 单表代替密码
对集合S内的所有元素进行排列,每个元素均出现且只出现一次,即全排列
若集合S 由n个元素组成,对S内的n个元素进行全排列
□□…□□□
第1位有n种选择,第2位有n-1种…以此类推,第n-1位有2种选择,第n位有1种选择,一共有n*(n-1)*(n-2)*.......*3*2*1种,即n!

即【明文字母表X】,通过指定【序号K】的【全排列】的变换,生成密文字母表Y
密钥K有26!种可能,远大于Caesar密码的密钥数量,可以抵挡对密钥K的穷举攻击
攻击:频率分析(可单/双字母分析)
🕤 2.6.3 多字母代替密码(Playfair密码)
Playfair密码是最早的多字母代替密码
规则:
- 从左到右2个2个地读取,当读取至相同字母时,则在它们之间
插入任意填充字母如x,继续读取 - 如果遇到明文为
奇数对,则在最后补位,如补x - 矩阵中没有字母
J,则明文中的J要被I代换。
加密:
- 同行用右边字母,同列用下边字母,异行异列(如下图)
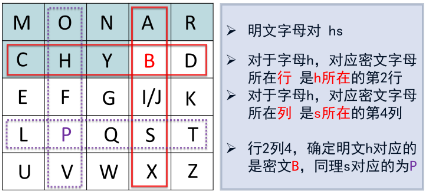
练习题
Alice和Bob选择“monarchy”作为Playfair加密的密钥词,请画出加密矩阵。并加密明文“balloon”
解答:处理明文:明文变为ba、lx、lo、on
密文:IB、SU、PM、NA
优点:一定程度隐藏了字母统计规律
缺点:仍可以做字母频率分析,相比单表代替密码难度大一点
🕤 2.6.4 多表代替加密(Vigenère密码)
a b c d e f g h i j k l m n 0 1 2 3 4 5 6 7 8 9 10 11 12 13 o p q r s t u v w x y z 14 15 16 17 18 19 20 21 22 23 24 25 \begin{array}{l} \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{a} & \mathrm{b} & \mathrm{c} & \mathrm{d} & \mathrm{e} & \mathrm{f} & \mathrm{g} & \mathrm{h} & \mathrm{i} & \mathrm{j} & \mathrm{k} & \mathrm{l} & \mathrm{m} & \mathrm{n} \\ \hline 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 \\ \hline \end{array} \\ \\ \begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline \mathrm{o} & \mathrm{p} & \mathrm{q} & \mathrm{r} & \mathrm{s} & \mathrm{t} & \mathrm{u} & \mathrm{v} & \mathrm{w} & \mathrm{x} & \mathrm{y} & \mathrm{z} \\ \hline 14 & 15 & 16 & 17 & 18 & 19 & 20 & 21 & 22 & 23 & 24 & 25 \\ \hline \end{array} \end{array} a0b1c2d3e4f5g6h7i8j9k10l11m12n13o14p15q16r17s18t19u20v21w22x23y24z25
练习题
Alice和Bob传递的明文为“happy”,约定用“hi”作为Vigenere加密的密钥词,请给出密文。
🕤 2.6.5 多表代替加密(Vernam密码)
练习题
使用Vernam密码加密信息“10 110 1110” ,对应的密钥流为 “00 100 1001”,请给出密文。
🕤 2.6.6 一次一密
使用与明文一样长、无重复、随机的密钥来加密消息,该密钥在解密消息后就丢弃不用
极度安全,很少使用
- 很难生产出超大规模的真正随机的字符
- 双方每发送一条信息就要依赖一个等长度的密钥来进行加解密,密钥的分配和保护困难。
🕘 2.7 置换技术 ☆☆☆
🕤 2.7.1 栅栏技术
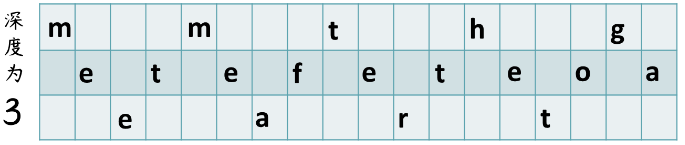
- 对角线的顺序写出明文
- 按行的顺序读出密文:MMTHG ETEFETEOA EART
🕤 2.7.2 多步置换
- 给定密钥共n位,将明文按一行n个排成矩阵
- 将明文依次填入矩阵,不足位选任意字母补齐(一般从z开始倒着写)
- 按对应列密钥次序读取生成密文
- 为达到更安全的目的,进行第2次置换
- 将1次置换生成的密文依次填入矩阵,按列读取
练习题
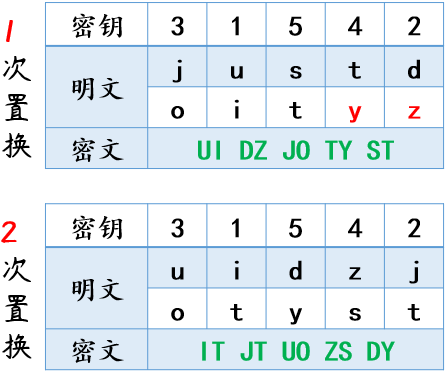
使用多步置换来加密信息“just do it”,密钥为31542,请给出二重置换后的密文。
🕘 2.8 多层加密
🕤 2.8.1 转轮机 ☆☆☆
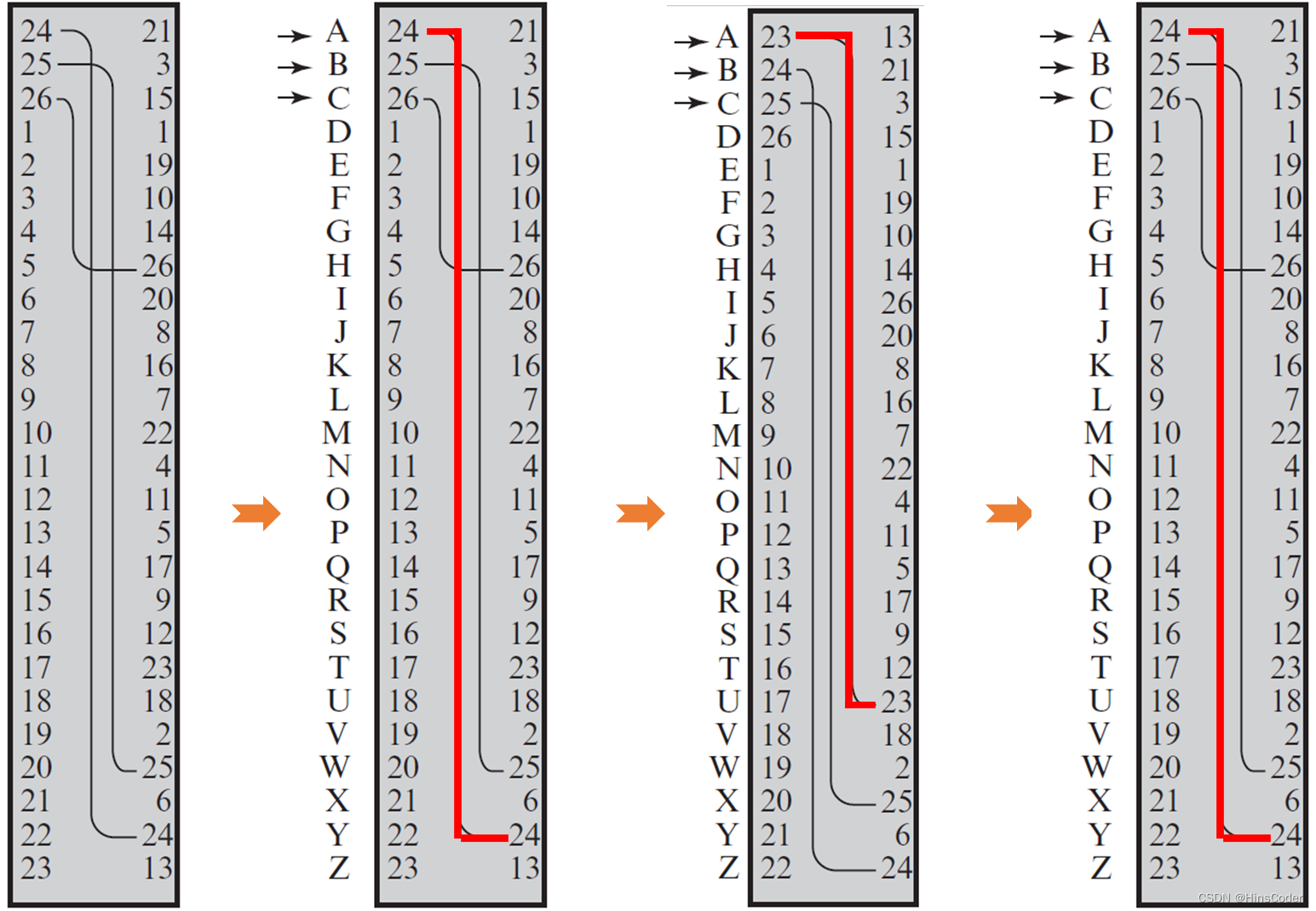
练习题
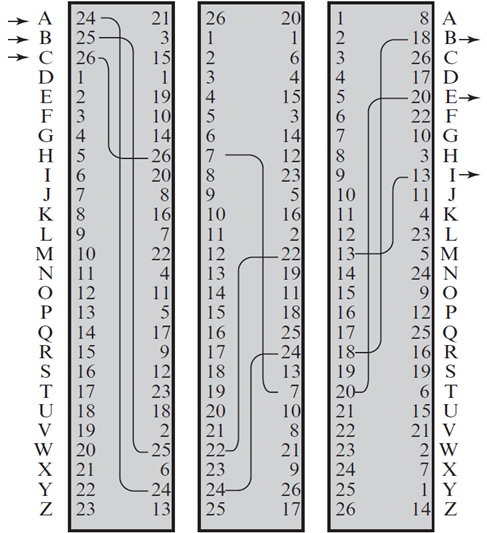
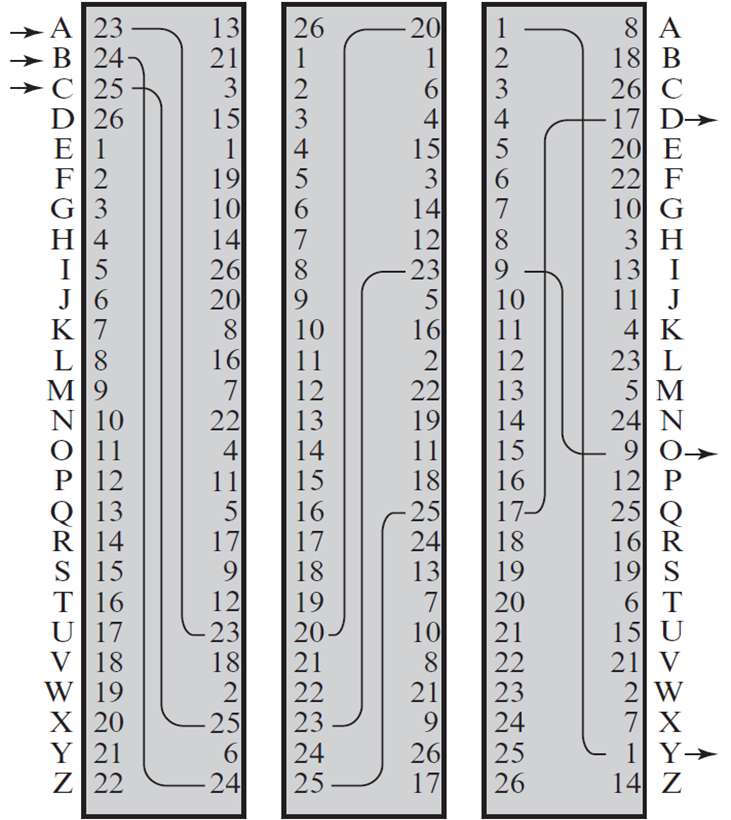
某转轮机构成如图所示。操作员按下字母b,经过三个圆筒处理后,分别变成了哪些字母?
操作员按下字母b后,第一个圆筒旋转1次,请画出旋转后的整个转轮机结构,无需标记内部连线。
解答:(1)B -> W -> M -> I
(2)
🕒 3. 分组密码和数据加密标准(DES)
🕘 3.1 分组密码
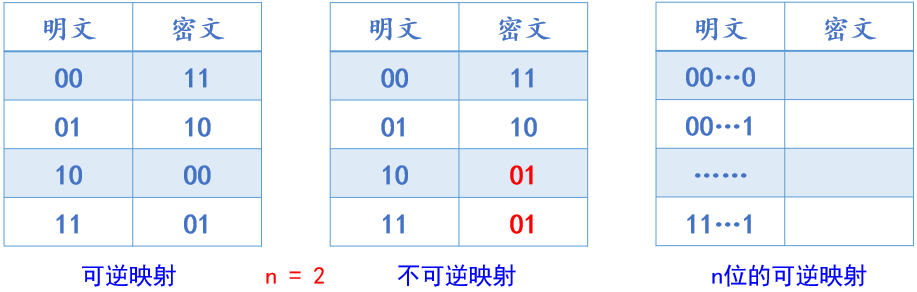
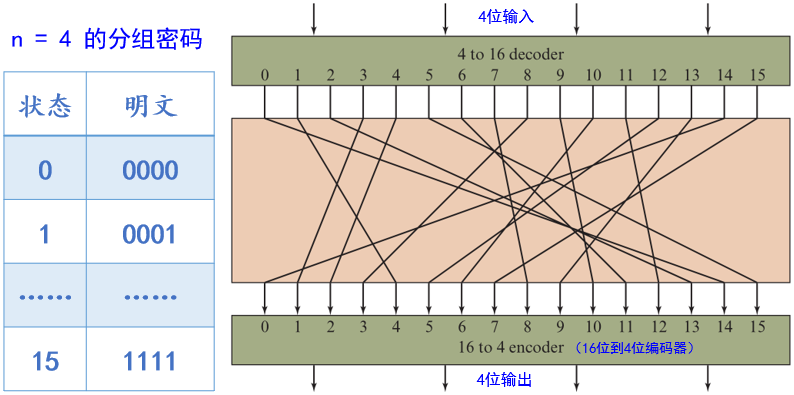
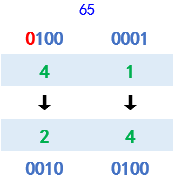
练习题:某4位分组密码的加密规则如上所示,请使用该密码加密大写字母A(ASCII值为65)。
解答:
将十进制65 转化为8位二进制数 0100 0001
- 第一组0100 :对应十进制为4,加密规则将4号输入状态转换为2号输出状态,对应二进制0010;
- 第二组0001 :对应十进制为1,加密规则将1号输入状态转换为4号输出状态,对应二进制0100;
因此密文为0010 0100,十进制为36
🕘 3.2 DES ☆☆☆
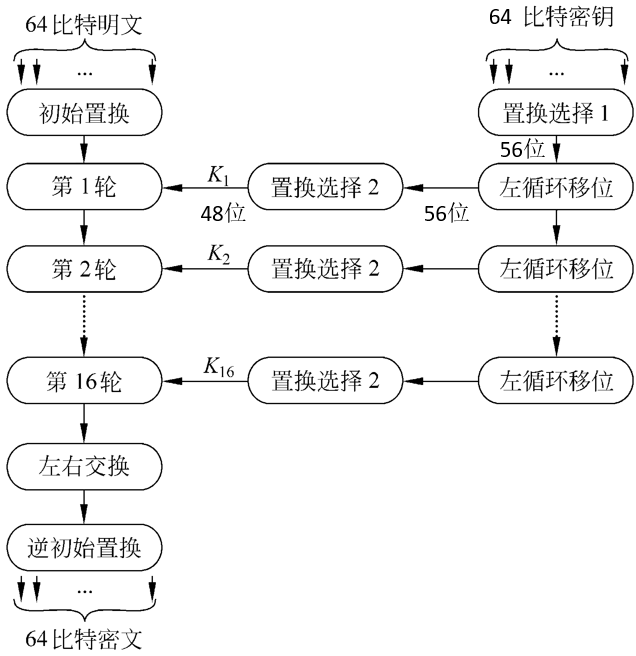
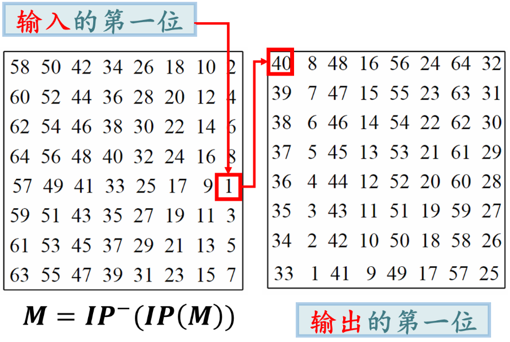
🕤 3.2.1 初始置换(IP)
64位明文分组按照置换表进行重排列,元素的位置发生改变,产生64位的输出
🕤 3.2.2 16轮处理
64位数据继续进行16轮处理,每轮都是相同的Feistel结构,最终产生64位输出
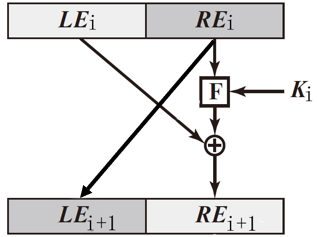
🕤 3.2.3 轮函数(F)
轮函数内部又包含4种变换,分别为扩展置换、XOR、S盒置换、P盒置换
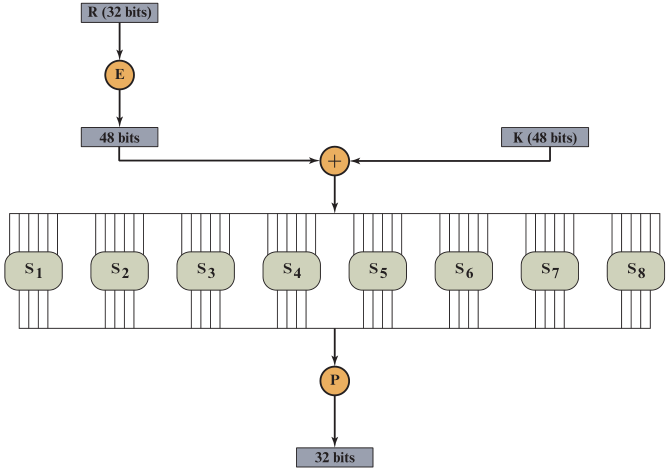
🕞 3.2.3.1 扩展置换(E)
将32位输入按扩展置换表扩展成为48位输出,使得扩展后数据长度与48位子密钥 等长
🕞 3.2.3.2 异或XOR(⊕)
将扩展置换生成的48位输出,与48位子密钥进行按位异或XOR
🕞 3.2.3.3 S盒置换
将48位输出每6位分成一组,每一组都通过S盒置换变为了4位
- 6位中取第
1位和第6位组成行号,剩余第2、3、4、5位组成列号 - 从S盒置换表中取出相应的十进制数,转化为4位二进制数
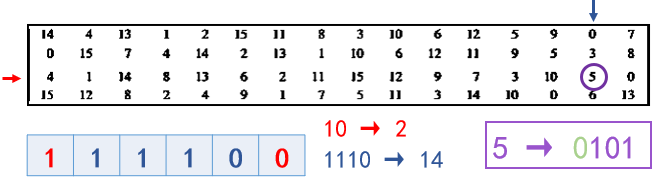
练习题
S盒的输入为111100,输出是什么?
14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13 \begin{array}{|rrrrrrrrrrrrrrrr|} \hline 14 & 4 & 13 & 1 & 2 & 15 & 11 & 8 & 3 & 10 & 6 & 12 & 5 & 9 & 0 & 7 \\ 0 & 15 & 7 & 4 & 14 & 2 & 13 & 1 & 10 & 6 & 12 & 11 & 9 & 5 & 3 & 8 \\ 4 & 1 & 14 & 8 & 13 & 6 & 2 & 11 & 15 & 12 & 9 & 7 & 3 & 10 & 5 & 0 \\ 15 & 12 & 8 & 2 & 4 & 9 & 1 & 7 & 5 & 11 & 3 & 14 & 10 & 0 & 6 & 13 \\ \hline \end{array} 1404154151121371481482214134152691113218111731015510612116129312117145931095100035678013
解答:
答案是0101
- 每个S盒的每一行都是整数
0到15的一个置换 - 改变S盒的任一输入比特,其输出至少有两比特发生改变
🕞 3.2.3.4 P盒置换
32位输出数据进行P盒置换,仍然输出为32位数据
🕤 3.2.4 逆初始置换(IP-1)
🕤 3.2.5 密钥生成
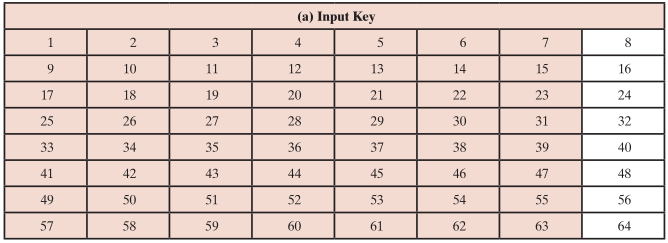
DES 提供了64位的密钥,但实际仅用到了其中的56位。
🕞 3.2.5.1 置换选择1
给64位密钥从1到64编号,忽略每个第8位,按照置换表进行选择与重新排列,产生56位的输出,分成两半:
C
0
,
D
0
C_0,D_0
C0,D0
C 0 57 49 41 33 25 17 9 1 58 50 42 34 26 18 10 2 59 51 43 35 27 19 11 3 60 52 44 36 D 0 63 55 47 39 31 23 15 7 62 54 46 38 30 22 14 6 61 53 45 37 29 21 13 5 28 20 12 4 \begin{array}{|llcccccc|} \hline C_{0} & 57 & 49 & 41 & 33 & 25 & 17 & 9 \\ & 1 & 58 & 50 & 42 & 34 & 26 & 18 \\ & 10 & 2 & 59 & 51 & 43 & 35 & 27 \\ & 19 & 11 & 3 & 60 & 52 & 44 & 36 \\ \hline D_{0} & 63 & 55 & 47 & 39 & 31 & 23 & 15 \\ & 7 & 62 & 54 & 46 & 38 & 30 & 22 \\ & 14 & 6 & 61 & 53 & 45 & 37 & 29 \\ & 21 & 13 & 5 & 28 & 20 & 12 & 4 \\ \hline \end{array} C0D057110196371421495821155626134150593475461533425160394653282534435231384520172635442330371291827361522294
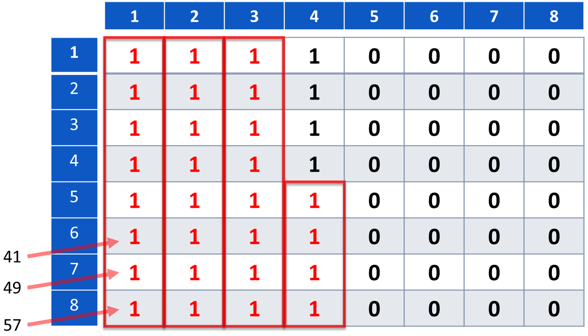
练习题
已知64位DES密钥如下,请给出进行置换选择1后的 C 0 C_0 C0。
1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 0 0 0 0 \begin{array}{|l|l|l|l|l|l|l|l|} \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline 1 & 1 & 1 & 1 & 0 & 0 & 0 & 0 \\ \hline \end{array} 1111111111111111111111111111111100000000000000000000000000000000
解答:
进行置换选择1后的 C 0 C_0 C0:
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 \begin{array}{|l|l|l|l|l|l|l|} \hline 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \hline 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \hline 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \hline 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \hline \end{array} 1111111111111111111111111111
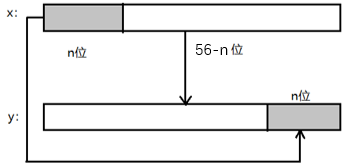
🕞 3.2.5.2 循环左移
56位密钥循环左移一次,产生56位的输出
迭代次数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 移位次数 1 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1 \begin{array}{|l|llllllllllllllll|} \hline \text { 迭代次数 } & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 \\ \hline \text { 移位次数 } & \color{Red} 1 &\color{Red} 1 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 1 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 2 &\color{Red} 1 \\ \hline \end{array} 迭代次数 移位次数 112132425262728291102112122132142152161
C 0 = 1111 0000110011001010101011 11 D 0 = 0101 0101011001100111100011 11 C 1 = 1110 0001100110010101010111 11 D 1 = 1010 1010110011001111000111 10 C 2 = 1100001100110010101010111111 D 2 = 0101010110011001111000111101 C 3 = 0000110011001010101011111111 D 3 = 0101011001100111100011110101 C 4 = 0011001100101010101111111100 D 4 = 0101100110011110001111010101 \begin{array}{l} C_{0}={\color{Red} 1111} 0000110011001010101011{\color{Red} 11} \\ D_{0}={\color{Red} 0101} 0101011001100111100011{\color{Red} 11} \\ C_{1}={\color{Red} 1110} 0001100110010101010111{\color{Red} 11} \\ D_{1}={\color{Red} 1010} 1010110011001111000111{\color{Red} 10} \\ C_{2}=1100001100110010101010111111 \\ D_{2}=0101010110011001111000111101 \\ C_{3}=0000110011001010101011111111 \\ D_{3}=0101011001100111100011110101 \\ C_{4}=0011001100101010101111111100 \\ D_{4}=0101100110011110001111010101 \end{array} C0=1111000011001100101010101111D0=0101010101100110011110001111C1=1110000110011001010101011111D1=1010101011001100111100011110C2=1100001100110010101010111111D2=0101010110011001111000111101C3=0000110011001010101011111111D3=0101011001100111100011110101C4=0011001100101010101111111100D4=0101100110011110001111010101
🕞 3.2.5.3 置换选择2
56位输入按照置换表进行选择与重新排列,产生48位的输出
🕒 4. 高级加密标准(AES)
🕘 4.1 总体结构
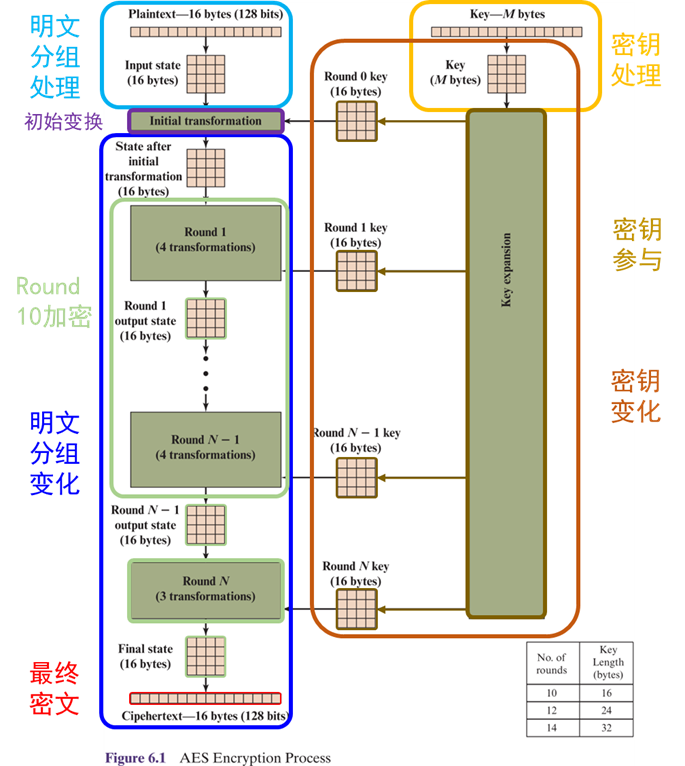
🕤 4.1.1 明文分组处理
-
AES明文分组128bit,每8bit构成一个字节,表示为十六进制
-
于是将AES的明文分组表示为16个字节的形式
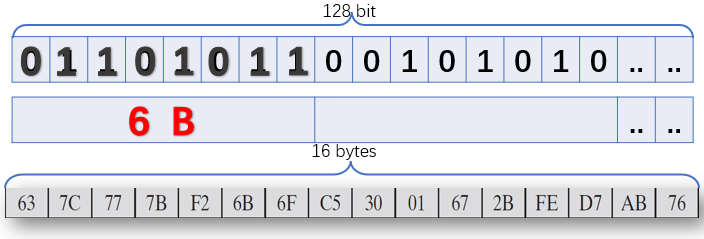
-
将16字节的明文分组按列填入4*4的矩阵
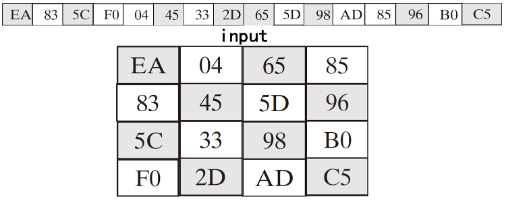
🕘 4.2 详细结构
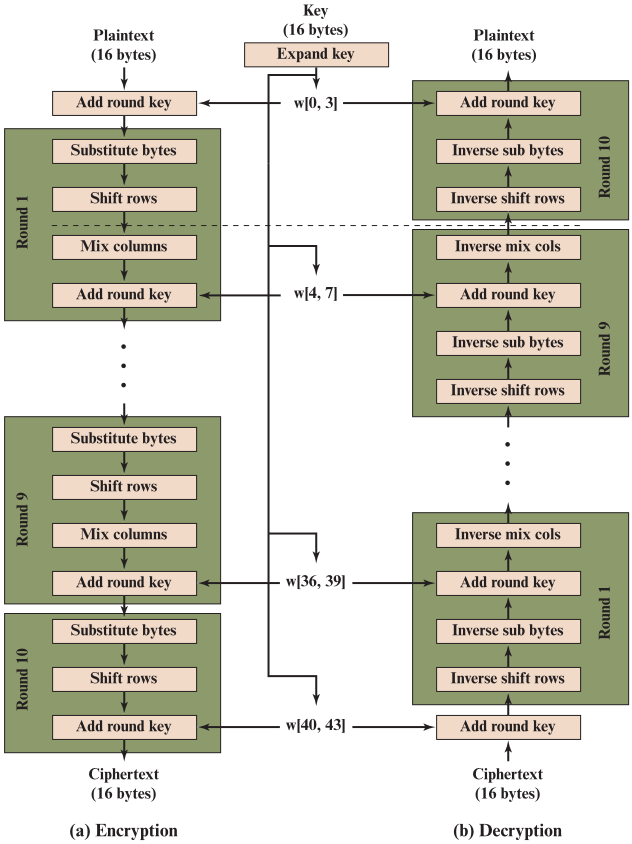
- AES 不是Feistel结构,没有用分组的一半去修改另一半然后交换
- 每一轮都使用代替和置换,将整个数据分组作为一个单一矩阵进行处理
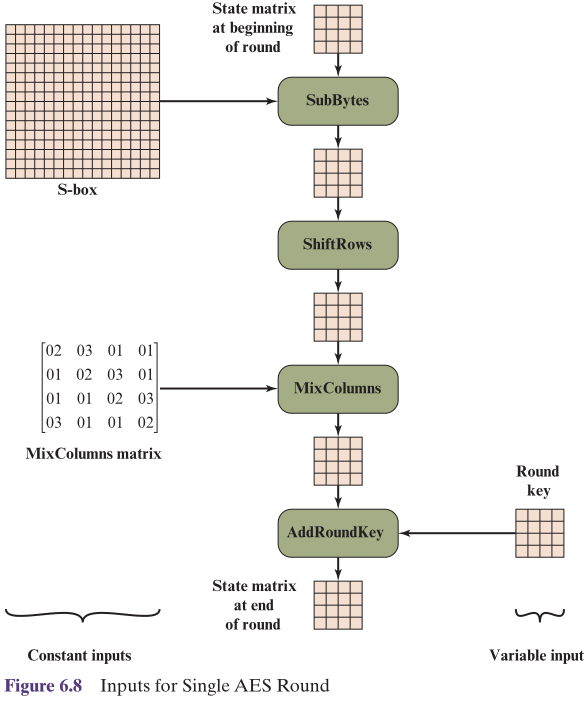
- 算法由初始变换“轮密钥加”开始,接着执行9轮加密运算,每轮都包含4个阶段
- 分别为字节代替(Substitute bytes)、行移位(ShiftRows)、列混淆(MixColumns)、轮密钥加(AddRoundKey)
🕤 4.2.1 AES的一轮加密

🕘 4.3 AES的变换函数
🕤 4.3.1 字节代替(Substitute bytes)
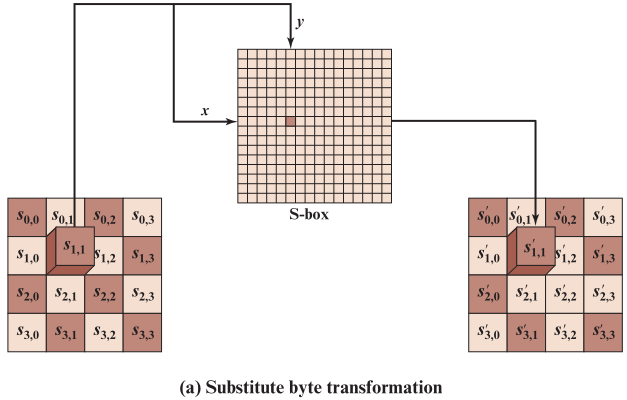
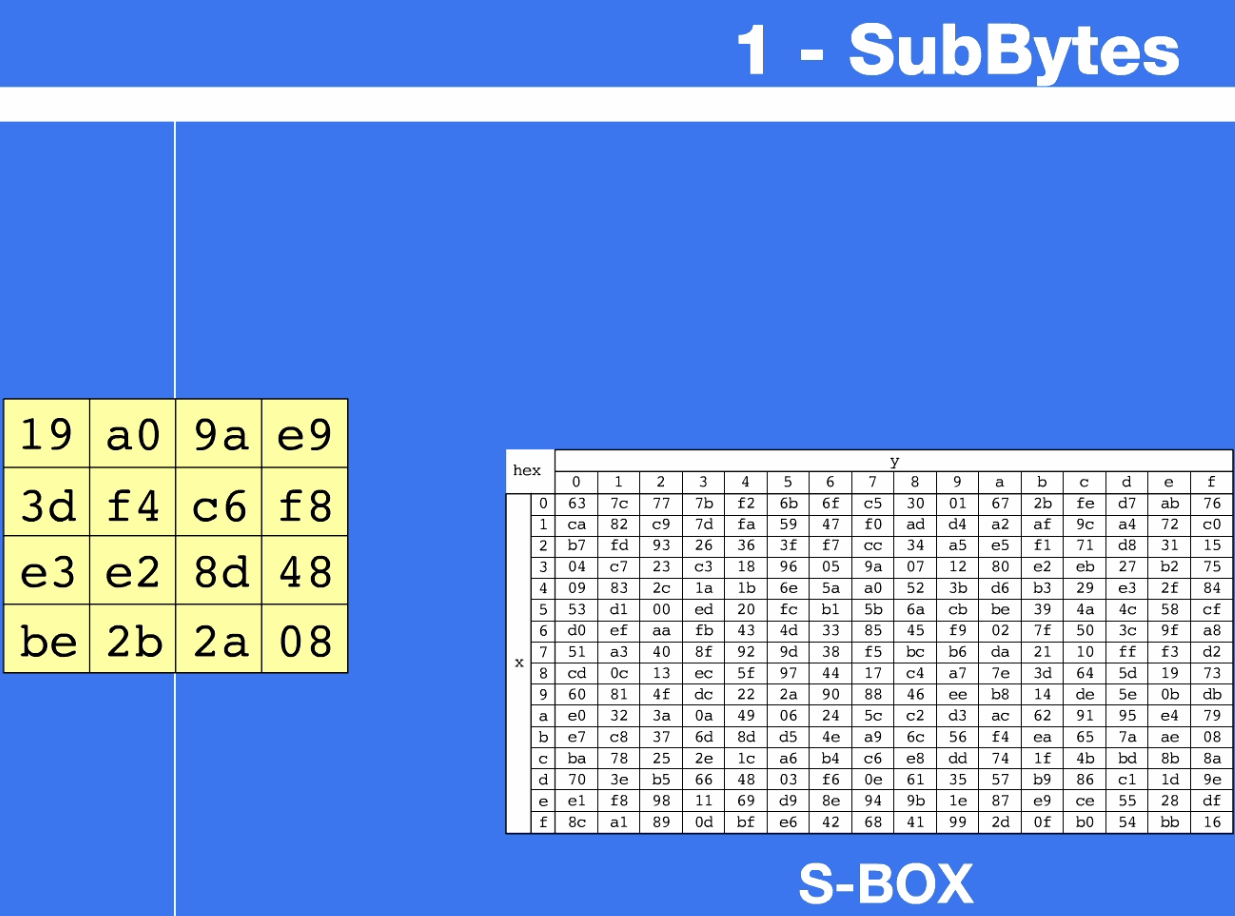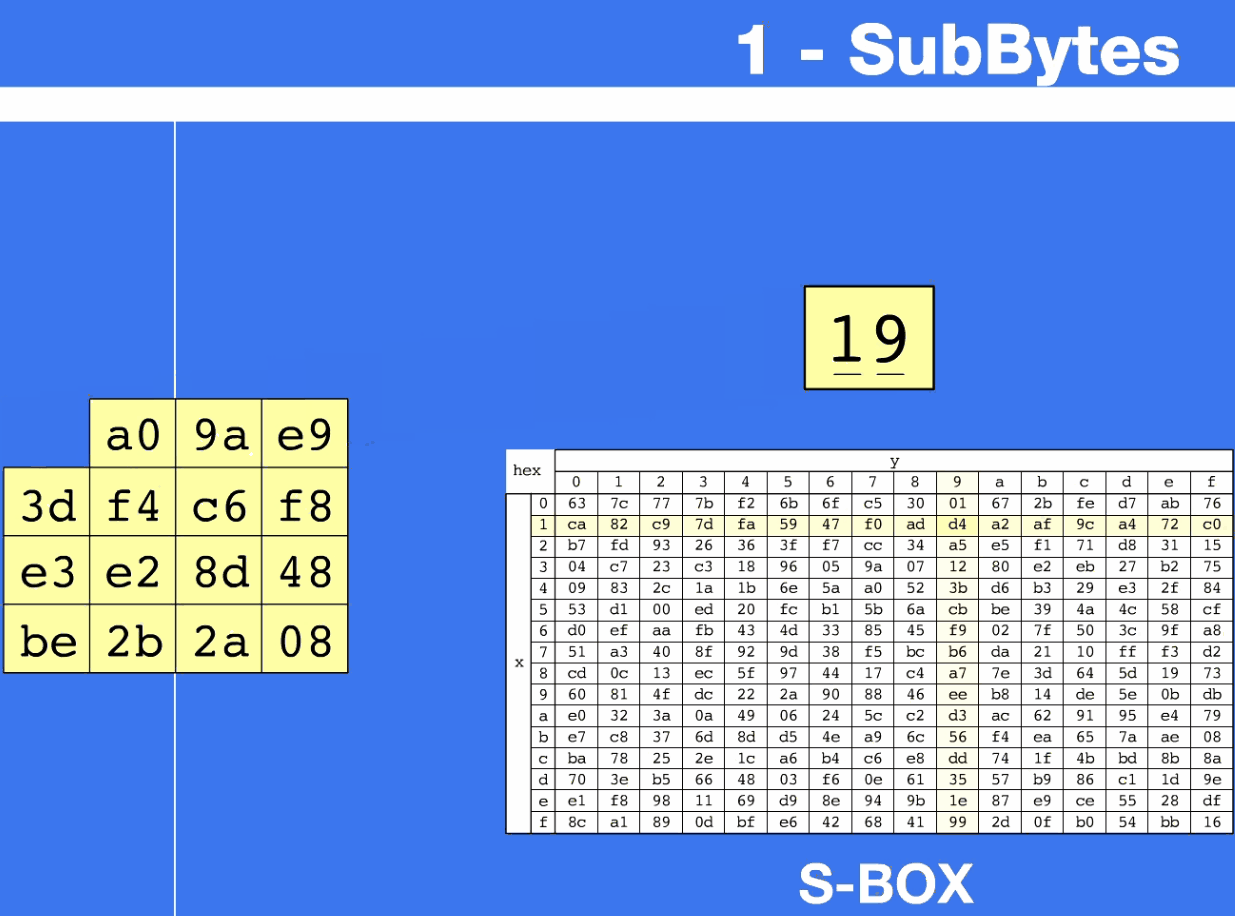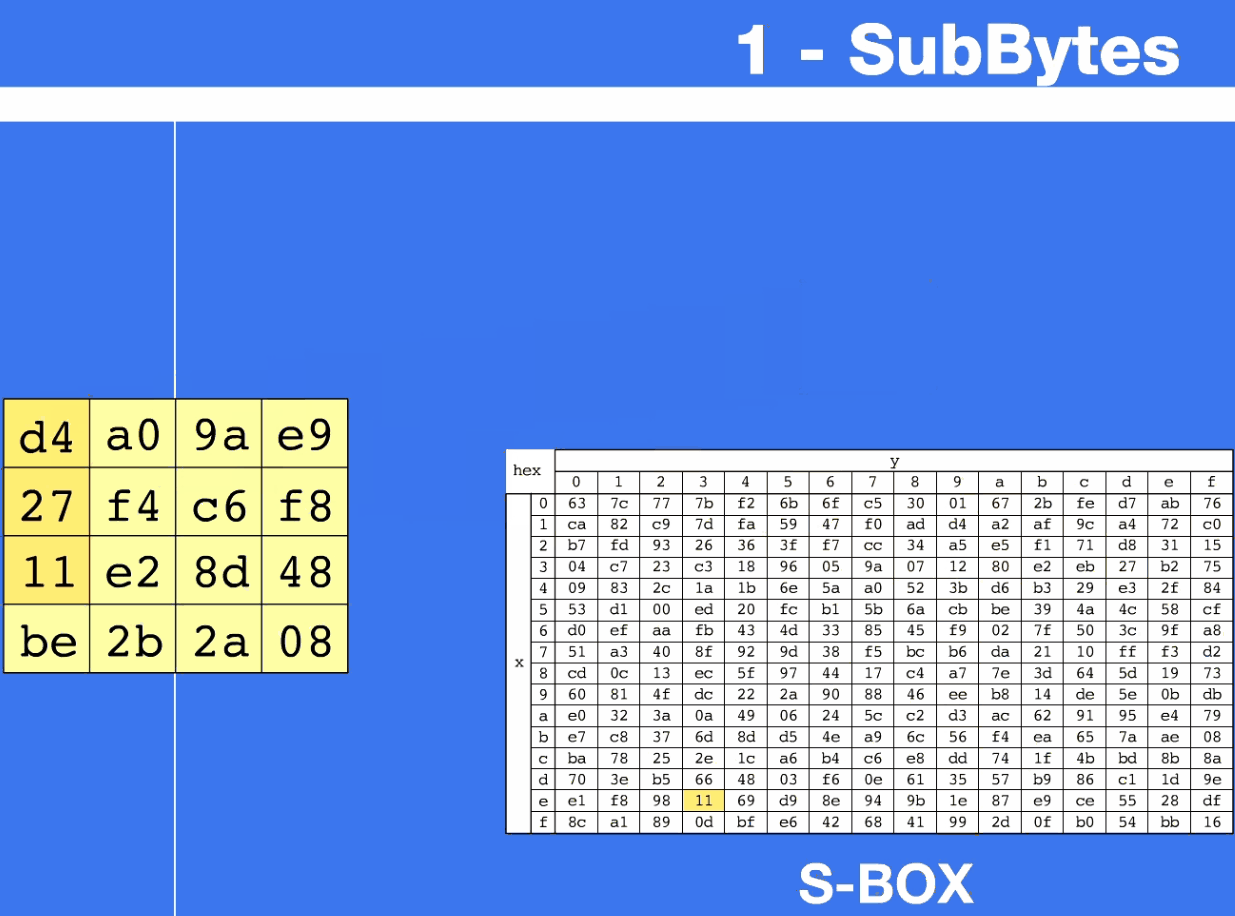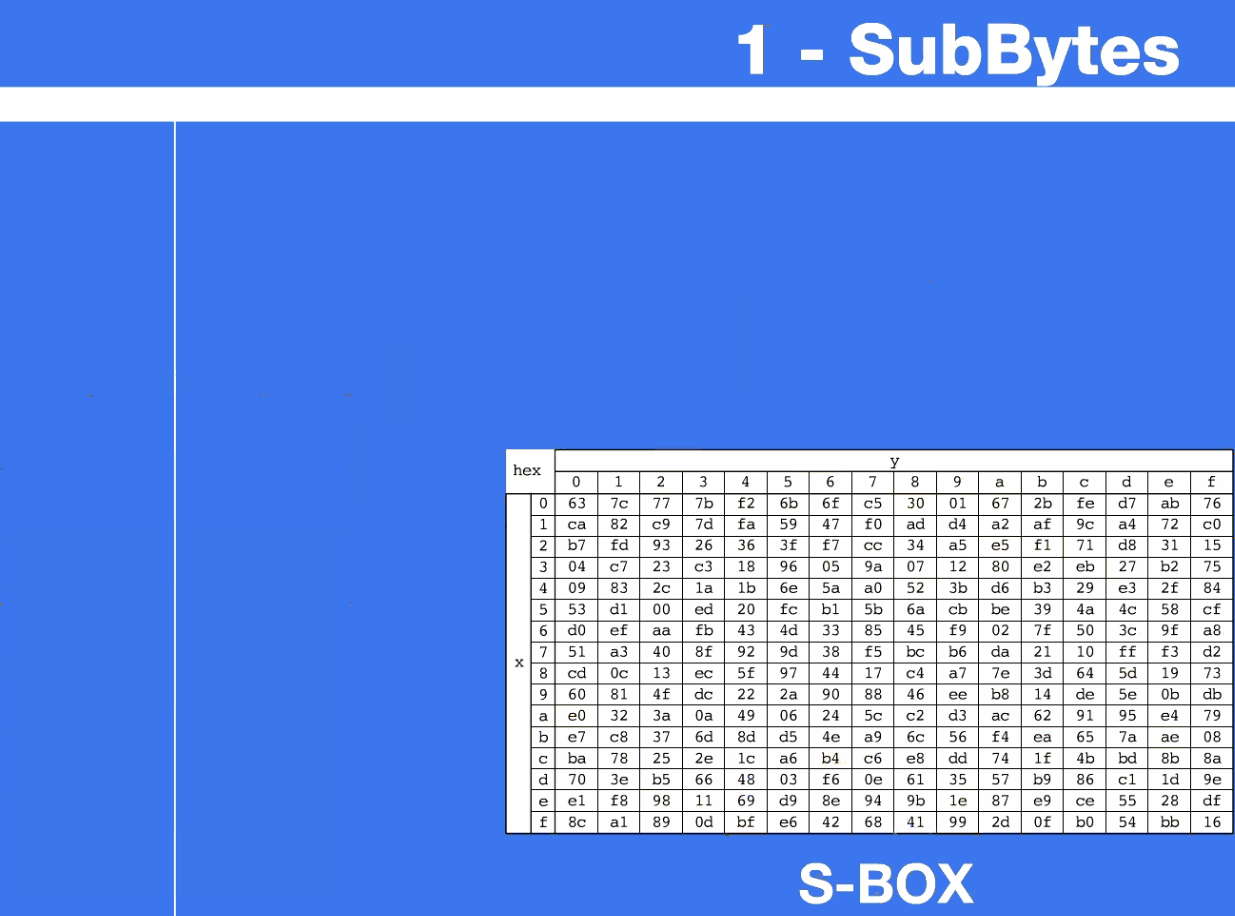
- AES 定义了一个S盒,由16*16个字节组成
- state的字节 𝑺 ( 𝟏 , 𝟏 ) = ( 𝒙 𝒚 ) 𝑺_{(𝟏,𝟏)}=(𝒙𝒚) S(1,1)=(xy),将𝒙作为行值,𝒚作为列值,S盒对应位置的元素就是新的 𝑺 ( 𝟏 , 𝟏 ) ′ 𝑺^′_{(𝟏,𝟏)} S(1,1)′
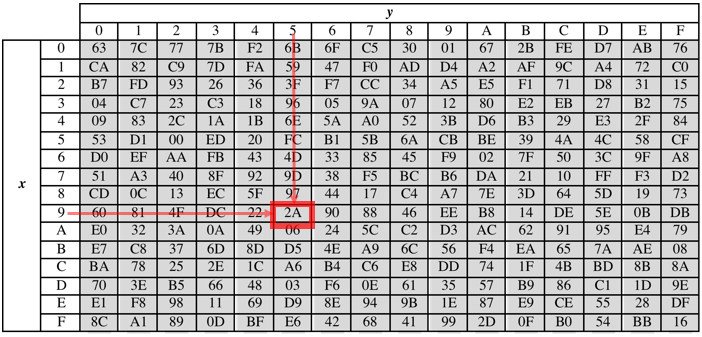
十六进制{95},行x=9,列y=5,经S盒被代替为{2A}
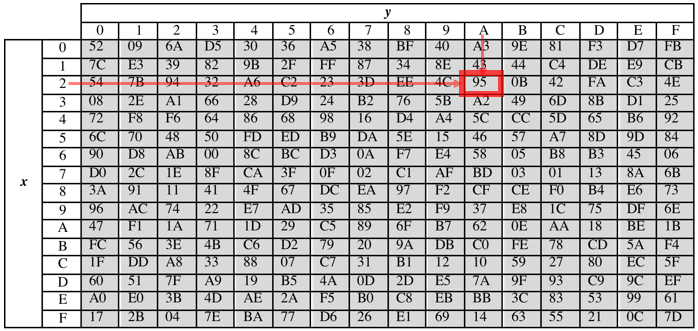
十六进制{2A},行x=2,列y=A,逆S盒将其代替为{95}
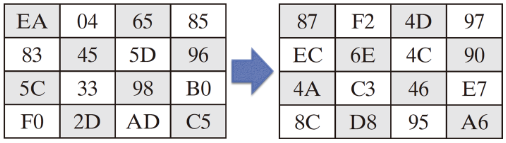
将当前state矩阵的各个字节依次输入S盒,字节代替结果如上所示
🕤 4.3.2 行移位(ShiftRows)
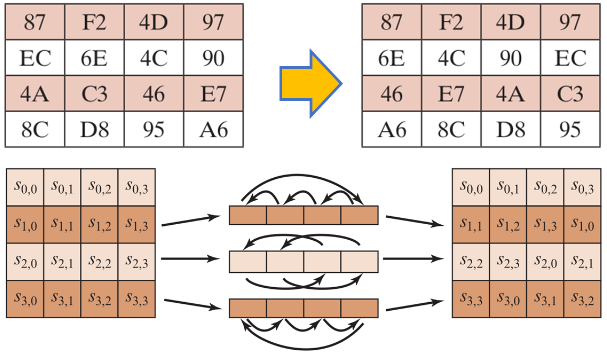

state矩阵的第一行保持不变,第二行循环左移1字节,第三行循环左移2字节,第四行左移3字节
🕤 4.3.3 列混淆(MixColumns)
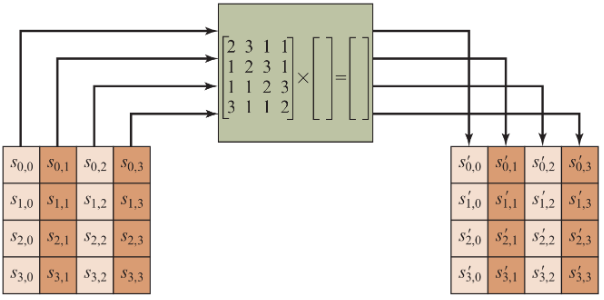

state矩阵的每一列左乘系数矩阵,相乘的结果作为新的列值
🕤 4.3.4 轮密钥加(AddRoundKey)
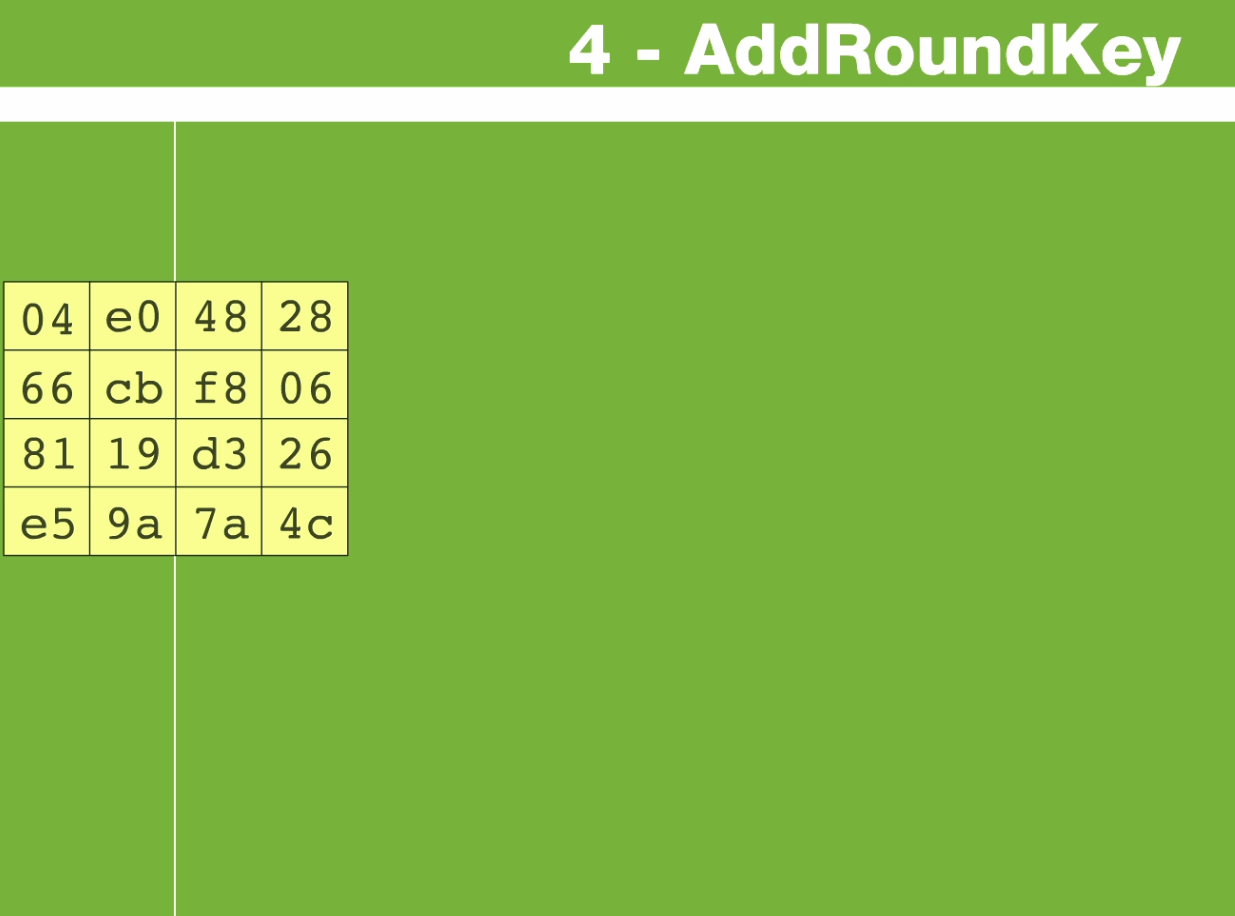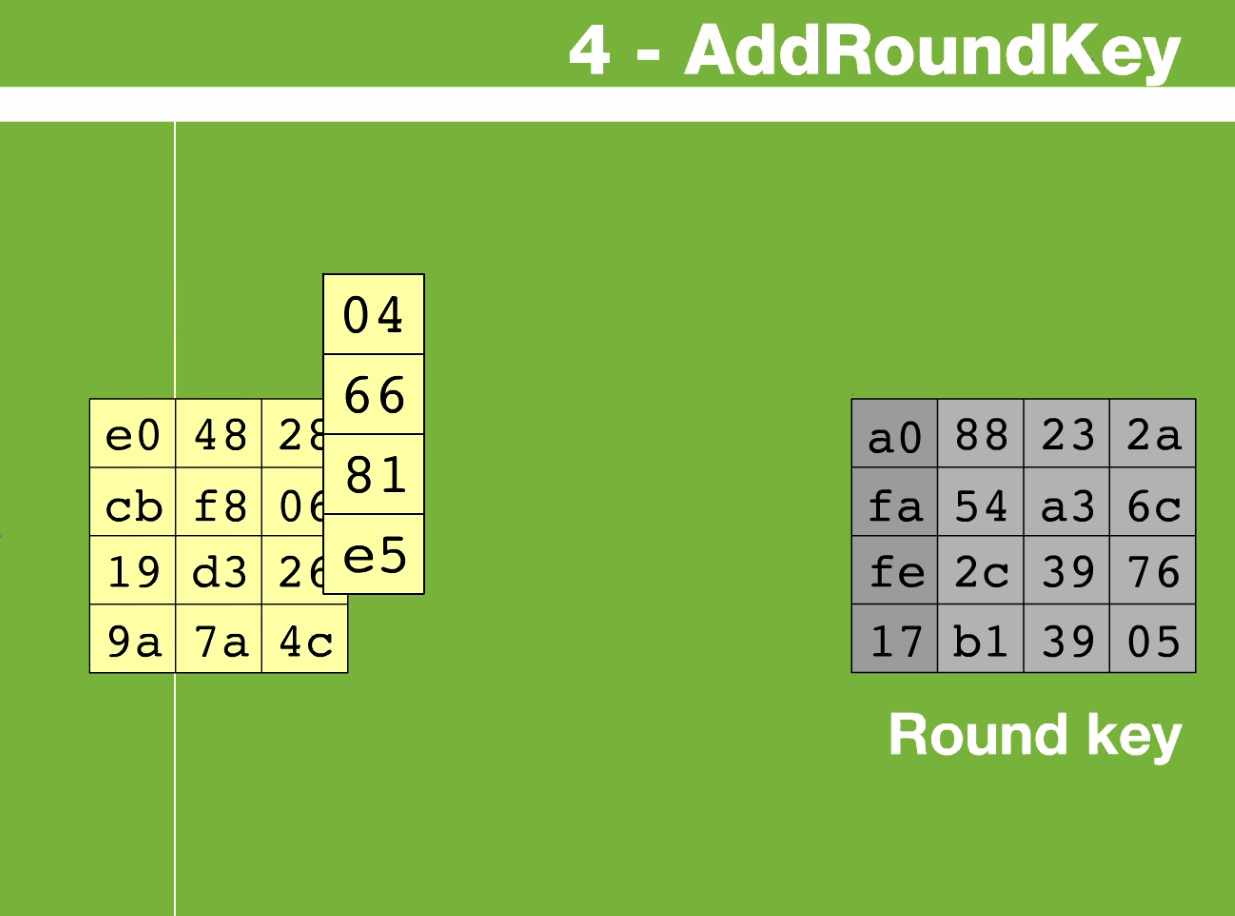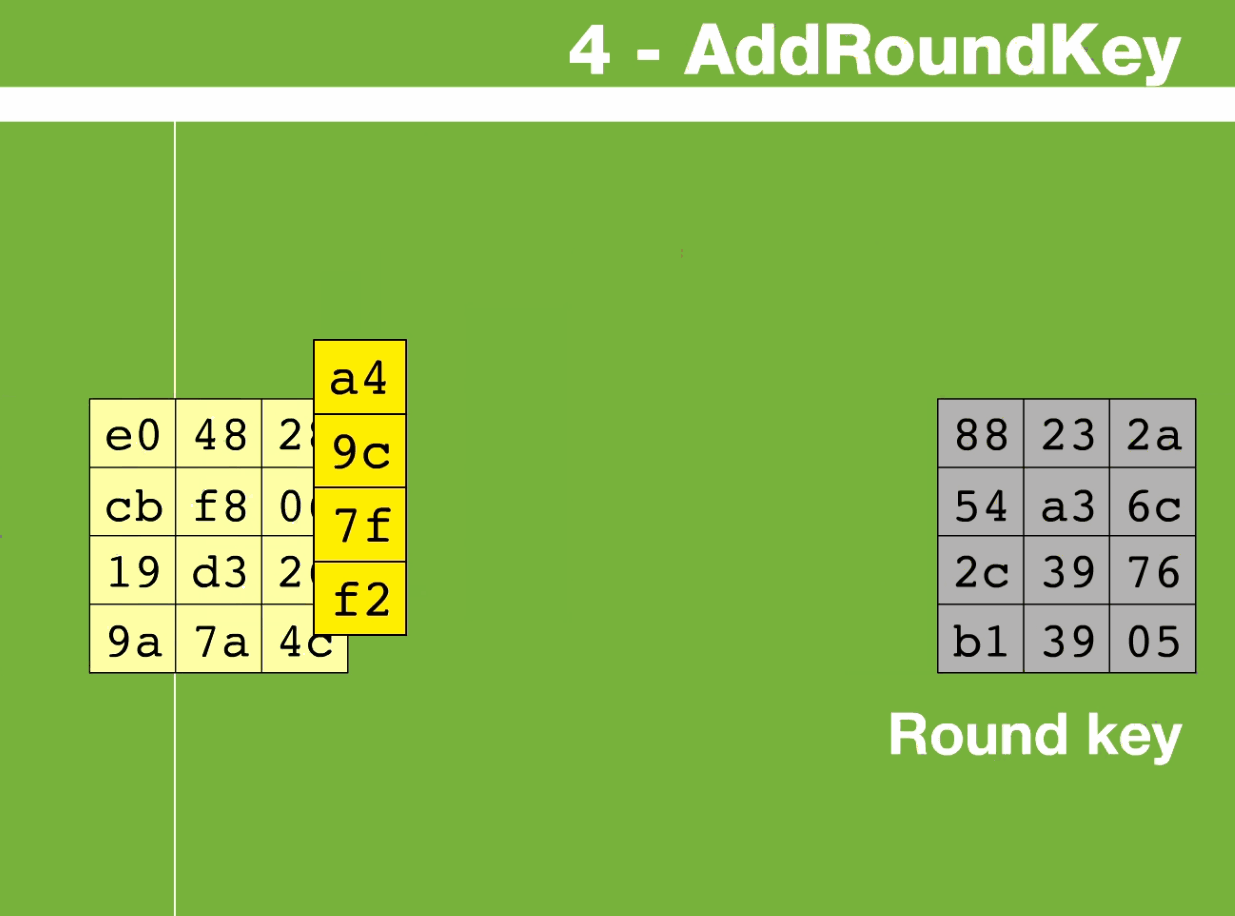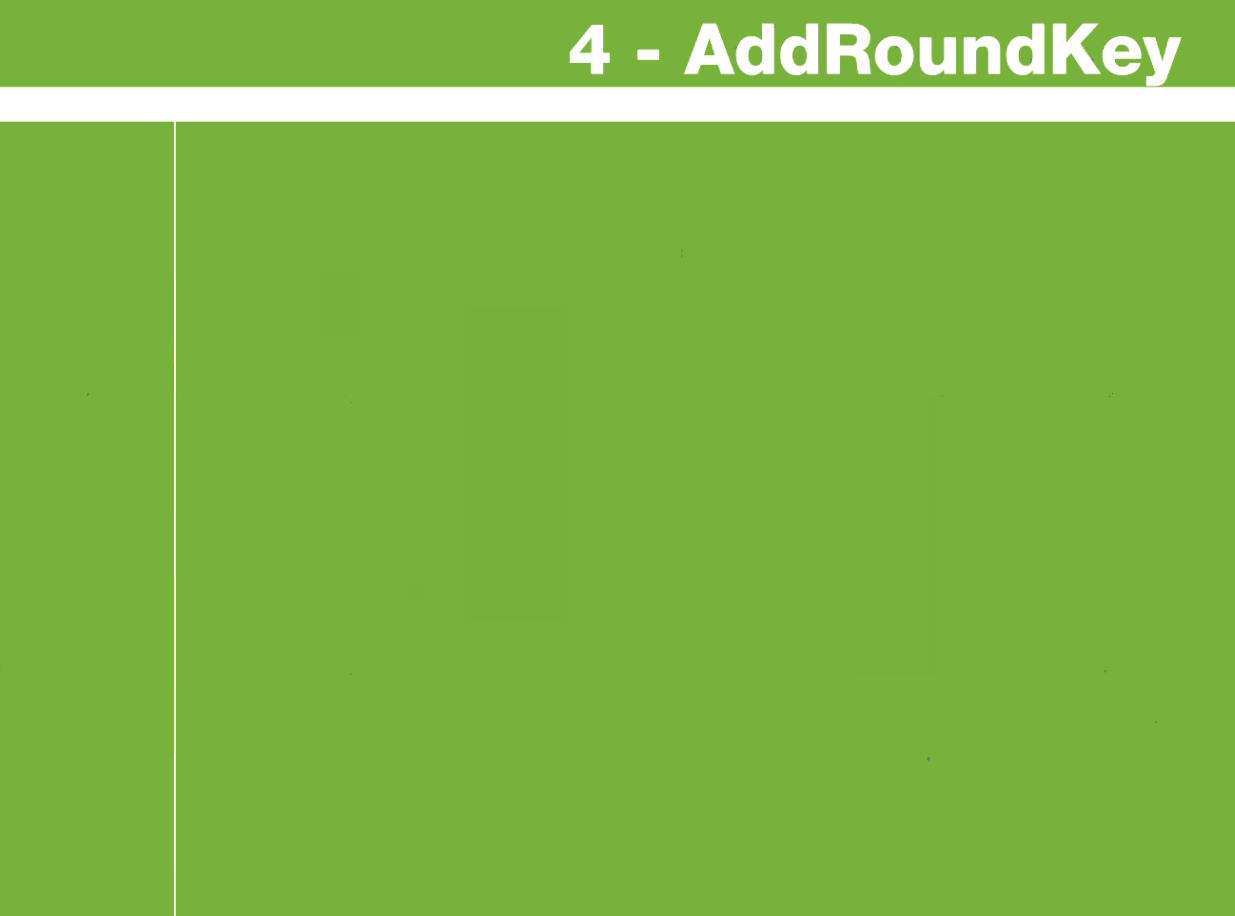
例中第一个矩阵是状态,第二个矩阵是轮密钥

将当前state矩阵与轮密钥矩阵的各个字节进行按位异或
如state中的{3A}与 轮密钥中的{29}进行XOR
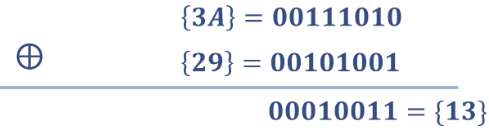
🕤 4.3.5 AES单轮输入

🕒 5. 分组加密的工作模式
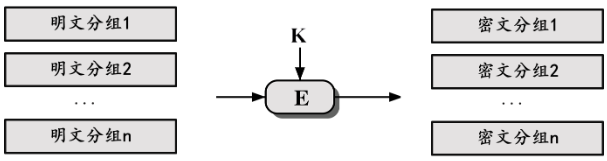
- 当明文长度b 超过了 分组长度n,需要将明文划分成一个个分组
- 而加密算法如何依次加密这些分组,就是工作模式
🕘 5.1 电码本ECB
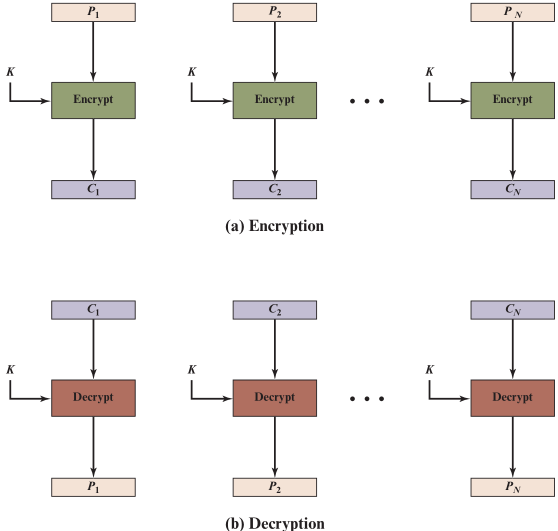
- 一次处理一个明文分组,每次使用相同的密钥加密
- 一段消息中若有几个明文分组,密文也将出现几个相同的密文分组
🕘 5.2 密文分组链接CBC
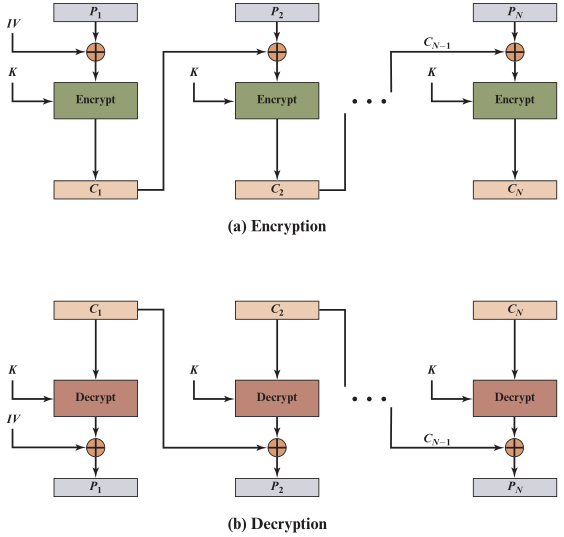
- 加密算法的输入是当前的明文分组 和 上一个密文分组的异或
- 重复的明文分组会被加密成不同的密文分组
🕘 5.3 密文反馈CFB
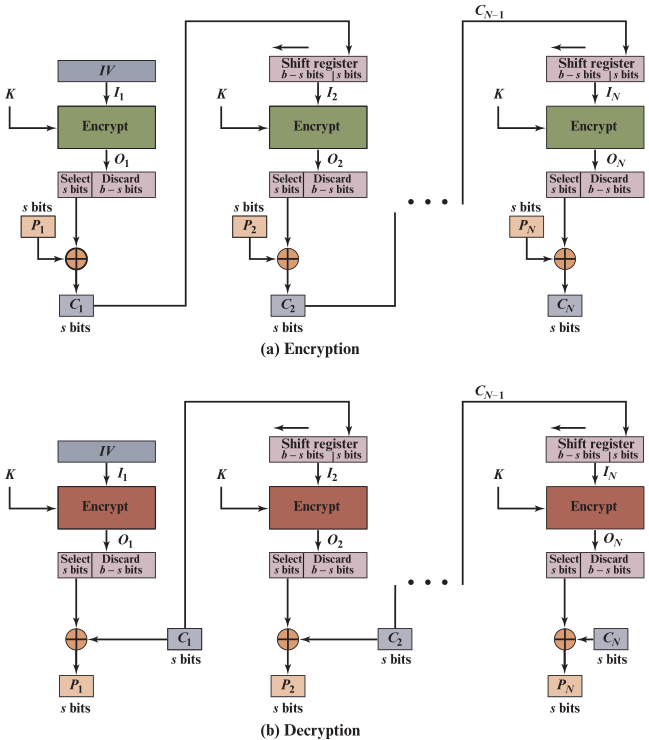
- 密文反馈模式CFB 对明文的处理类似于流密码
🕘 5.4 输出反馈OFB
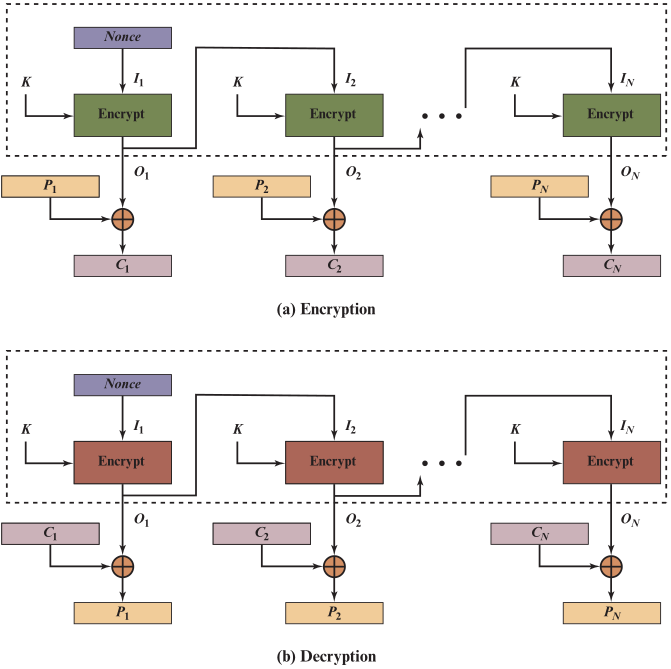
- 解密过程与CFB类似,也是将密文分组与一个特定的 𝑶 𝒊 𝑶_𝒊 Oi再次进行异或,还原出明文分组
无论是密文反馈模式CFB,还是输出反馈模式OFB,它们每一个分组的加密都要等待上一个加密流程的输出,所以无法并行地处理一段明文消息
🕘 5.5 计数器模式CTR
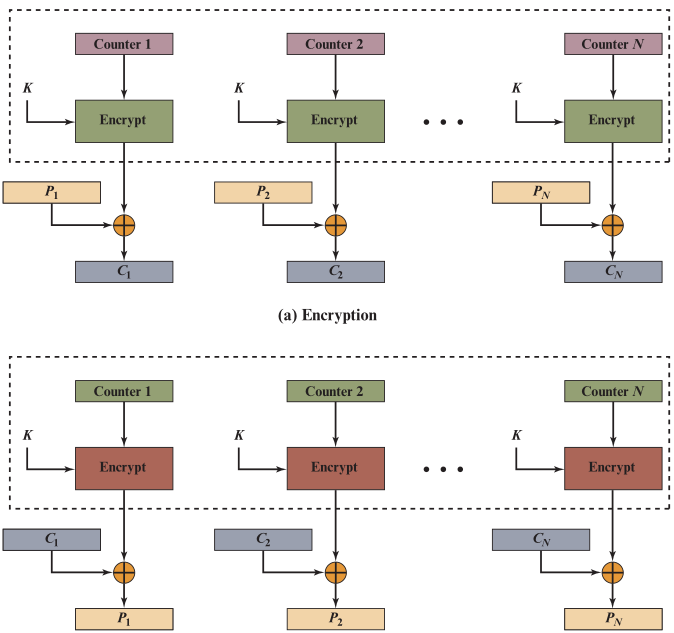
当确定了明文消息划分出的分组个数N后,就确定了N个计数器的值,加密后就确定了N个参与异或运算的输出值,可以并行地为明文分组进行异或。
| 模式 | 描述 | 典型应用 |
|---|---|---|
| Electronic Codebook (ECB) | 用相同的密钥分别对明文分组单独加密 | 单个数据的安全传输(如一个加密密钥) |
| Cipher Block Chaining (CBC) | 加密算法的输入是上一个密文分组和下一个明文分组的异或 | 面向分组的通用传输;认证 |
| Cipher Feedback (CFB) | 一次处理输入的s位,上一个密文分组作为加密算法的输入,产生的伪随机数输出与明文异或后作为下一个单元的密文 | 面向数据流的通用传输;认证 |
| Output Feedback (OFB) | 与CFB类似,只是加密算法的输入是上一次加密的输出,并且使用整个分组 | 噪声信道上的数据流的传输(如卫星通信) |
| Counter(CTR) | 每个明文分组都与一个经过加密的计数器异或。对每个后续的分组,计数器增1 | 面向分组的通用传输;用于高速需求 |
🕒 6. 公钥密码学与RSA
🕘 6.1 组成
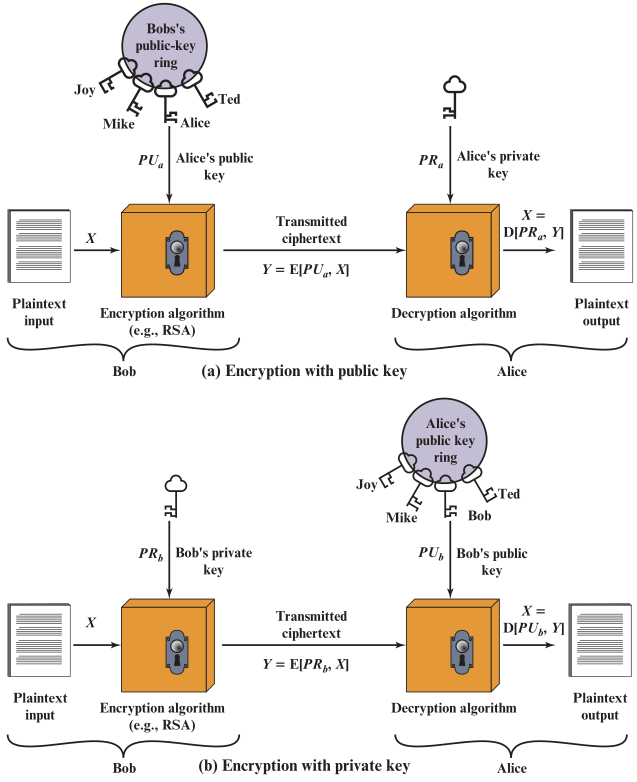
🕤 6.1.1 明文
通信双方发送的原始的、有意义的可读信息/数据,称为明文X
🕤 6.1.2 加密算法
加密算法E 将 明文X 进行各种转换
🕤 6.1.3 公钥
每个用户都产生一对密钥
其中一个是公开的,存放于公开寄存器或其他可访问的文件中,即公钥PU
🕤 6.1.4 私钥
每个用户都产生一对密钥
另外一个是私有的,只有自己才知道,即私钥PR
每个用户都有公钥PU、私钥PR
选用其中一把来加密,就用剩下的一把来解密
🕤 6.1.5 密文
加密算法E 读取 明文X 和 密钥PU/PR ,产生的输出就是 密文Y
🕤 6.1.6 解密算法
解密算法D 读取 密文Y 和 密钥PR/PU ,产生的输出就是 明文X
🕘 6.2 公钥加密
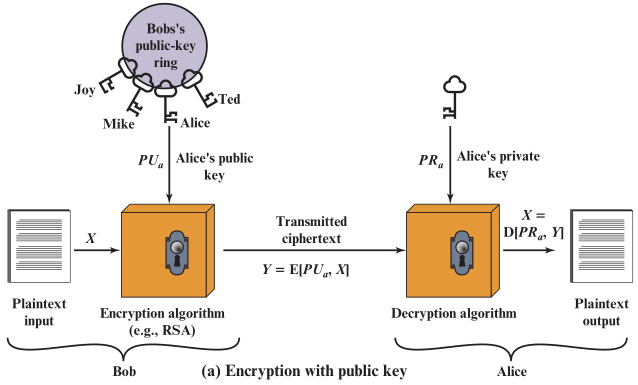
-
Bob 有一个公钥环,上面有很多人的公钥,当他要和某人进行通信,就选择对应的公钥来加密
-
Bob 现在要发送消息给Alice,所以选择Alice的公钥 𝑷 𝑼 𝒂 𝑷𝑼_𝒂 PUa, 将其加入到加密算法 E E E中
-
加密算法 E E E读取明文 X X X、公钥 𝑷 𝑼 𝒂 𝑷𝑼_𝒂 PUa,生成密文 Y Y Y
𝒀 = 𝑬 ( 𝑷 𝑼 𝒂 , 𝑿 ) 𝒀=𝑬(𝑷𝑼_𝒂,𝑿) Y=E(PUa,X) -
Alice收到了Bob发来的密文,使用自己的私钥 𝑷 𝑹 𝒂 𝑷𝑹_𝒂 PRa 来还原出明文
-
解密算法 D D D 读取密文 Y Y Y、私钥 𝑷 𝑹 𝒂 𝑷𝑹_𝒂 PRa,还原明文 X X X
𝑿 = 𝑫 ( 𝑷 𝑹 𝒂 , 𝒀 ) 𝑿=𝑫(𝑷𝑹_𝒂,𝒀) X=D(PRa,Y) -
由于解密使用的私钥只有 Alice自己知道,所以其他人无法解密 ,只有 Alice具有消息的访问权
🕘 6.3 私钥加密
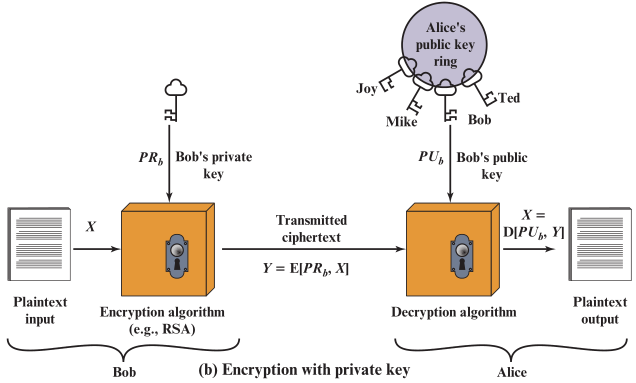
-
Bob 给Alice 发送明文 X X X,加密时使用的是他自己的私钥 𝑷 𝑹 𝒃 𝑷𝑹_𝒃 PRb,生成的密文为 Y Y Y
-
加密算法 E E E 读取明文 X X X 和私钥 𝑷 𝑹 𝒃 𝑷𝑹_𝒃 PRb,生成密文 Y Y Y
𝒀 = 𝑬 ( 𝑷 𝑹 𝒃 , 𝑿 ) 𝒀=𝑬(𝑷𝑹_𝒃,𝑿) Y=E(PRb,X) -
Alice 收到了Bob 发来的密文 Y Y Y,将其输入解密算法 D D D,并从公钥环中找出发送方Bob 的公钥 𝑷 𝑼 𝒃 𝑷𝑼_𝒃 PUb,还原出明文 X X X
-
解密算法 D D D 读取密文 Y Y Y 和公钥 𝑷 𝑼 𝒃 𝑷𝑼_𝒃 PUb,生成明文 X X X
𝑿 = 𝑫 ( 𝑷 𝑼 𝒃 , 𝒀 ) 𝑿=𝑫(𝑷𝑼_𝒃,𝒀) X=D(PUb,Y) -
𝒀 = 𝑬 ( 𝑷 𝑹 𝒃 , 𝑿 ) , 𝑿 = 𝑫 ( 𝑷 𝑼 𝒃 , 𝒀 ) 𝒀=𝑬(𝑷𝑹_𝒃,𝑿),𝑿=𝑫(𝑷𝑼_𝒃,𝒀) Y=E(PRb,X),X=D(PUb,Y)
-
Alice 收到了据说是Bob 发出的密文,若Alice 能使用Bob的公钥解密出明文,那么消息来源正确,因为只有Bob 才知道加密使用的私钥
🕘 6.4 双重加密
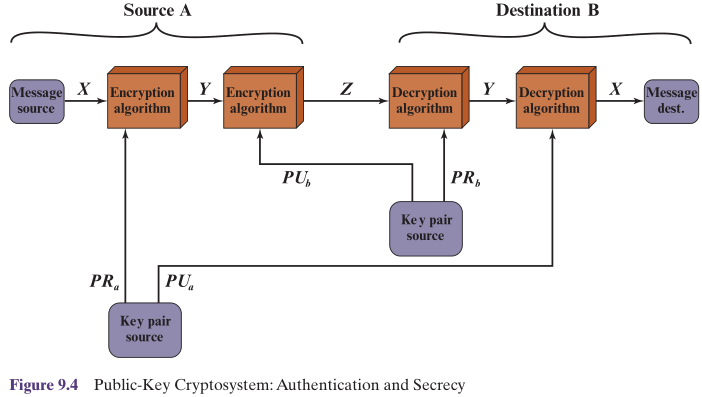
用发送方的私钥签名,用接收方的公钥加密
🕘 6.5 RSA算法☆☆☆
RSA是分组密码,用到的数学基础是:欧拉定理、大整数因子分解的困难性
- 挑选p、q
p = 17 , q = 11 p=17,q=11 p=17,q=11
- Alice 现在要产生自己的公钥PU 与 私钥PR
- 首先选择两个素数p、q,它们只能被1和自身整除,Alice选择了p=17,q=11
- p、q保密,Alice选定得到
- 计算n
𝒏 = 𝒑 𝒒 = 𝟏 𝟕 × 𝟏 𝟏 = 𝟏 𝟖 𝟕 𝒏=𝒑𝒒=𝟏𝟕×𝟏𝟏=𝟏𝟖𝟕 n=pq=17×11=187
- 然后计算这两个素数pq的乘积n=187
- n 公开,Alice计算得到
-
计算 ϕ ( 𝒏 ) \phi(𝒏) ϕ(n)
ϕ ( 𝒏 ) = ϕ ( 𝒑 𝒒 ) \phi(𝒏) = \phi(𝒑𝒒) ϕ(n)=ϕ(pq)
= ( 𝒑 − 𝟏 ) × ( 𝒒 − 𝟏 ) =(𝒑−𝟏)×(𝒒−𝟏) =(p−1)×(q−1)
= 𝟏 𝟔 × 𝟏 𝟎 = 𝟏 𝟔 𝟎 =𝟏𝟔×𝟏𝟎=𝟏𝟔𝟎 =16×10=160
计算乘积n的欧拉函数 ϕ ( 𝒏 ) = 160 \phi(𝒏)=160 ϕ(n)=160 -
挑选e
𝒈 𝒄 𝒅 ( ϕ ( 𝒏 ) , 𝒆 ) = 𝟏 𝒈𝒄𝒅(\phi(𝒏),𝒆)=𝟏 gcd(ϕ(n),e)=1 𝟏 < 𝒆 < ϕ ( 𝒏 ) 𝟏<𝒆< \phi(𝒏) 1<e<ϕ(n)
- 选出一个e,使得e与 ϕ ( 𝒏 ) \phi(𝒏) ϕ(n)互素,且保证e小于 ϕ ( 𝒏 ) \phi(𝒏) ϕ(n),Alice挑选的 e = 7 e=7 e=7
- e 公开,Alice选定得到
- 计算d
𝒅 ≡ 𝒆 ( − 𝟏 ) ( 𝒎 𝒐 𝒅 ϕ ( 𝒏 ) ) 𝒅\equiv𝒆^{(−𝟏) } ( 𝒎𝒐𝒅 \phi(𝒏) ) d≡e(−1)(modϕ(n))
- 计算数值d,即求e在 m o d 160 mod 160 mod160下的乘法逆元,使用扩展欧几里得算法
- d 保密,由Alice计算得到
插播:扩展欧几里得算法
7
(
𝒎
𝒐
𝒅
160
)
7 \ (𝒎𝒐𝒅 160)
7 (mod160)
𝒈
𝒄
𝒅
(
160
,
7
)
=
𝟏
𝒈𝒄𝒅(160,7)=𝟏
gcd(160,7)=1
7
𝒚
(
𝒎
𝒐
𝒅
160
)
=
𝟏
7𝒚(𝒎𝒐𝒅 160)=𝟏
7y(mod160)=1
7
𝒚
=
160
𝒙
+
𝟏
7𝒚=160𝒙+𝟏
7y=160x+1
7
𝒚
−
160
𝒙
=
𝟏
7𝒚−160𝒙=𝟏
7y−160x=1
160
𝒙
+
7
𝒚
=
𝟏
=
𝒈
𝒄
𝒅
(
160
,
7
)
160𝒙+7𝒚=𝟏=𝒈𝒄𝒅(160,7)
160x+7y=1=gcd(160,7)
ϕ ( n ) e q i d x i y i 160 7 22 1 − 1 23 7 6 1 1 1 − 1 6 1 6 1 0 1 1 0 1 1 0 \begin{array}{|c|c|c|c|c|c|} \hline \phi(n) & e & q_{i} & \mathrm{~d} & x_{i} & y_{i} \\ \hline 160 & 7 & 22 & 1 & -1 & 23 \\ \hline 7 & 6 & 1 & 1 & 1 & -1 \\ \hline 6 & 1 & 6 & 1 & 0 & 1 \\ \hline 1 & 0 & & 1 & 1 & 0 \\ \hline \end{array} ϕ(n)160761e7610qi2216 d1111xi−1101yi23−110
因此x=23=d,即所求乘法逆元
- 组成公私钥
𝑷 𝑼 𝒂 = { 𝒆 , 𝒏 } = { 𝟕 , 𝟏 𝟖 𝟕 } 𝑷𝑼_𝒂=\{𝒆,𝒏\}=\{𝟕,𝟏𝟖𝟕\} PUa={e,n}={7,187}
𝑷 𝑹 𝒂 = { 𝒅 , 𝒏 } = { 𝟐 𝟑 , 𝟏 𝟖 𝟕 } 𝑷𝑹_𝒂=\{𝒅,𝒏\}=\{𝟐𝟑,𝟏𝟖𝟕\} PRa={d,n}={23,187}
- 将数值组合{e,n}作为公钥公开,将{d,n}作为私钥保密
- 生成密文Y
-
Bob 要给Alice 发送消息X,使用Alice的公钥 𝑷 𝑼 𝒂 𝑷𝑼_𝒂 PUa 加密
-
算法规定将公钥中的数值e作为幂值,将数值n作为模数
𝒀 = 𝑬 ( 𝑷 𝑼 𝒂 , 𝑿 ) 𝒀=𝑬(𝑷𝑼_𝒂,𝑿) Y=E(PUa,X)
= 𝑬 ( 𝒆 , 𝒏 , 𝑿 ) =𝑬({𝒆,𝒏},𝑿) =E(e,n,X)
= 𝑿 𝒆 𝒎 𝒐 𝒅 𝒏 =𝑿^𝒆 \ 𝒎𝒐𝒅 \ 𝒏 =Xe mod n
= 𝟖 𝟖 𝟕 𝒎 𝒐 𝒅 𝟏 𝟖 𝟕 =𝟖𝟖^𝟕 \ 𝒎𝒐𝒅 \ 𝟏𝟖𝟕 =887 mod 187 -
RSA 也是分组密码,可以处理的明文X < n
-
若Bob发送的明文X=88,Alice的公钥为{7,187},得出密文Y=11
- 还原明文X
-
Alice 收到密文Y后,使用她自己的私钥 𝑷 𝑹 𝒂 𝑷𝑹_𝒂 PRa进行解密
-
解密算法函数与加密相同,仍然将密钥第一部分d作为幂值,第二部分n作为模数
𝑿 = 𝑫 ( 𝑷 𝑹 𝒂 , 𝒀 ) 𝑿=𝑫(𝑷𝑹_𝒂,𝒀) X=D(PRa,Y)
= 𝑫 ( { 𝒅 , 𝒏 } , 𝒀 ) =𝑫(\{𝒅,𝒏\},𝒀) =D({d,n},Y)
= 𝒀 𝒅 𝒎 𝒐 𝒅 𝒏 =𝒀^𝒅 \ 𝒎𝒐𝒅 \ 𝒏 =Yd mod n
= 𝟏 𝟏 𝟐 𝟑 𝒎 𝒐 𝒅 𝟏 𝟖 𝟕 =𝟏𝟏^{𝟐𝟑} \ 𝒎𝒐𝒅 \ 𝟏𝟖𝟕 =1123 mod 187 -
私钥 𝑷 𝑹 𝒂 = { 23 , 187 } 𝑷𝑹_𝒂=\{23,187\} PRa={23,187}
-
计算得到的结果X=88,与Bob发送的原始数值相同
小结:
- 素数 p , q p, q p,q
- n = p × q \boldsymbol{n}=\boldsymbol{p} \times \boldsymbol{q} n=p×q
- ϕ ( n ) = ( p − 1 ) × ( q − 1 ) \boldsymbol{\phi}(\boldsymbol{n})=(\boldsymbol{p}-\mathbf{1}) \times(\boldsymbol{q}-\mathbf{1}) ϕ(n)=(p−1)×(q−1)
- gcd ( e , ϕ ( n ) ) = 1 \operatorname{gcd}(e, \phi(n))=1 gcd(e,ϕ(n))=1
- d ≡ e − 1 ( m o d ϕ ( n ) ) d \equiv e^{-1}(\bmod \phi(n)) d≡e−1(modϕ(n))
- P U = { e , n } , P R = { d , n } P U=\{e, n\}, P R=\{d, n\} PU={e,n},PR={d,n}
- Y = X e m o d n Y=X^{e} \bmod n Y=Xemodn
- X = Y d m o d n X =Y^{d} \bmod n X=Ydmodn
练习题:
已知p=17,q=2,请使用RSA算法计算出一对公钥与私钥,并使用公钥加密明文消息“3”。
解答:已知 p=17, q=2
n = p × q = 17 × 2 = 34 n=p\times q=17\times 2=34 n=p×q=17×2=34
ϕ ( n ) = ( p − 1 ) ( q − 1 ) = 16 × 1 = 16 \phi(n)=(p-1)(q-1)=16\times 1=16 ϕ(n)=(p−1)(q−1)=16×1=16
选取 e e e使其与 ϕ ( n ) \phi(n) ϕ(n)互素,令 e = 3 e=3 e=3
计算 d d d,使得 d × e = 1 ( m o d ϕ ( n ) ) d\times e =1 (mod \ \phi (n)) d×e=1(mod ϕ(n)),即 d = e − 1 m o d 16 = 3 − 1 m o d 16 d=e^{-1} \ mod \ 16 = 3^{-1} \ mod \ 16 d=e−1 mod 16=3−1 mod 16
根据扩展欧几里得算法,有 3 x + 16 y = g c d ( 3 , 16 ) 3x+16y=gcd(3,16) 3x+16y=gcd(3,16)
ϕ ( n ) e q i d x i y i 16 3 5 1 1 − 5 3 1 3 1 0 1 1 0 1 1 0 \begin{array}{|c|c|c|c|c|c|} \hline \phi(n) & e & q_{i} & \mathrm{~d} & x_{i} & y_{i} \\ \hline 16 & 3 & 5 & 1 & 1 & -5 \\ \hline 3 & 1 & 3 & 1 & 0 & 1 \\ \hline 1 & 0 & & 1 & 1 & 0 \\ \hline \end{array} ϕ(n)1631e310qi53 d111xi101yi−510
得 x = − 5 ( m o d 16 ) = 11 x = -5 (mod 16)= 11 x=−5(mod16)=11即 d = 11 d = 11 d=11
因此公钥 { e , n } = { 3 , 34 } \{e, n\}=\{3,34\} {e,n}={3,34},私钥 { d , n } = { 11 , 34 } \{d, n\}=\{11,34\} {d,n}={11,34}。
密文 C = x e m o d n = 3 3 m o d 34 = 27 C=x^e \ mod \ n = 3^3 \ mod \ 34 = 27 C=xe mod n=33 mod 34=27。
🕒 7. 密钥管理和其他公钥体制
🕘 7.1 Diffie-Hellman 密钥交换
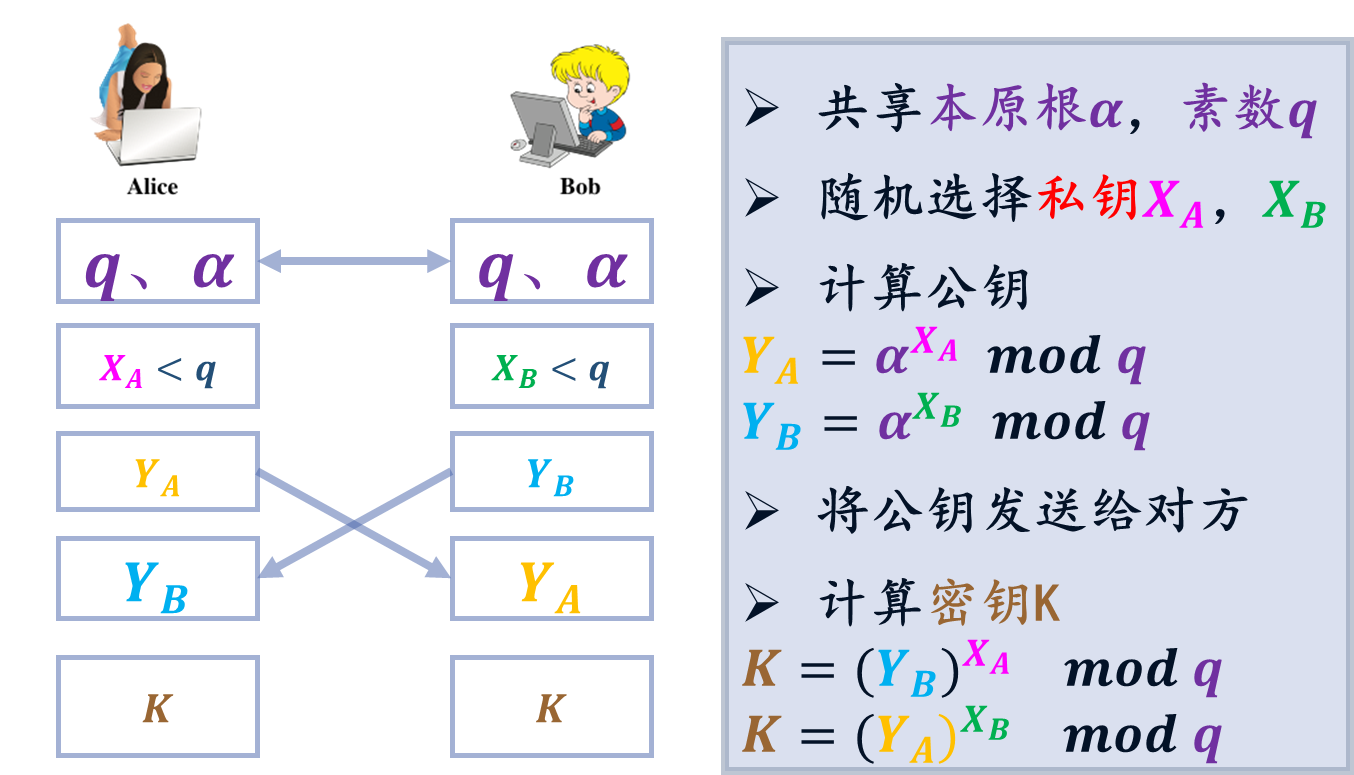
- Alice和Bob要进行密钥交换,首先他们共享一个素数 q q q以及整数𝜶,并公开
- 𝜶<𝒒,𝜶是素数q的本原根
- Alice 选择随机整数 𝑿 𝑨 < 𝒒 , 𝑿 𝑨 𝑿_𝑨<𝒒,𝑿_𝑨 XA<q,XA是私有的,只有Alice自己知道,即Alice的私钥
- Bob 也选择一个随机整数 𝑿 𝑩 < 𝒒 𝑿_𝑩<𝒒 XB<q,作为Bob 的私钥
- Alice 计算 𝒀 𝑨 = a 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 𝒀_𝑨=a^{𝑿_𝑨} \ 𝒎𝒐𝒅 \ 𝒒 YA=aXA mod q,计算得到的 𝒀 𝑨 𝒀_𝑨 YA是公开可访问的,即Alice的公钥
- Bob 也计算他的公钥 𝒀 𝑩 = a 𝑿 𝑩 𝒎 𝒐 𝒅 𝒒 𝒀_𝑩=a^{𝑿_𝑩} \ 𝒎𝒐𝒅 \ 𝒒 YB=aXB mod q
- Alice 将自己的公钥 𝒀 𝑨 𝒀_𝑨 YA发送给 Bob,Bob获取到了Alice 的公钥
- Bob 也将他的公钥 𝒀 𝑩 𝒀_𝑩 YB发送给了Alice
- Alice 计算 𝑲 = ( 𝒀 𝑩 ) 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 𝑲=(𝒀_𝑩)^{𝑿_𝑨} \ 𝒎𝒐𝒅 \ 𝒒 K=(YB)XA mod q
- Bob 也使用该方法计算 𝑲 = ( 𝒀 𝑨 ) 𝑿 𝑩 𝒎 𝒐 𝒅 𝒒 𝑲=(𝒀_𝑨)^{𝑿_𝑩} \ 𝒎𝒐𝒅 \ 𝒒 K=(YA)XB mod q
- 二人计算结果相同,至此双方完成了 K K K的交换
- K K K值在双方本地生成,且只有双方已知,因此常将这个 K K K值作为对称密码的密钥
证明: 𝑲 = ( 𝒀 𝑩 ) 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 𝑲=(𝒀_𝑩)^{𝑿_𝑨} \ 𝒎𝒐𝒅 \ 𝒒 K=(YB)XA mod q
= ( a 𝑿 𝑩 𝒎 𝒐 𝒅 𝒒 ) 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 (a^{𝑿_𝑩 } \ 𝒎𝒐𝒅 \ 𝒒 )^{𝑿_𝑨} \ 𝒎𝒐𝒅 \ 𝒒 (aXB mod q)XA mod q
= ( a 𝑿 𝑩 ) 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 (a^{𝑿_𝑩 })^{𝑿_𝑨} \ 𝒎𝒐𝒅 \ 𝒒 (aXB)XA mod q
= a 𝑿 𝑩 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 a^{𝑿_𝑩 𝑿_𝑨 } \ 𝒎𝒐𝒅 \ 𝒒 aXBXA mod q
= ( a 𝑿 𝑨 ) 𝑿 𝑩 𝒎 𝒐 𝒅 𝒒 (a^{𝑿_𝑨 })^{𝑿_𝑩} \ 𝒎𝒐𝒅 \ 𝒒 (aXA)XB mod q
= ( a 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 ) 𝑿 𝑩 𝒎 𝒐 𝒅 𝒒 (a^{𝑿_𝑨 } \ 𝒎𝒐𝒅 \ 𝒒)^{𝑿_𝑩} \ 𝒎𝒐𝒅 \ 𝒒 (aXA mod q)XB mod q
= ( 𝒀 𝑨 ) 𝑿 𝑩 𝒎 𝒐 𝒅 𝒒 {(𝒀_𝑨)}^{𝑿_𝑩 } \ 𝒎𝒐𝒅 \ 𝒒 (YA)XB mod q
练习题
已知A和B使用Diffie-Hellman密钥交换算法,共享参数q=11,它的一个本原根a=6,A的私钥为3,B的私钥为4,计算通信密钥K。
解答:已知 q = 11 q = 11 q=11, a = 6 a = 6 a=6, X A = 3 X_A= 3 XA=3, X B = 4 X_B= 4 XB=4,则:
A A A的公钥 Y A = a X A m o d q = 6 3 m o d 11 = 7 Y_A = a^{X_A} \ mod \ q = 6^3 \ mod \ 11 = 7 YA=aXA mod q=63 mod 11=7,
B B B的公钥 Y B = a A B m o d q = 6 4 m o d 11 = 9 Y_B = a^{A_B} \ mod \ q = 6^4 \ mod \ 11 = 9 YB=aAB mod q=64 mod 11=9,
通信密钥 K = Y B X A m o d q = 9 3 m o d 11 = 3 K = Y_B^{X_A} \ mod \ q = 9^3 \ mod \ 11 = 3 K=YBXA mod q=93 mod 11=3
或者 K = Y A X B m o d q = 7 4 m o d 11 = 3 K = Y_A^{X_B} \ mod \ q = 7^4 \ mod \ 11 = 3 K=YAXB mod q=74 mod 11=3。
🕘 7.2 EIGamal 密钥交换
-
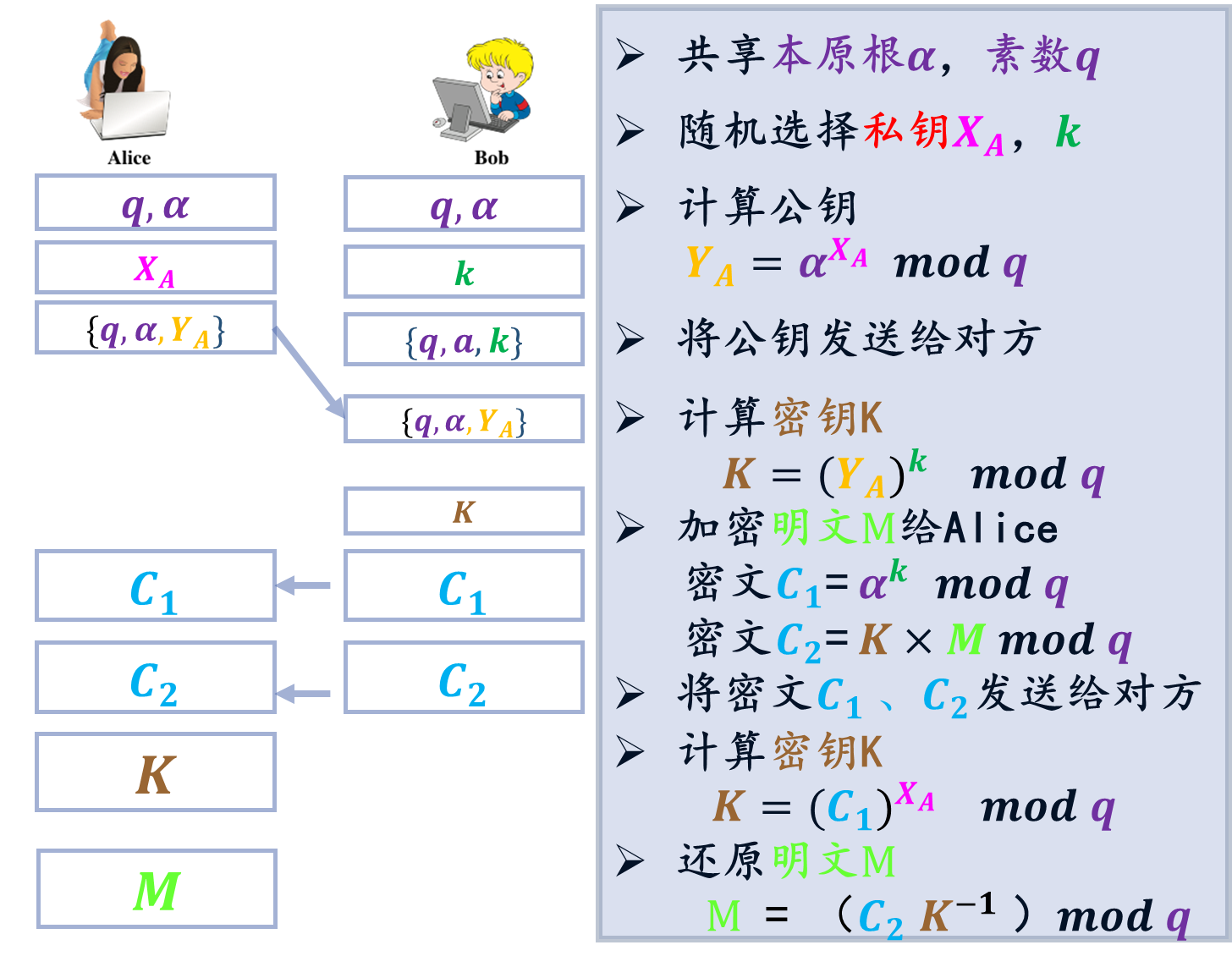
𝒒 = 𝟏 𝟗 , a = 𝟏 𝟎 𝒒=𝟏𝟗,a=𝟏𝟎 q=19,a=10
-
Alice 选择私钥 𝑿 𝑨 = 𝟓 𝑿_𝑨=𝟓 XA=5( X A < q − 1 X^A <q-1 XA<q−1),计算 𝒀 𝑨 = a 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 = 𝟏 𝟎 𝟓 𝒎 𝒐 𝒅 𝟏 𝟗 = 𝟑 𝒀_𝑨=a^{𝑿_𝑨} \ 𝒎𝒐𝒅 \ 𝒒 = 𝟏𝟎^𝟓 \ 𝒎𝒐𝒅 \ 𝟏𝟗 = 𝟑 YA=aXA mod q=105 mod 19=3
-
Alice 的公钥对为: { 𝒒 , a , 𝒀 𝑨 } = { 𝟏 𝟗 , 𝟏 𝟎 , 𝟑 } \{𝒒,a,𝒀_𝑨\}=\{𝟏𝟗,𝟏𝟎,𝟑\} {q,a,YA}={19,10,3}
-
Bob 生成一个整数 k = 6 k=6 k=6( k < q k<q k<q)
-
收到Alice的公钥{19,10,3},计算密钥 𝑲 = ( 𝒀 𝑨 ) 𝒌 𝒎 𝒐 𝒅 𝒒 = 𝟑 𝟔 𝒎 𝒐 𝒅 𝟏 𝟗 = 𝟕 𝑲=(𝒀_𝑨)^𝒌 \ 𝒎𝒐𝒅 \ 𝒒 =𝟑^𝟔 \ 𝒎𝒐𝒅 \ 𝟏𝟗 = 𝟕 K=(YA)k mod q=36 mod 19=7
-
Alice的公钥{19,10,3}
-
Bob 要给Alice发送消息M=17,因此计算
-
𝑪 𝟏 = a 𝒌 𝒎 𝒐 𝒅 𝒒 = 𝟏 𝟎 𝟔 𝒎 𝒐 𝒅 𝟏 𝟗 = 𝟏 𝟏 𝑪_𝟏=a^𝒌 \ 𝒎𝒐𝒅 \ 𝒒 =𝟏𝟎^𝟔 \ 𝒎𝒐𝒅 \ 𝟏𝟗=𝟏𝟏 C1=ak mod q=106 mod 19=11
-
𝑪 𝟐 = 𝑲 𝑴 𝒎 𝒐 𝒅 𝒒 = 𝟕 × 𝟏 𝟕 𝒎 𝒐 𝒅 𝟏 𝟗 = 𝟓 𝑪_𝟐=𝑲𝑴 \ 𝒎𝒐𝒅 \ 𝒒 =𝟕×𝟏𝟕 \ 𝒎𝒐𝒅 \ 𝟏𝟗=𝟓 C2=KM mod q=7×17 mod 19=5
-
Bob 将密文 𝑪 𝟏 、 𝑪 𝟐 𝑪_𝟏、𝑪_𝟐 C1、C2发送给Alice
-
Alice 根据 𝑪 𝟏 𝑪_𝟏 C1计算密钥 𝑲 = ( 𝑪 𝟏 ) 𝑿 𝑨 𝒎 𝒐 𝒅 𝒒 = 𝟕 𝑲=(𝑪_𝟏)^{𝑿_𝑨} \ 𝒎𝒐𝒅 \ 𝒒=𝟕 K=(C1)XA mod q=7
-
根据 𝑪 𝟐 𝑪_𝟐 C2还原消息 𝑴 = ( 𝑪 𝟐 𝑲 − ) 𝒎 𝒐 𝒅 𝒒 = 𝟏 𝟕 𝑴=(𝑪_𝟐 𝑲^− ) \ 𝒎𝒐𝒅 \ 𝒒=𝟏𝟕 M=(C2K−) mod q=17
练习题
已知B要给A发送消息5,使用ElGamal加密,k=4,q=13,a=2,A的私钥为3,给出密钥K、密文C1与密文C2。
答:已知 M = 5 , k = 4 , q = 13 , a = 2 , X A = 3 M=5, k=4, q=13, a=2, X_A=3 M=5,k=4,q=13,a=2,XA=3
Y A = a X A m o d q = 2 3 m o d 13 = 8 Y_A=a^{X_A} \ mod \ q = 2^3 \ mod \ 13 = 8 YA=aXA mod q=23 mod 13=8
K = ( Y A ) k m o d q = 8 4 m o d 13 = 1 K = (Y_A)^k \ mod \ q = 8^4 \ mod \ 13 = 1 K=(YA)k mod q=84 mod 13=1
C 1 = a k m o d q = 2 4 m o d 13 = 3 C_1 = a^k \ mod \ q = 2^4 \ mod \ 13 = 3 C1=ak mod q=24 mod 13=3
C 2 = K M m o d q = ( 1 × 5 ) m o d 13 = 5 C_2 = KM \ mod \ q = (1×5) \ mod \ 13 = 5 C2=KM mod q=(1×5) mod 13=5
🕒 8. Hash 函数
- Hash 函数,也称散列函数
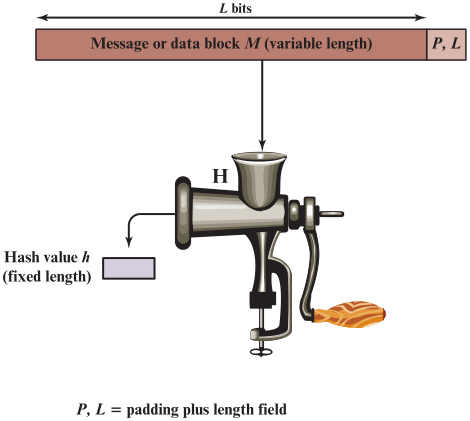
- 可以将可变长度的数据块M 作为输入,产生一个固定长度的Hash值
𝒉 = 𝑯 ( 𝑴 ) 𝒉=𝑯(𝑴) h=H(M)
🕘 8.1 Hash 函数的应用
🕤 8.1.1 消息认证
- 消息认证 是用来验证消息完整性的一种机制;
- 确保接收方Alice收到的数据确实和发送方Bob发出的数据一样,没有非授权的修改、插入、删除和重放;
- 消息认证 还要对发送方声称的身份进行认证;
- 当Hash 用于消息认证时,Hash值也称为消息摘要
方法一:消息
M
M
M与哈希值
H
(
M
)
H(M)
H(M)均对称加密并传输
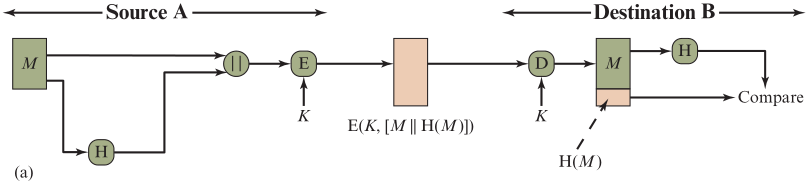
- A给B发送消息𝑴 , 𝑴的Hash值为𝑯(𝑴),拼接得 𝑴 ∥ 𝑯 ( 𝑴 ) 𝑴∥𝑯(𝑴) M∥H(M)
- 使用密钥𝑲 与 对称加密算法𝑬 为数据加密,生成 𝑬 ( 𝑲 , 𝑴 ∥ 𝑯 ) 𝑬( 𝑲,𝑴∥𝑯 ) E(K,M∥H)
- B 收到密文后,使用只有双方共享的密钥𝑲 解密,确认了消息一定来源于 A
- 解密得到 𝑴 ∥ 𝑯 ( 𝑴 ) 𝑴∥𝑯(𝑴) M∥H(M),再次使用Hash 对𝑴 进行计算,得到的值必然是𝑯(𝑴),确认了消息未被更改
❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页
方法二:只对称加密哈希值并传输
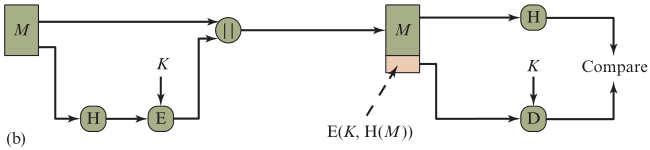
- A给B发送消息𝑴 , 𝑴的Hash值为𝑯(𝑴),加密得 𝑬 ( 𝑲 , 𝑯 ( 𝑴 ) ) 𝑬( 𝑲, 𝑯(𝑴) ) E(K,H(M))
- 将加密后的Hash值 拼接在消息𝑴 后,一起发出 𝑴 ∥ 𝑬 ( 𝑲 , 𝑯 ( 𝑴 ) ) 𝑴∥𝑬( 𝑲, 𝑯(𝑴) ) M∥E(K,H(M))
- B 收到后,对后n位数据使用只有双方共享的密钥𝑲 解密,得到了Hash值,并且只有B 才能看到 Hash值
- 若对消息𝑴 进行计算得到的值与该Hash值相同,确认了消息未发生篡改
方法三:双方共享校验值
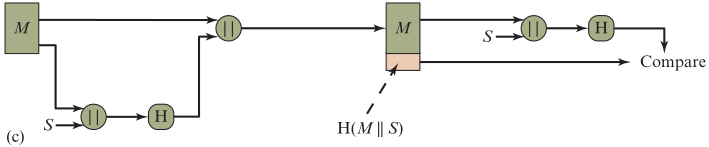
- 通信双方共享一个秘密值S
- A 将消息M 和秘密值S 串联后,计算其Hash值,并将得到的Hash值 附在消息M 后发送给B
- B 收到后,将双方预先知道的秘密值S 拼在M后,计算出Hash值,若与接收到的Hash值相同,说明消息未篡改
- 秘密值S 本身没有在信道中传送
方法四:消息
M
M
M与哈希值
H
(
M
)
H(M)
H(M)均对称加密并加入校验值

- 在方案三的基础上,使用双方共享的密钥K与对称加密算法E 来为消息M 与Hash值H 一起加密
- 即保证了消息的保密性,也保证了完整性
🕤 8.1.2 数字签名
方法一:非对称加密哈希值并传输
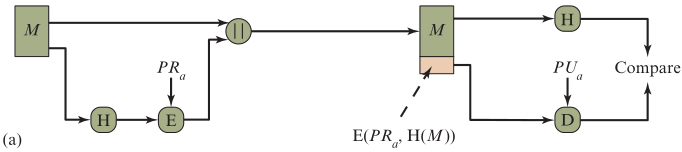
- A给B发送消息𝑴 , 𝑴的Hash值为𝑯(𝑴),加密得 𝑬 ( 𝑷 𝑹 𝑨 , 𝑯 ( 𝑴 ) ) 𝑬( 𝑷𝑹_𝑨,𝑯(𝑴) ) E(PRA,H(M)),注意是发送方的私钥
- 将加密后的Hash值 拼接在消息𝑴 后,一起发出
- B 收到后,对消息𝑴 计算其Hash值
- 使用发送方A的公钥 𝑷 𝑼 𝑨 𝑷𝑼_𝑨 PUA 来解密后半部分,得到了原始Hash值,若二者相同说明消息未被篡改
方法二:

- 若既要保证消息的完整性,又要保证消息的保密性,可以在数字签名的基础上为 消息M 和 加密Hash值 一起使用密钥K 进行对称加密
🕘 8.2 安全需求
-
可变输入
Hash函数 可应用于任意大小的数据块 -
固定长度
Hash函数 产生的是固定长度的输出 -
计算效率
对任意消息x,计算H(x)容易,硬件软件均可实现 -
抗原像攻击
对于Hash值 𝒉=𝑯(𝒙) ,称𝒙是𝒉的原像
给定𝒉,找到满足𝒉=𝑯(𝒙) 的 𝒙 在计算上不可行,即不能通过哈希值反推出明文 -
抗弱碰撞
对任意给定的𝒙,找到满足𝒚≠𝒙 且𝑯(𝒚)=𝑯(𝒙)的𝒚,在计算上不可行,即已知一个明文与其哈希值,不能找到另一个哈希值与这个已知明文的哈希值相等的明文 -
抗强碰撞(生日攻击)
找到任何满足𝑯(𝒚)=𝑯(𝒙)的偶对(𝒙,𝒚),在计算上不可行,即不能同时找到两个消息而且它们的哈希值相等
抗原像 抗弱碰撞 抗强碰撞 Hash数字签名 Y Y Y 入侵检测、病毒检测 Y 单向口令文件 Y \begin{array}{|c|c|c|c|} \hline & \text { 抗原像 } & \text { 抗弱碰撞 } & \text { 抗强碰撞 } \\ \hline \text { Hash数字签名 } & Y & Y & Y \\ \hline \text { 入侵检测、病毒检测 } & & Y & \\ \hline \text { 单向口令文件 } & Y & & \\ \hline \end{array} Hash数字签名 入侵检测、病毒检测 单向口令文件 抗原像 YY 抗弱碰撞 YY 抗强碰撞 Y
🕘 8.3 安全Hash算法
SHA-1 SHA-224 SHA-256 SHA-512 SHA- 512 / 224 SHA- 512 / 256 消息摘要长度(即哈希值长度) 160 224 256 512 224 256 消息长度 < 2 64 < 2 64 < 2 64 < 2 128 < 2 128 < 2 128 分组长度 512 512 512 1024 1024 1024 字长度 32 32 32 64 64 64 \begin{array}{|l|l|l|l|l|l|l|} \hline & \text { SHA-1 } & \text { SHA-224 } & \text { SHA-256 } & \text { SHA-512 } & \begin{array}{l} \text { SHA- } \\ 512 / 224 \end{array} & \begin{array}{l} \text { SHA- } \\ 512 / 256 \end{array} \\ \hline \text { 消息摘要长度(即哈希值长度)} & 160 & 224 & 256 & 512 & 224 & 256 \\ \hline \text { 消息长度 } & <2^{64} & <2^{64} & <2^{64} & <2^{128} & <2^{128} & <2^{128} \\ \hline \text { 分组长度 } & 512 & 512 & 512 & 1024 & 1024 & 1024 \\ \hline \text { 字长度 } & 32 & 32 & 32 & 64 & 64 & 64 \\ \hline \end{array} 消息摘要长度(即哈希值长度) 消息长度 分组长度 字长度 SHA-1 160<26451232 SHA-224 224<26451232 SHA-256 256<26451232 SHA-512 512<2128102464 SHA- 512/224224<2128102464 SHA- 512/256256<2128102464
🕘 8.4 SHA-512
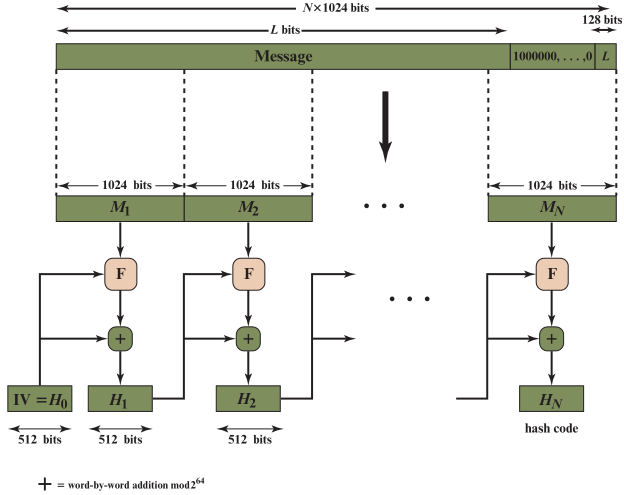
🕤 8.4.1 附加填充位(步骤1)

- 要处理消息𝑴,长度𝑳 bits
- 在消息𝑴后 增加 填充内容𝑷,使得填充后的长度 𝑳 𝑴 + 𝑳 𝑷 = 𝟖 𝟗 𝟔 ( 𝒎 𝒐 𝒅 𝟏 𝟎 𝟐 𝟒 ) 𝑳_𝑴+𝑳_𝑷=𝟖𝟗𝟔 (𝒎𝒐𝒅 𝟏𝟎𝟐𝟒) LM+LP=896(mod1024)
- 即使消息𝑴的长度已满足要求,仍需要进行填充
- 填充的位数在 1~1024 之间,填充内容为1和一串连续0
🕤 8.4.2 附加长度位(步骤2)
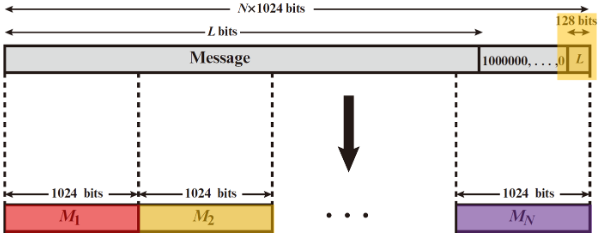
- 在填充内容𝑷 之后附加一个128位的块,用来放消息𝑴的长度𝑳
- 在该块中,将长度𝑳放在低位上,其余高位为空则放0
- 经过填充,消息长度为 N ∗ 1024 N*1024 N∗1024,将其划分为一个个1024位的分组 𝑴 𝟏 , 𝑴 𝟐 , . . . . 𝑴 𝑵 𝑴_𝟏,𝑴_𝟐,.... 𝑴_𝑵 M1,M2,....MN
练习:
使用SHA-512算法,计算消息36的Hash值,问:
(1)消息长度是多少个bit?
(2)填充内容P 是什么?
(3)消息长度区域L 是什么?
(4)生成的Hash长度是什么?
答:
(1) 𝑴 = 𝟑 𝟔 𝑴=𝟑𝟔 M=36,化二进制为:100100,因此消息𝑴的长度是6个bit
(2) 𝑳 𝑴 + 𝑳 𝑷 = 𝟖 𝟗 𝟔 ( 𝒎 𝒐 𝒅 𝟏 𝟎 𝟐 𝟒 ) 𝑳_𝑴+𝑳_𝑷=𝟖𝟗𝟔 (𝒎𝒐𝒅 𝟏𝟎𝟐𝟒) LM+LP=896(mod1024)
𝟔 + 𝑳 𝑷 = 𝟖 𝟗 𝟔 ( 𝒎 𝒐 𝒅 𝟏 𝟎 𝟐 𝟒 ) 𝟔+𝑳_𝑷=𝟖𝟗𝟔 (𝒎𝒐𝒅 𝟏𝟎𝟐𝟒) 6+LP=896(mod1024)
𝑳 𝑷 = 𝟖 𝟗 𝟎 ( 𝒎 𝒐 𝒅 𝟏 𝟎 𝟐 𝟒 ) = 𝒏 × 𝟏 𝟎 𝟐 𝟒 + 𝟖 𝟗 𝟎 𝑳_𝑷=𝟖𝟗𝟎 (𝒎𝒐𝒅 𝟏𝟎𝟐𝟒)=𝒏×𝟏𝟎𝟐𝟒+𝟖𝟗𝟎 LP=890(mod1024)=n×1024+890
令 𝑳 𝑷 = 𝟖 𝟗 𝟎 𝑳_𝑷=𝟖𝟗𝟎 LP=890(即n取0),填充内容 𝑷 𝑷 P:1和889个0
(3) 𝑴 = 𝟑 𝟔 𝑴=𝟑𝟔 M=36,继续填充 消息长度区域,消息长度为6,化为二进制110,将其放在 消息长度区域 的最低3位,其余高位填充为0,共128位
即消息长度区域为 125个0 和 110
(4)生成的Hash长度是512位(64字节)
🕤 8.4.3 缓冲区初始化(步骤3)
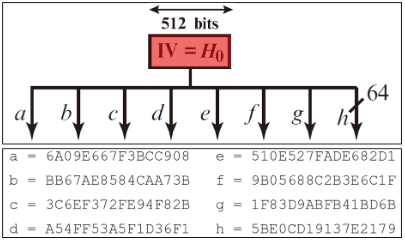
- Hash函数的 中间结果 和 最终结果 都保存在一个512位的缓存区中
- 512位缓存区 用8个64位的寄存器abcdefgh共同表示
- 将寄存器abcdefgh 进行初始化,对前8个素数开平方,取小数部分的前64位
🕤 8.4.4 分组处理(步骤4)
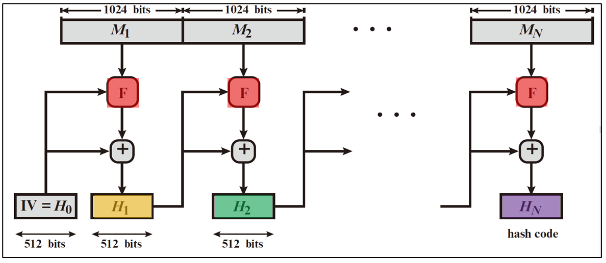
- SHA-512算法的核心是具有 80轮运算 的迭代函数F
- 用函数F依次处理各分组,最终的输出即为消息的Hash
🕒 9. 消息认证码
🕘 9.1 消息认证函数
🕤 9.1.1 Hash
- Hash函数 将任意长的消息 映射为 固定长度的Hash值,以该值作为消息的认证符
🕤 9.1.2 加密
- 对整个消息加密,产生的密文作为消息的认证符
🕤 9.1.3 MAC
消息认证码MAC 是关于消息和密钥的函数,产生固定长度的值作为认证符
🕘 9.2 基于Hash函数的MAC——HMAC
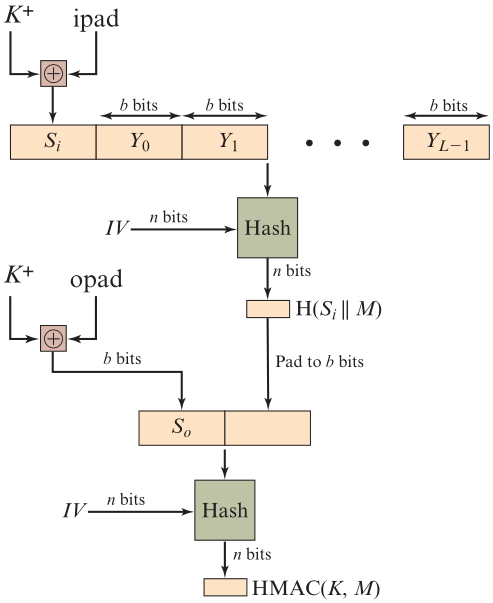
- 在密钥 K K K 左边填充0,得到 b b b位的 K + K^+ K+
- 构造 i p a d = 00110110 ipad = 00110110 ipad=00110110 重复 b / 8 b/8 b/8次,使其和 K + K+ K+等长
- 将 K + K^+ K+ 与 i p a d ipad ipad 进行按位异或,产生分组 S i S_i Si
- 将填充内容 P P P、长度块 L L L附加在消息之后,变为分组长度 b b b 的整数倍
- 将填充后的消息 M M M 附加在 S i S_i Si之后
- 将 ( S i + M ) (S_i+M) (Si+M)、初始值 I V IV IV 一起输入到选定的Hash函数中,产生Hash值 H ( S i + M ) H(Si+M) H(Si+M)
- 构造 o p a d = 01011100 opad = 01011100 opad=01011100 重复 b / 8 b/8 b/8次
- 将 K + K+ K+ 与 o p a d opad opad 进行按位异或,产生分组 S o S_o So
- 将前面得到的Hash值 填充至 b b b位,附加在 S o S_o So 后面
- 将 ( S o + H ) (S_o+H) (So+H)、初始值 I V IV IV 一起输入到选定的Hash函数中,产生的Hash值 即 消息认证码HMAC
练习题:
现在Hash函数是将所有分组进行按位异或,且分组长度b=8,填充内容P为10…00,消息长度区域共2位。
若密钥K=110,请给出消息001的HMAC。
解答: K + = 00000110 K^+ =00000110 K+=00000110
i p a d = 00110110 o p a d = 01011100 ipad = 00110110 \qquad opad = 01011100 ipad=00110110opad=01011100
S i = K + ⊕ i p a d = 00110000 S_i = K^+\oplus ipad = 00110000 Si=K+⊕ipad=00110000
Y = 001 100 11 Y = 001 \ 100 \ 11 Y=001 100 11(明文分组)
H 1 = H ( S i ∣ ∣ Y ) = S i ⊕ Y = 00000011 H_1=H(S_i \mid\mid Y) = S_i \oplus Y = 00000011 H1=H(Si∣∣Y)=Si⊕Y=00000011
S 0 = K + ⊕ o p a d = 01011010 S_0 = K^+\oplus opad = 01011010 S0=K+⊕opad=01011010
H 2 = H ( S 0 ∣ ∣ H 1 ) = S 0 ⊕ H 1 = 01011001 H_2=H(S_0 \mid\mid H_1) = S_0 \oplus H_1 = 01011001 H2=H(S0∣∣H1)=S0⊕H1=01011001
🕒 10. 数字签名
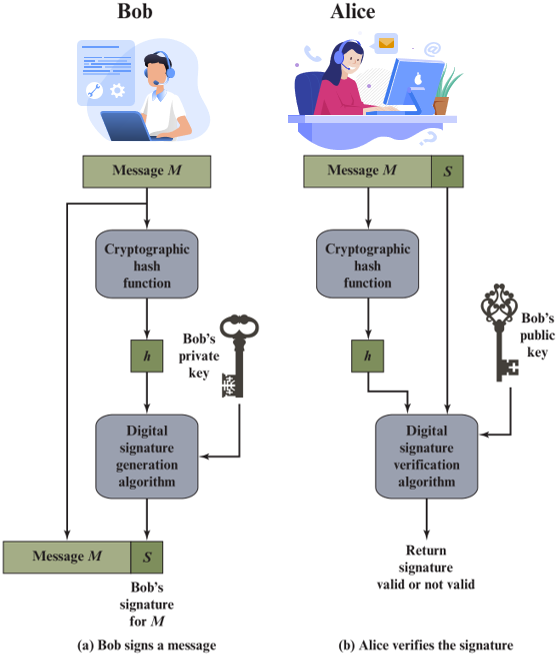
练习题:
已知Alice要为一个Hash值为2的消息制作数字签名,使用ElGamal数字签名方案,她选取q=11,a=2,私钥为4,K=3。
请给出S1、S2;
答: m = 2 , q = 11 , a = 2 , X A = 4 , K = 3 m=2,q=11,a=2,X_A=4,K=3 m=2,q=11,a=2,XA=4,K=3
S 1 = a K m o d q = 2 3 m o d 11 = 8 S1=a^K \ mod \ q = 2^3 \ mod \ 11=8 S1=aK mod q=23 mod 11=8
q − 1 = 11 − 1 = 10 q-1=11-1=10 q−1=11−1=10
q − 1 K q ′ d ′ x y 10 3 3 1 1 − 3 3 1 3 1 0 1 1 0 1 1 0 \begin{array}{|c|c|c|c|c|c|} \hline q-1 & K & q^{\prime} & d^{\prime} & x & y \\ \hline 10 & 3 & 3 & 1 & 1 & -3 \\ \hline 3 & 1 & 3 & 1 & 0 & 1 \\ \hline 1 & 0 & & 1 & 1 & 0 \\ \hline \end{array} q−11031K310q′33d′111x101y−310
K − 1 = − 3 m o d 10 = 7 K^{-1}=-3 \ mod \ 10=7 K−1=−3 mod 10=7
S 2 = K − 1 ( m − X A S 1 ) m o d ( q − 1 ) S2=K^{-1}(m-X_AS1) \ mod \ (q-1) S2=K−1(m−XAS1) mod (q−1)
= 7 × ( 2 − 4 × 8 ) m o d 10 = 0 =7×(2-4×8) \ mod \ 10 = 0 =7×(2−4×8) mod 10=0
OK,以上就是密码学的期末复习啦~~ ,感谢友友们的阅读,祝大家逢考必过哦~~
💫如果有错误❌,欢迎批评指正呀👀~让我们一起相互进步🚀
🎉如果觉得收获满满,可以点点赞👍支持一下哟~
❗ 转载请注明出处
作者:HinsCoder
博客链接:🔎 作者博客主页








![(Java)[NOIP2006 普及组] 明明的随机数](https://img-blog.csdnimg.cn/6f77d97068c9475797df210e5a31a37c.png)