【SVM时序预测】基于matlab粒子群算法优化支持向量机PSO-SVM期贷时序数据预测【含Matlab源码 2289期】

news2024/9/21 18:37:19

⛄一、PSO-SVM介绍

1 SVM
SVM是Vapnik提出的一种分类技术，这一技术具有坚实的统计理论基础。SVM可以将原始的数据映射到高维且线性可分的空间，扩展了线性不可分的样本数据，它是使用核函数将线性不可分转换为线性可分。

如果问题为线性不可分割，则需要引入非线性变换。在变换后的坐标空间中，划分超平面的模型方程如下

f(x)=ωTφ(x)+b (5)

式中：ω和b为SVM模型中的参数，φ(x)表示x的映射变换。为了使得找到的超平面到不同类别之间的距离和最大，则有
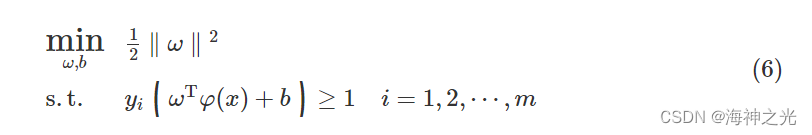
在这里插入图片描述
根据二次规划技术结合核函数进行求解得到超平面的方程

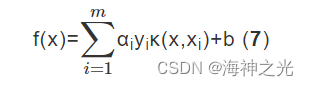
式中：κ(·)为核函数，κ(x,xi)表示ϕ(x)·ϕ(xi),ϕ(x)表示关于x的映射变换，αi表示权重系数，yi表示真实值。核函数技术是使用原来的样本数据计算变换后的空间中相似度的一种方法，可以用来帮助处理SVM中的非线性问题。常用的核函数有径向基函数、线性核函数、多项式核函数等。本文采用径向基核函数。

SVM分类模型中存在两个非常重要的参数C和γ。参数C代表惩罚因子，C的取值会影响分类器的分类精度，也可以理解为对误差的容忍限度。如果C太大，则训练阶段的分类准确率很高，而测试阶段的分类准确率很低，对于模型产生的误差具有较低的容忍程度。如果C太小，则分类准确率较差，不能令人满意，对于模型产生的误差具有较高的容忍程度，从而使得训练出来的分类模型变得无用。不恰当的C值会导致模型具有较差的泛化能力。参数γ对结果的影响相较于惩罚因子更大，γ的取值会对特征空间中的划分产生影响。如果γ的值过大会导致拟合过度，而γ的值过小会导致拟合不足，并且γ的大小会影响支持向量的多少，从而影响模型的训练速度。因此C和γ的取值对于SVM的影响很大，不同的取值会导致不同的分类性能，为了选择合适的C和γ的值，通过PSO优化SVM模型。

2 PSO算法
PSO算法是基于种群的搜索算法。在群体中粒子的经验知识会影响相邻粒子的运动趋势。PSO算法中的任意一个粒子均为潜在的优化解，通过不断地调整自身位置找到设置条件下的相对更优解。

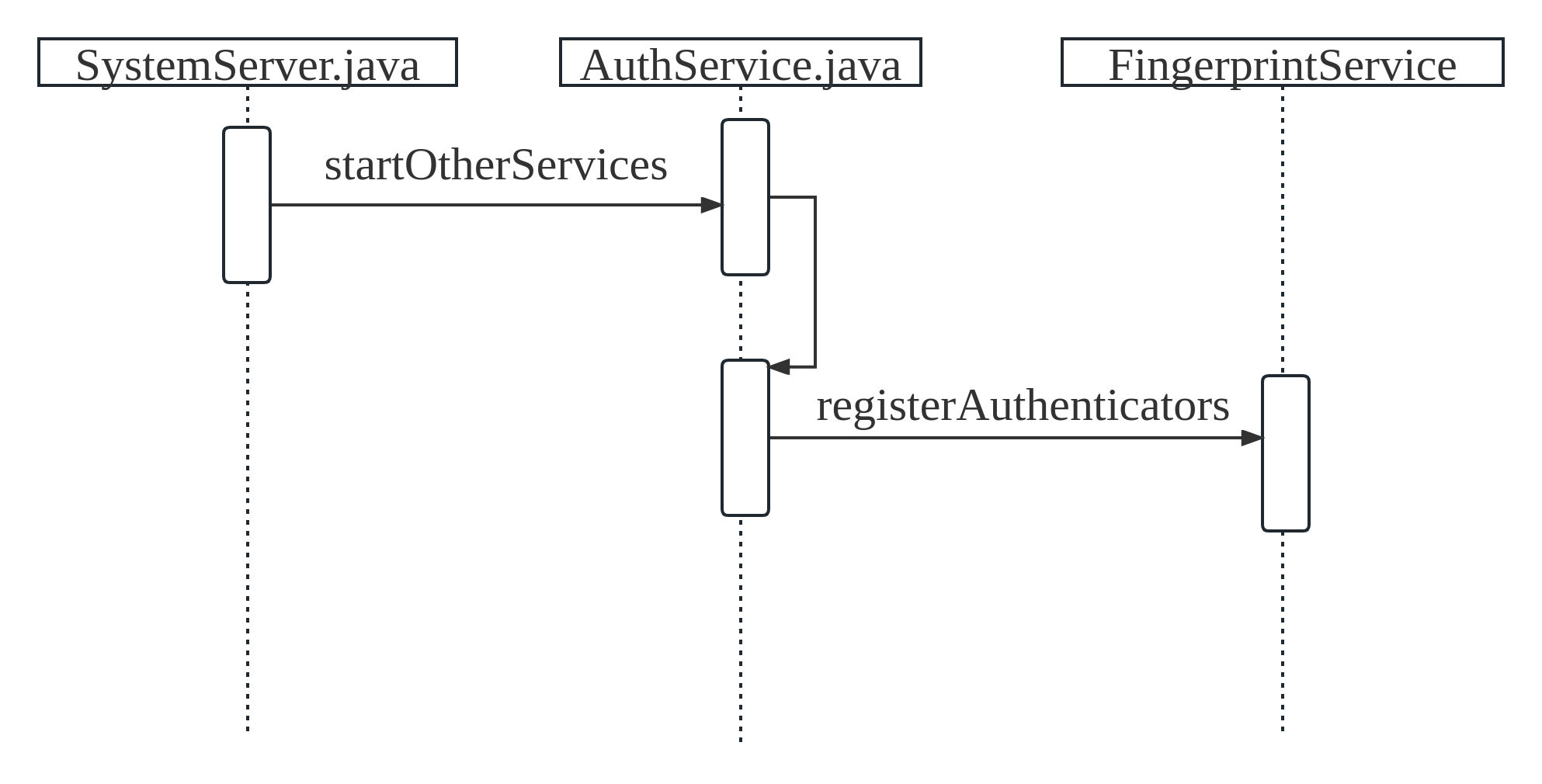
粒子群优化算法由改变每个粒子向其pbest和gbest位置移动的速度组成。加速度由随机项加权得到，在这些随机项中，为向pbest和gbest位置的加速度生成单独的随机数。PSO更新每个粒子的位置、速度的方式见式(8)
在这里插入图片描述
式中：w1表示初始的设置值，we表示迭代到最大的进化代时的设置值，Ik表示设置的最大的迭代次数，g表示当前迭代次数。通过LDW方法可以提高PSO的寻优性能。

3 粒子群优化的支持向量机
在本节中，阐述了用于停电预测的PSO-SVM算法模型。利用LDW优化的粒子群算法寻找参数的最佳值，自动求解支持向量机的模型选择问题，从而优化SVM分类器的精度。在PSO算法中，粒子在搜索空间中位置的变化是基于个体追随他人成功的社会心理倾向。群中一个粒子的变化受其邻居的经验或知识的影响。因此，搜索过程使得粒子随机返回到搜索空间中先前成功的区域。

为了实现本文提出的方法，将径向基核函数(Radial basis kernel function, RBF)用于支持向量机分类器。将粒子群中每个粒子的位置视为一个矢量，这个矢量编码SVM分类器的两个参数的值，分别是核参数C和γ。分类精度是设计适应度函数的一个标准。因此，对于分类精度高的粒子产生较高的适应值。同时为了更好地利用粒子群算法寻优，采用线性递减权重动态更新w的值。最终将粒子群优化的SVM模型应用于停电情况的预测。粒子群优化的SVM算法的算法描述如下：
在这里插入图片描述
算法1是通过粒子群优化算法优化支持向量机中的参数，提高支持向量机模型的性能。首先初始化，随机生成初始的粒子，并对生成的粒子进行评估，给局部最优和全局最优的位置赋值(第1～7行)。接着，通过线性递减权重更新粒子的惯性因子值，接着更新粒子的速度和位置值，并对粒子进行评估，将不同粒子的位置对应的参数代入SVM模型中得到分类精度，根据不同参数下的分类精度更新局部最优和全局最优的位置，然后不断迭代直到满足结束条件。最后，返回搜索到的适合停电数据预测的SVM模型下的相对更优参数(第8～24行)。

⛄二、部分源代码

%% 清空环境
tic;clc;clear;close all;format compact
%% 加载数据
data=xlsread(‘EUA五分钟.xlsx’,‘G2:G30763’); save data data
load data
% 归一化
[a,inputns]=mapminmax(data’,0,1);%归一化函数要求输入为行向量
data_trans=data_process(5,a);%% 对时间序列预测建立滚动序列，即用1到m个数据预测第m+1个数据，然后用2到m+1个数据预测第m+2个数据
input=data_trans(:,1:end-1);
output=data_trans(:,end);
%% 数据集前75%训练后25%预测
m=round(size(data_trans,1)*0.75);
Pn_train=input(1:m,:);
Tn_train=output(1:m,:);
Pn_test=input(m+1:end,:);
Tn_test=output(m+1:end,:);

%% 1.没有优化的SVM
bestc=0.001;bestg=10;%c和g随机赋值表示没有优化的SVM
t=0;%t=0为线性核函数,1-多项式。2rbf核函数
cmd = [‘-s 3 -t ‘,num2str(t),’ -c ‘, num2str(bestc),’ -g ‘,num2str(bestg),’ -p 0.01 -d 1’];

model = svmtrain(Tn_train,Pn_train,cmd);%训练
[predict,~]= svmpredict(Tn_test,Pn_test,model);%测试
% 反归一化，为后面的结果计算做准备
predict0=mapminmax(‘reverse’,predict’,inputns);%测试实际输出反归一化
T_test=mapminmax(‘reverse’,Tn_test’,inputns);%测试集期望输出反归一化
T_train=mapminmax(‘reverse’,Tn_train’,inputns);%训练集期望输出反归一化

figure
plot(predict0,‘r-’)
hold on;grid on
plot(T_test,‘b-’)
xlabel(‘样本编号’)
ylabel(‘收盘价/元’)
if t0
title(‘线性核SVM预测’)
elseif t1
title(‘多项式核SVM预测’)
else
title(‘RBF核SVM预测’)
end