作者：一个喜欢猫咪的的程序员 

专栏：《数据结构》

喜欢的话：世间因为少年的挺身而出，而更加瑰丽。                                  ——《人民日报》

---

目录

堆排序：（以小堆为例）

 Heapsort函数（堆排序）：

向下调整具体的时间复杂度：

向上调整具体的时间复杂度：

如何实现堆排序

TOP-K问题：

---

堆排序：（以小堆为例）

堆的分类：

• 升序or降序
• 大堆or小堆

void test2()
{//堆排序
	int array[] = { 27,15,19,18,28,34,65,49,25,37 };
	Heapsort(array, sizeof(array) / sizeof(array[0]));
	for (int i = 0; i < sizeof(array) / sizeof(array[0]); i++)
	{
		printf("%d ", array[i]);
	}
	printf("\n");

}

 Heapsort函数（堆排序）：

int array[] = { 27,15,19,18,28,34,65,49,25,37 };

需将这个数组进行大堆排列，分为两种调整形式：向上调整和向下调整。

向上调整和向下调整的思想可以参考我的例外一篇博客：http://t.csdn.cn/YFSpd

void Ajustup(HPDataType*a, int child)
{//N*logN
	assert(a);
	//int child = n - 1;
	while (child > 0)
	{
		int parent = (child - 1) / 2;
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
		}
		else
		{
			break;
		}
	}
}
void Ajustdown(HPDataType* a, int n,int parent)
{//O(N)
	assert(a);
	int child = 2 * parent+1;
	while (child<n)
	{
		if (child + 1 < n && a[child] < a[child + 1])//  <假设左子树大
		{
			child++;
		}
		if (a[child] > a[parent])//>大堆，<为小堆
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = child * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

 向上调整和向下调整具体的时间复杂度是多少呢？

向下调整具体的时间复杂度：

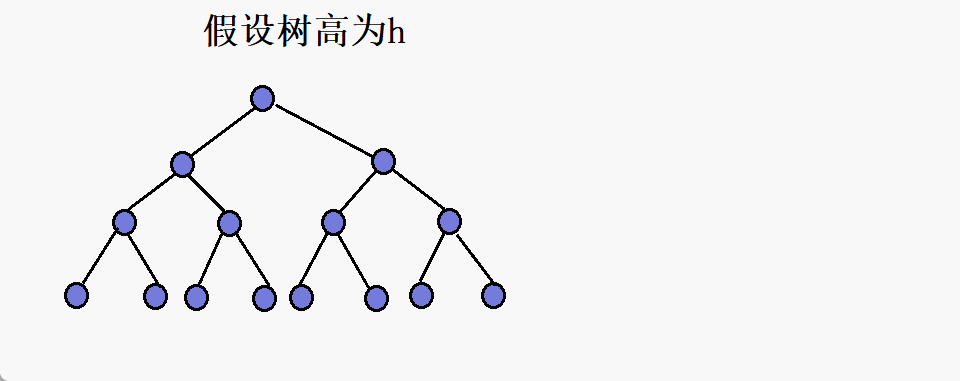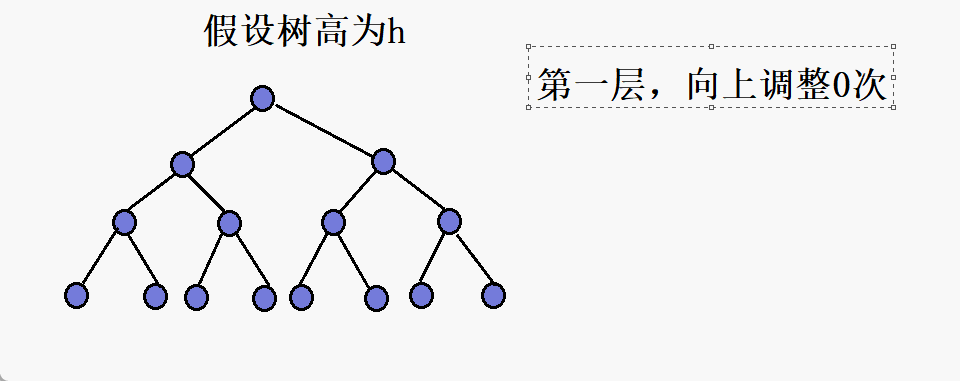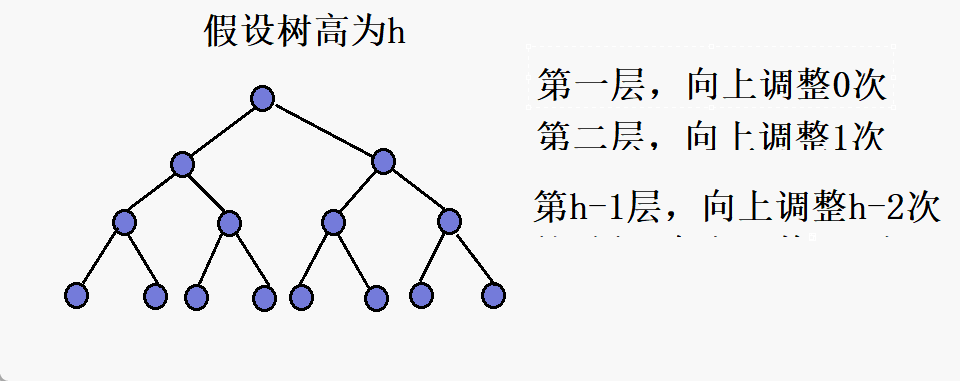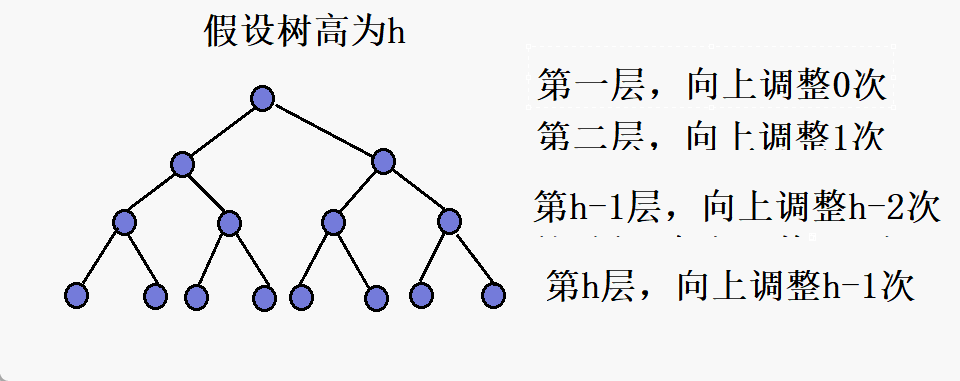
假设树高为h

第h层，有2^(h-1）个节点，需要向下调整0次（直接不算，从第h-1层开始算）。

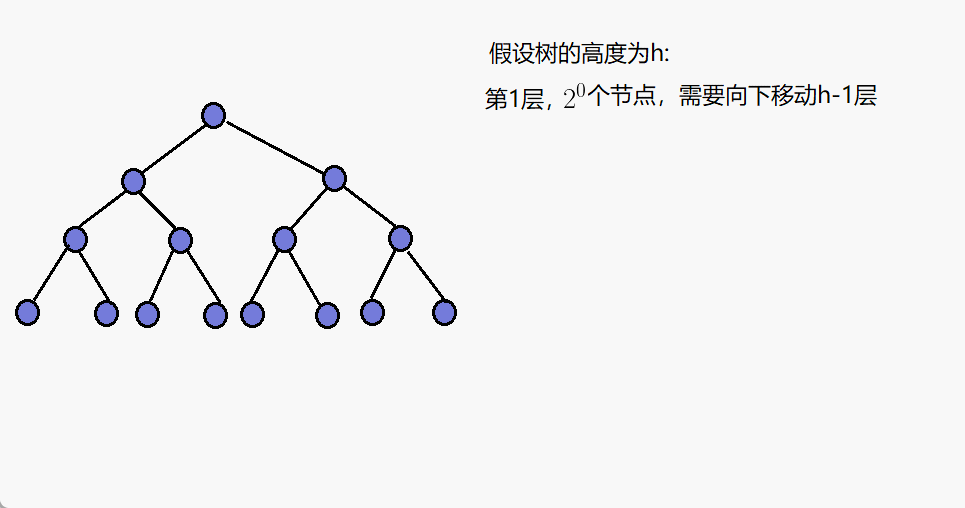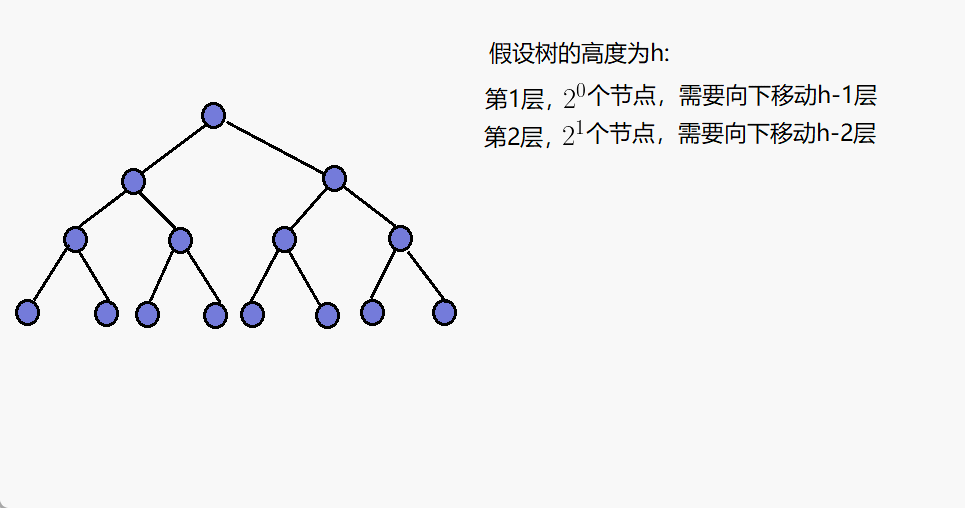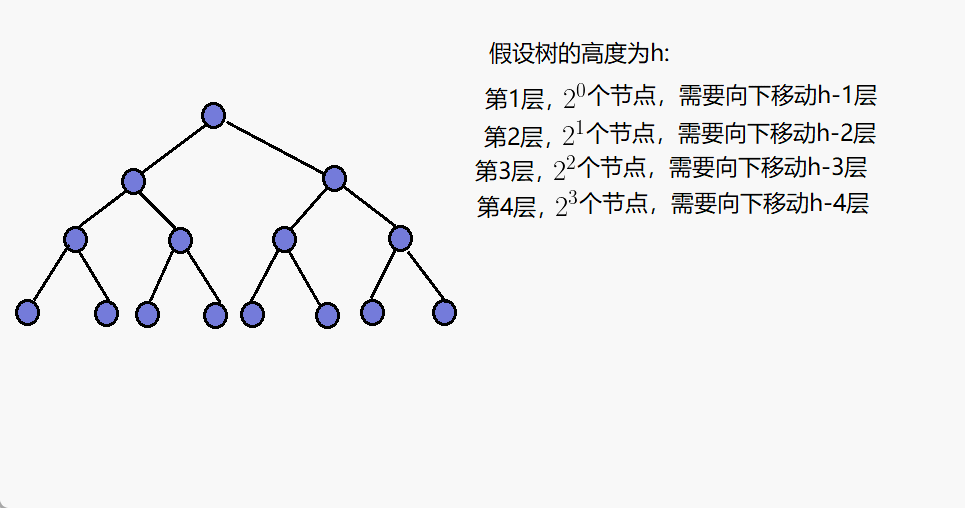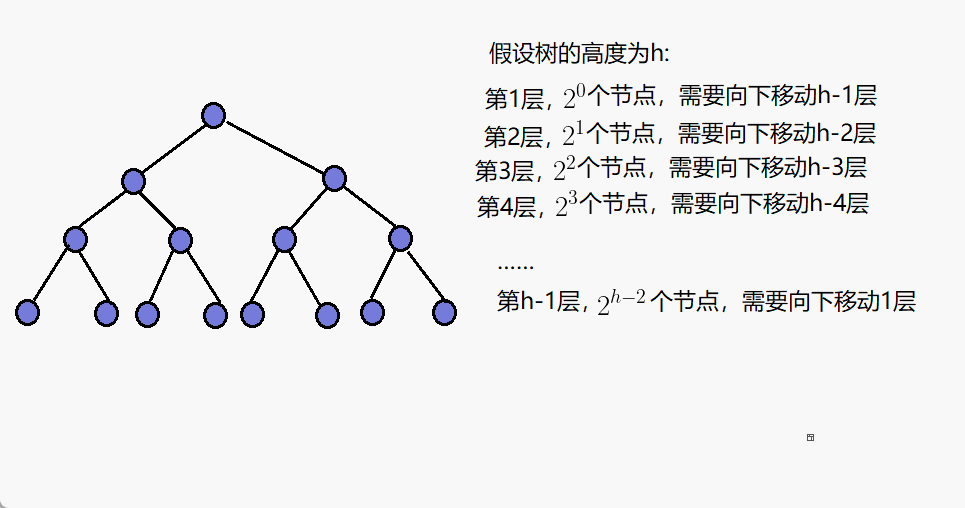
第h-1层，有2^（h-2）个节点，需要向下调整1层。

第h-2层，有2^（h-3）个节点，需要向下调整2层。

......

第4层，有2^3个节点，需要向下调整h-4层。

第3层，有2^2个节点，需要向下调整h-3层。

第2层，有2^1个节点，需要向下调整h-2层。

第1层，有2^0个节点，需要向下调整h-1层。

当h高的次数，最多调整层数为：

F（h）=2^0*（h-1）+2^1*(h-2)+2^2*(h-3)+...+2^(h-3)*2+2^(h-2)*1+2^(h-1)*0       ——①

2*F（h）=2^1*（h-1）+2^2*(h-2)+2^3*(h-3)+...+2^(h-2)*2+2^(h-1)*1+2^(h)*0       ——②

有错位相减②-①可得：

F（h）=-2^0*（h-1）+2^1+2^2+....+2^(h-2)+2^(h-1)

F（h）=2^h-1-h                                                                                                           ——③

 当树高为h时，节点总个数N为：

N=2^0+2^1+...+2^（h-2）+2^（h-1）

N=2^h-1                                                                                                                        ——④

有④可得：h=log（N+1）                                                                                            ——⑤

综合③④⑤可得：

F（N）=N-log（N+1）

•  因此时间复杂度为O（N）

---

向上调整具体的时间复杂度：

在一层，需要向上调整0次

第二层，向上调整1次

第三层，向上调整2次

...

第h-1层，向上调整h-2次

第h层，向上调整h-1次

F（h）=2^1*1+2^2*2+....+2^(h-1)*(h-1)。

由错位相减可得：

F(N)=2N(1-log(N+1))。

• 时间复杂度为O（N*logN）

如何实现堆排序

显然向下调整优于向上调整。

 先利用Ajustdown排序好数组，然后再用交换Ajustdown实现小堆。

void Heapsort(int*a,int n)//堆排序
{//向上调整
	for (int i = 1; i <n; i++)
	{
		Ajustup(a, i);
	}
	//向下调整
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		Ajustdown(a, n, i);
	}
	int end = n - 1;
	while (end>0)
	{
		Swap(&a[0], &a[end]);
		Ajustdown(a, end, 0);
		end--;
	}
	//N*logN
}
void test2()
{//堆排序
	int array[] = { 27,15,19,18,28,34,65,49,25,37 };
	Heapsort(array, sizeof(array) / sizeof(array[0]));
	for (int i = 0; i < sizeof(array) / sizeof(array[0]); i++)
	{
		printf("%d ", array[i]);
	}
	printf("\n");

}

---

TOP-K问题：

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

当数据量特别大时，我们造一个数组来存储他们依次存储时，就不大现实。

可以先开一个K个空间的数组，将这个数据量的前K个放进去，将他们小堆排列，并将这个数据量每个数与堆顶的元素相比较，比它大就替代它进入数组，在向下排列，以此循环。

void test3()
{
	int minHeap[5];
	FILE* fout = fopen("data.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		exit(-1);
	}
	int k = sizeof(minHeap) / sizeof(minHeap[0]);
	for (int i = 0; i < k; i++)
	{
		fscanf(fout,"%d",&minHeap[i]);
	}
	for (int i = 0; i < sizeof(minHeap) / sizeof(minHeap[0]); i++)
	{//检查是否录入数据
		printf("%d ", minHeap[i]);
	}
	printf("\n");
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		Ajustdown(minHeap, k, i);
	}
	for (int i = 0; i < sizeof(minHeap) / sizeof(minHeap[0]); i++)
	{//检查是否为大小堆
		printf("%d ", minHeap[i]);
	}
	printf("\n");
	int data = 0;
	while (fscanf(fout, "%d", &data) != EOF)
	{
		if (data > minHeap[0])
		{
			minHeap[0] = data;
			Ajustdown(minHeap, k, 0);
		}
	}
	int end = k - 1;
	while (end > 0)
	{
		Swap(&minHeap[0], &minHeap[end]);
		Ajustdown(minHeap, end, 0);
		end--;
	}//完成升序或者降序
	for (int i = 0; i < sizeof(minHeap) / sizeof(minHeap[0]); i++)
	{//检查是否为大小堆
		printf("%d ", minHeap[i]);
	}
	printf("\n");
	fclose(fout);
}
void test4()
{
	int n, k;
	scanf("%d %d", &n, &k);
	FILE* fint = fopen("data1.txt", "w");
	if (fint == NULL)
	{
		perror("fopen fail");
		exit(-1);
	}
	srand(time(0));
	int randK = k;
	for (size_t i = 0; i < n; ++i)
	{
		int data = rand() % 100000;
		fprintf(fint, "%d\n", data);
	}
	fclose(fint);
	int* minHeap = (int*)malloc(sizeof(int) * k);
	FILE* fout = fopen("data1.txt", "r");
	if (fout == NULL)
	{
		perror("fopen fail");
		exit(-1);
	}
	for (int i = 0; i < k; i++)
	{
		fscanf(fout, "%d", &minHeap[i]);
	}
	for (int i = 0; i < k; i++)
	{//检查是否录入数据
		printf("%d ", minHeap[i]);
	}
	printf("\n");
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		Ajustdown(minHeap, k, i);
	}
	for (int i = 0; i < k; i++)
	{//检查是否为大小堆
		printf("%d ", minHeap[i]);
	}
	printf("\n");
	int data = 0;
	while (fscanf(fout, "%d", &data) != EOF)
	{
		if (data > minHeap[0])
		{
			minHeap[0] = data;
			Ajustdown(minHeap, k, 0);
		}
	}
	int end = k - 1;
	while (end > 0)
	{
		Swap(&minHeap[0], &minHeap[end]);
		Ajustdown(minHeap, end, 0);
		end--;
	}//完成升序或者降序
	for (int i = 0; i < k; i++)
	{//检查是否为大小堆，升序或者降序
		printf("%d ", minHeap[i]);
	}
	printf("\n");
	fclose(fout);
}
int main()
{
	//test1();
	test2();
	//test3();
	//test4();
	return 0;
}