有 n 头奶牛，已知它们的身高为 1∼n 且各不相同，但不知道每头奶牛的具体身高。

现在这 n 头奶牛站成一列，已知第 i 头牛前面有 Ai 头牛比它低，求每头奶牛的身高。

输入格式
第 1 行：输入整数 n。

第 2…n 行：每行输入一个整数 Ai，第 i 行表示第 i 头牛前面有 Ai 头牛比它低。
（注意：因为第 1 头牛前面没有牛，所以并没有将它列出）

输出格式
输出包含 n 行，每行输出一个整数表示牛的身高。

第 i 行输出第 i 头牛的身高。

数据范围
1≤n≤105
输入样例：
5
1
2
1
0
输出样例：
2
4
5
3
1

分析

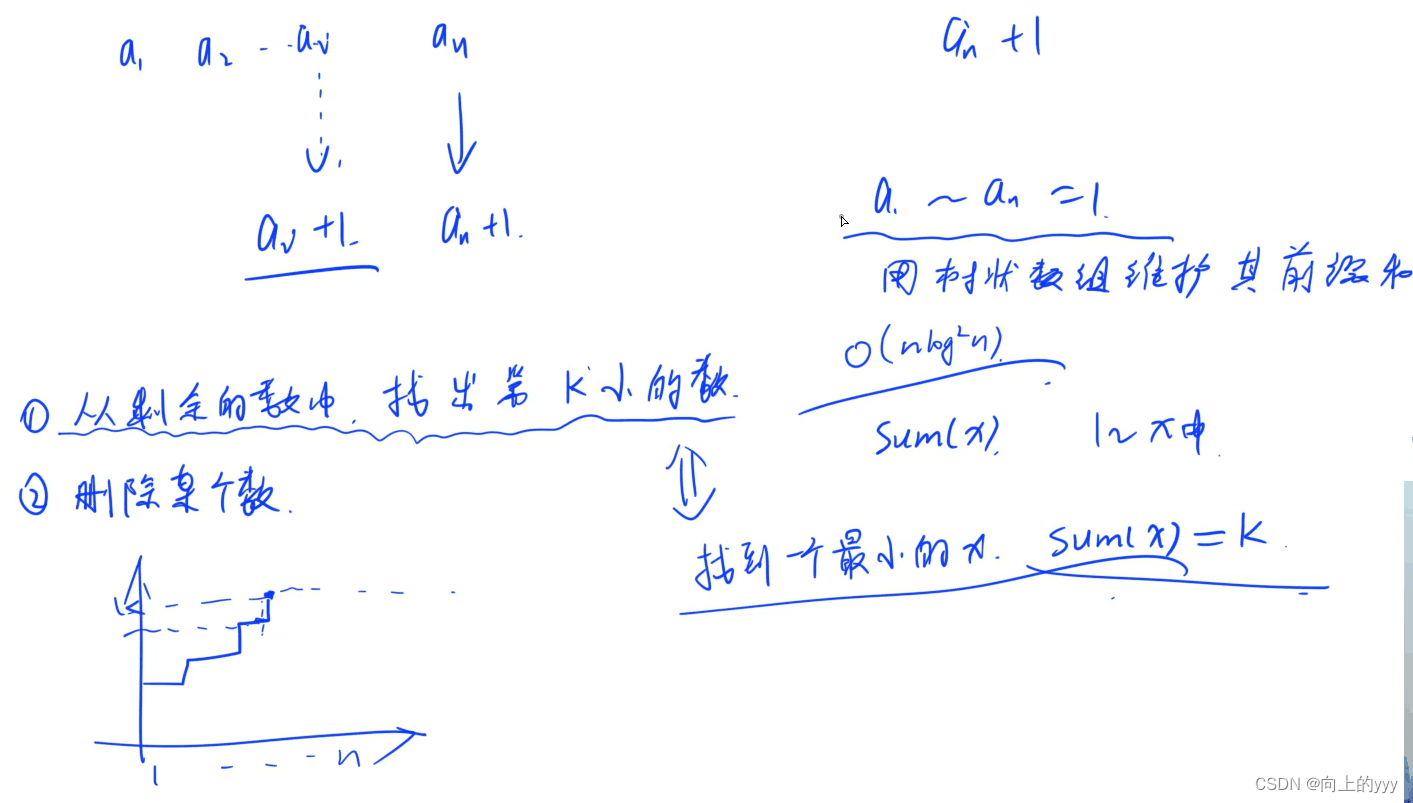
1. 通过样例分析，不能直接确定第一个位置的牛多高，但是可以确定最后一个位置的牛是多高，a[n]=0，k=a[n]+1，说明前面有0头牛比他低，那么最后一头牛的高度就是第k小的数（1~n中未被使用的顺序）；
2. 所以可以使用树状数组维护01序列的前缀和，便于查询k所在位置；从剩余的数中找第k小的数，可以转化为前缀和sum(x)=k这个条件，那么就转化为二分去查找这个满足条件的sum(x)；从[1,n]二分x（x就是mid），找到满足条件的x保存在t，然后存进方案ans；记得单点修改t处的值，减1变成0即可；
3. 在确定牛的身高，是倒着去确定的；并且记得初始化树状数组，因为维护的是01序列，且每个数均为被使用，可以直接初始化为1，而且此题的x也是表示位置，树状数组维护的都是前缀和，所以x一般都是索引；
   

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 100010;

int n;
int a[N];
int tr[N];//维护01序列的前缀和，便于查询k所在位置
int ans[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int c) {
    for (int i = x; i <= n; i += lowbit(i)) {
        tr[i] += c;
    }
}

//区间[1,x]的01序列和
int sum(int x) {
    int res = 0;
    for (int i = x; i; i -= lowbit(i)) {
        res += tr[i];
    }
    return res;
}

int main() {
    cin >> n;
    for (int i = 2; i <= n; ++i) {
        cin >> a[i];
    }
    for (int i = 1; i <= n; ++i) {
        //初始化刚开始 1~n的数都没用过，都是1
        add(i, 1);
    }
    //倒着去确定
    for (int i = n; i; --i) {
        //找没用过的数中，第k小的数
        int k = a[i] + 1;
        int l = 1, r = n;
        int t;//第k小的数所在位置
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if (sum(mid) >= k) {
                t = mid;
                r = mid - 1;
            } else {
                l = mid + 1;
            }
        }
        ans[i] = t;
        //第t个位置的数-1，变成了0，代表已用过
        add(t, -1);
    }
    for (int i = 1; i <= n; ++i) {
        cout << ans[i] << endl;
    }
    return 0;
}