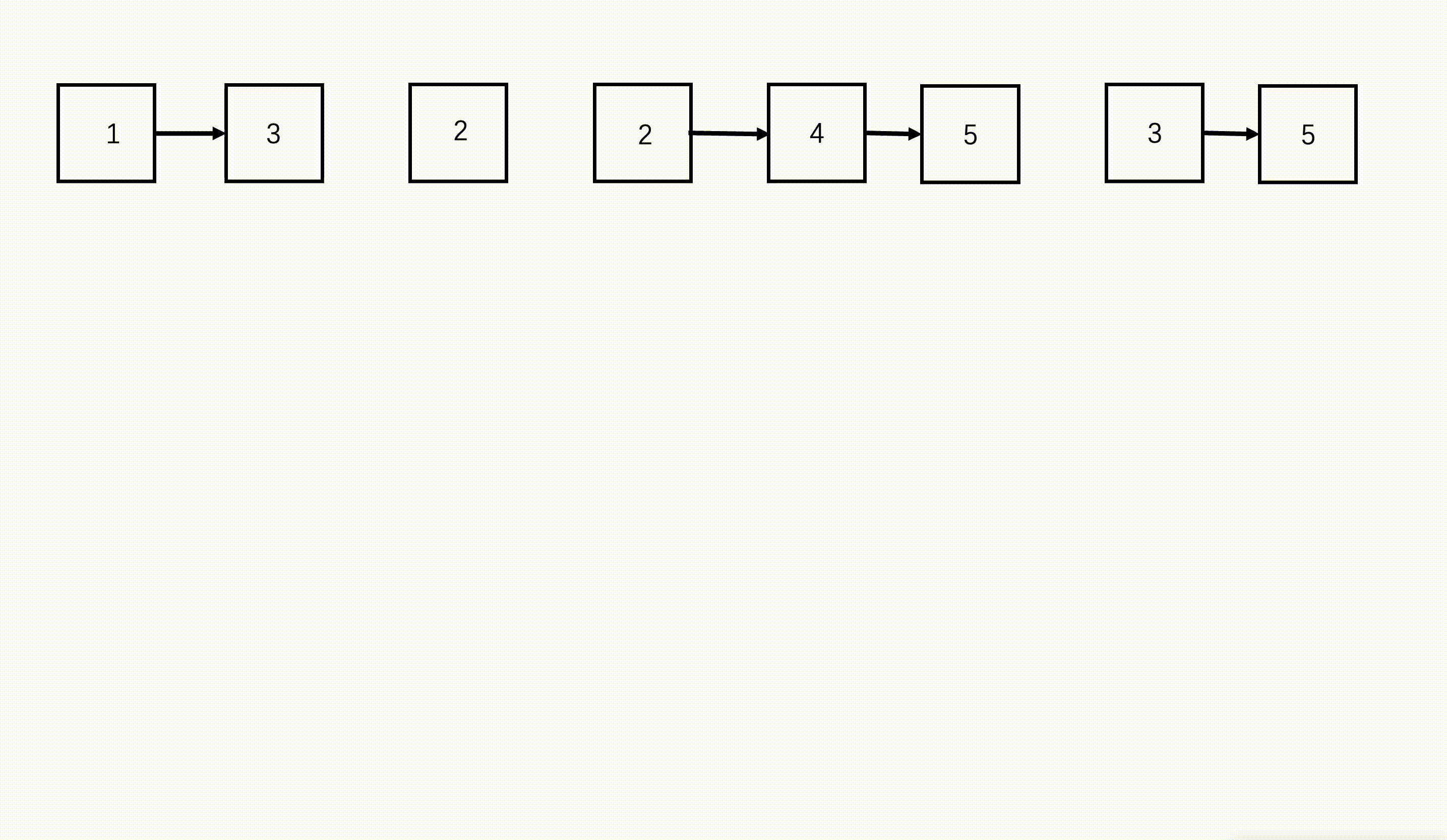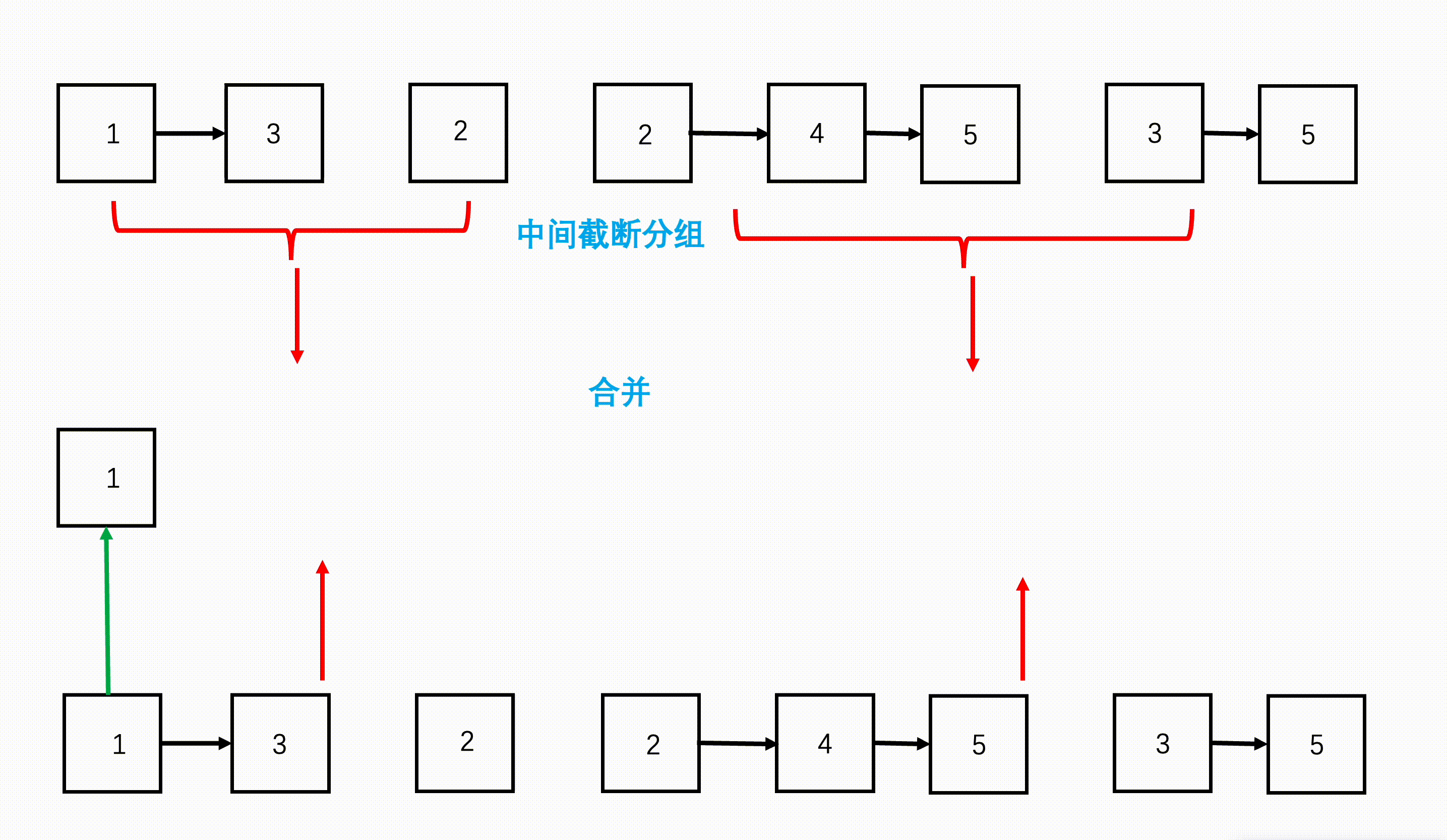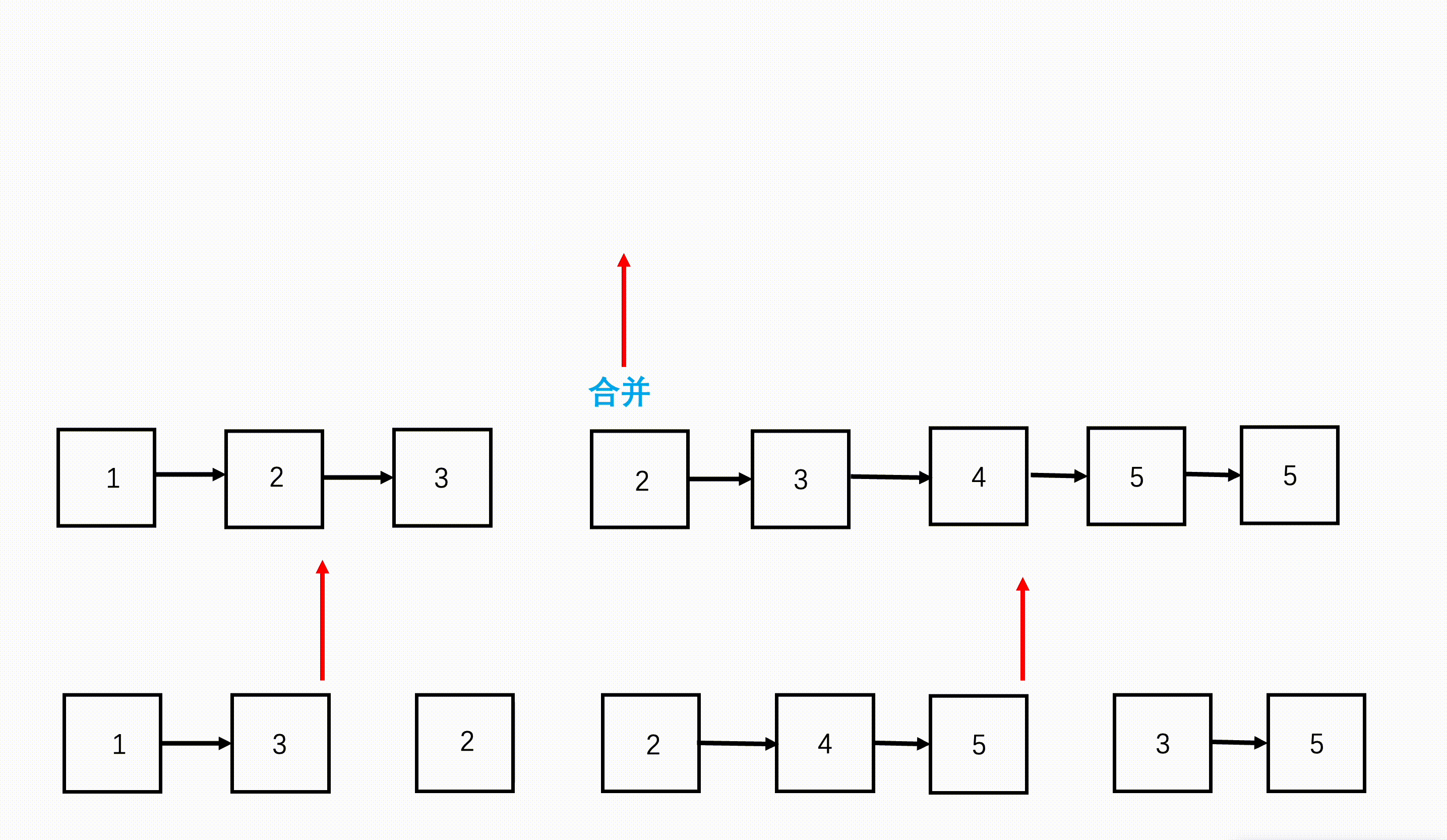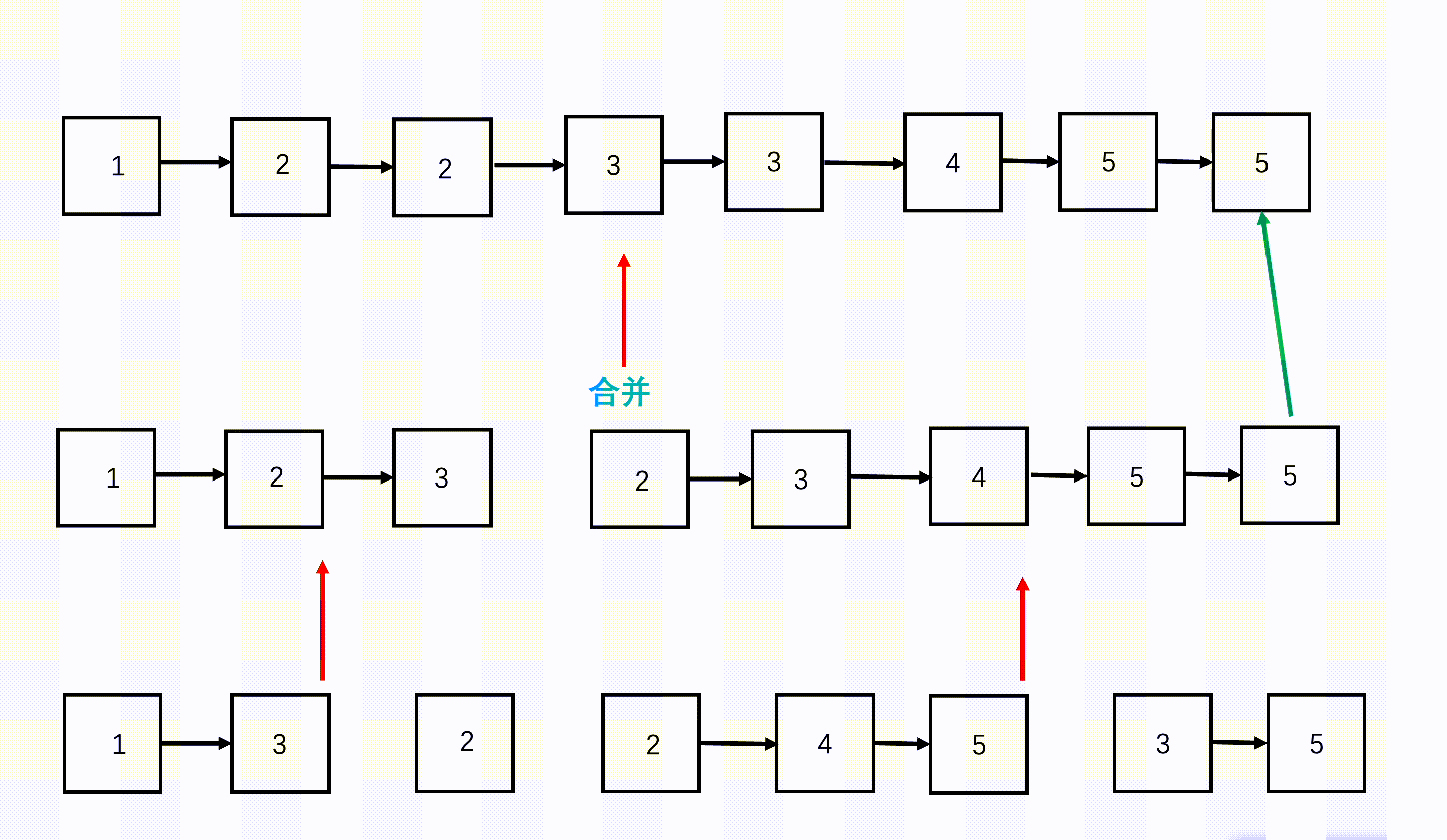1. 二极管
1.1 什么是二极管

二极管是一种电子元件,它的主要特点是只允许电流在一个方向通过,而另一个方向电流将被阻止。
下面是二极管的示意图:
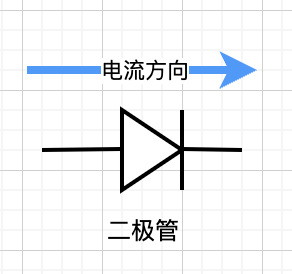
- 电流往箭头指向的地方流
1.2 二极管的作用
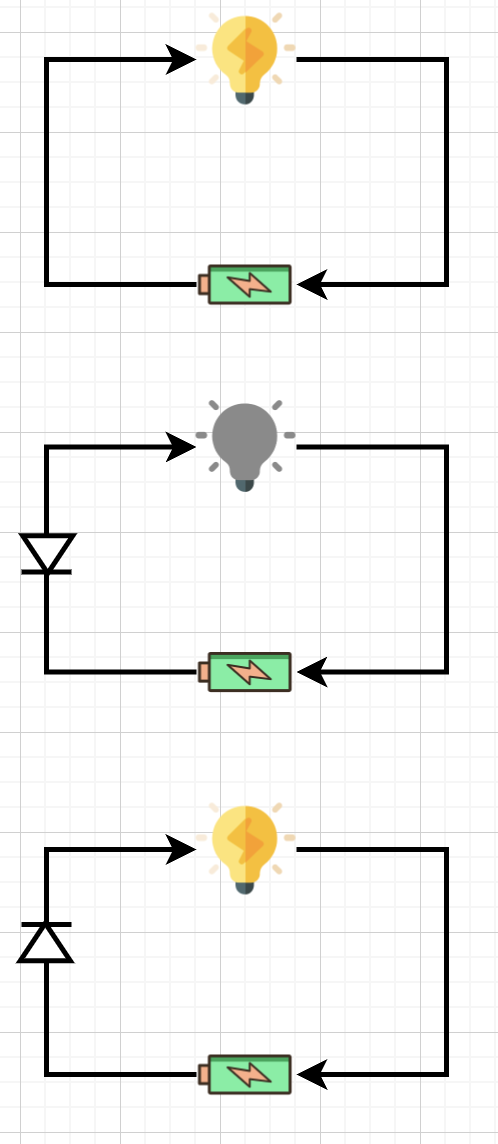
下面第一个图:给灯泡加上正负电压,电路上通过电流,灯泡会亮。(初中物理知识)。
第二个图:加上一个逆向的二极管,阻断了电流,电流流不过去,灯泡就不亮。
第三个图:加上一个顺向的二极管,电流照常流通,灯泡亮了。
可以通过水流来理解电路,水只能从高处往低处流,水流就是电流,高低差就是电压
2. 理解电路
2.1 小灯泡电路的简化
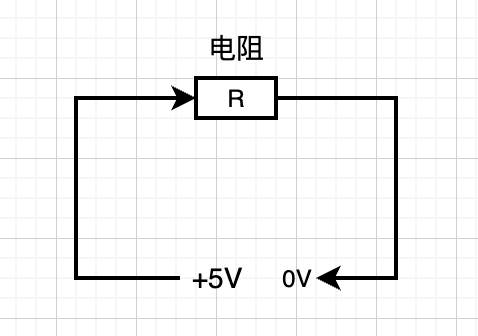
上述的灯泡的电路可以简化成如下所示,其中灯泡就是R电阻,生活中所有的电器设备都可以称之为电阻R。
2.2 生活中的电流

生活中我们通过插头就把设备连上电了,下面就是模拟把设备连接到电路中的示意图:
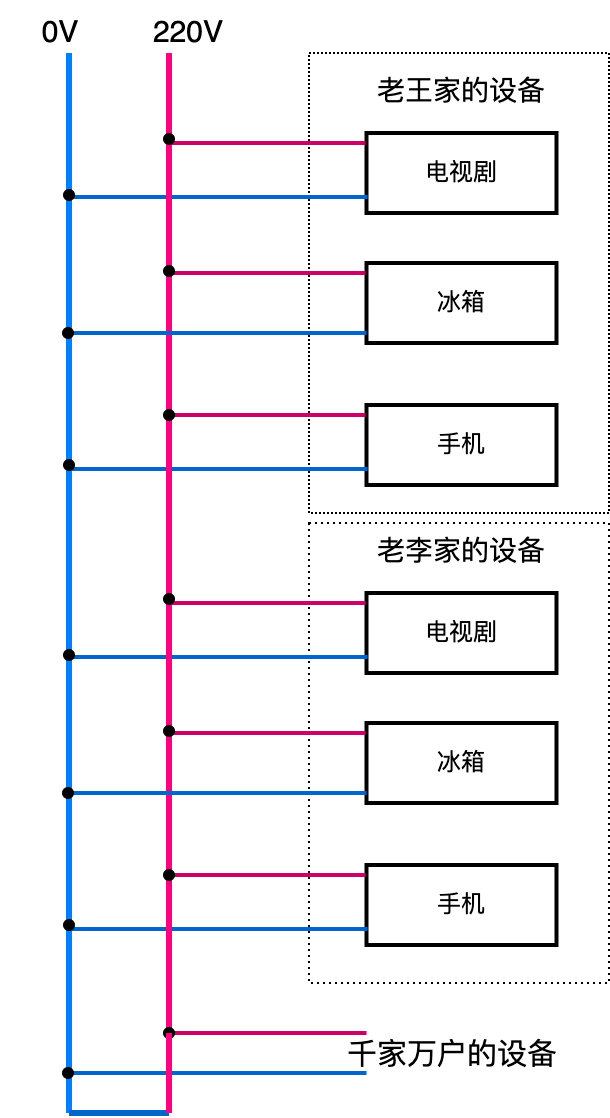
根据上图,是不是我们的插头一头要连接到220V上,一头要连接到0V上,但实际上我们插插头的时候随便插。
事实上生活中的用电跟上述还有点不一样,生活中用的是交流电,交流电的特点是电流会不断地在正向和负向之间变化,来回摆动。而直流电的电流方向始终保持一致不变,就像河流一样只朝一个方向流动。
交流电来回变化的频率是50Hz,意味着在每秒钟内,电流或电压的方向和大小会变化50次。
以水流来理解电流:水流从A处和B处之间来回流淌,1秒钟来回流通50次,当然水流速度很慢,但是电流的速度非常快,电流的速度就等于光的速度(30万公里每秒)。所以一趟1/50秒时间内可以有很多电流过。
3. 门
在电路中,门(Gate)是一种逻辑电路元件,用于执行逻辑操作和产生特定的输出信号。其中,与门(AND Gate)、或门(OR Gate)和非门(NOT Gate)是最基本和常见的三种门。
之前我们说过,二进制的0和1就对应集成电路中的高低电压,+5V和0V。
二级制数的操作变化就是通过一系列的包含输入输出的门来操作的。
3.1 与门
与门:当输入都为1时输出才为1,否则输出都是0。
输入是两个,输出是一个。
对应到物理中就是两个输入引脚都为+5V电压时,输出引脚才为+5V,否则输出都是0V。
| 输入 | 输入 | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |

- 从这也可以理解为什么叫门,就是电流这个门之后发生了变化。
与门的物理结构
当A和B都是+5V时,电源与A和B之间均无电压差,电路无电流,因而Y输出与电源同为高电平。这就是 “与电路”。
这里的二极管保证了电源的电流可以往A或B方向流,但A或B的电流无法流出去。
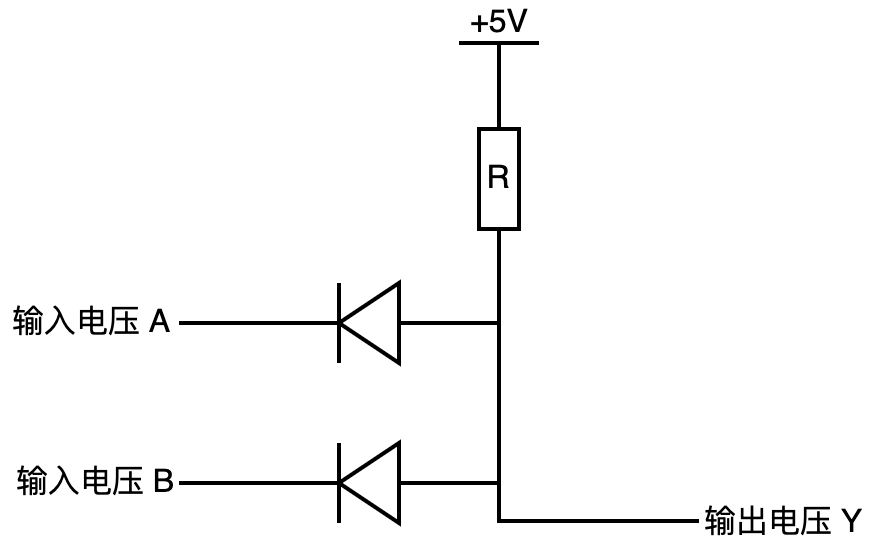
用水流和地势高低来理解:电源地势高5米,如果A和B地势都是5米,电源和A、B的地势一样高,则电源的水不会流向A和B,电源水会流向Y;如果A或B有一个地势为0米,则电源水会流向A或B,Y就没有水流过来。
3.2 或门
或门:当输入有一个为1时输出就为1。也就是说只有输入都为0时输出才为0,否则就为1。
| 输入 | 输入 | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
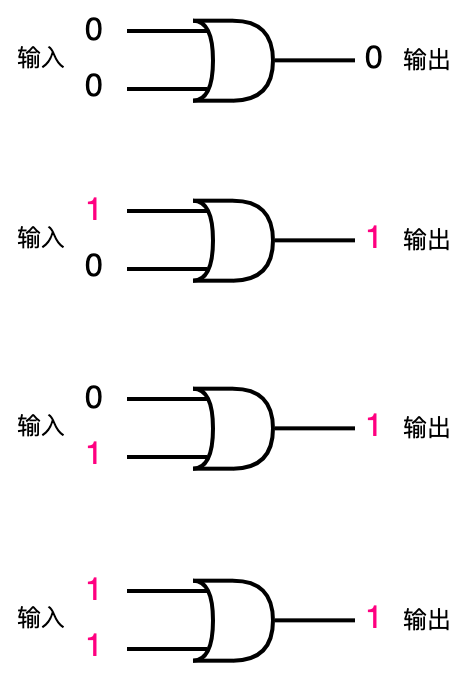
或门的物理结构
当A或B有一处有高电压,Y就会有高电压输出。
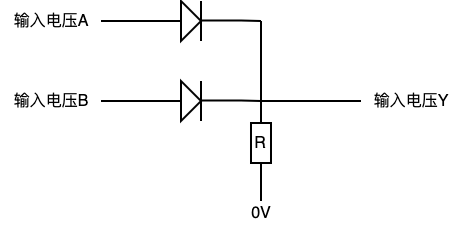
用水流和地势高低来理解:如果A或B有一个地势为5米,它的水就会流向Y。
3.3 非门
非门:当输入为1时输出就为0,当输入为0时输出就为1。就是相反。
非门就一个输入和一个输出。
| 输入 | 输出 |
|---|---|
| 0 | 1 |
| 1 | 0 |
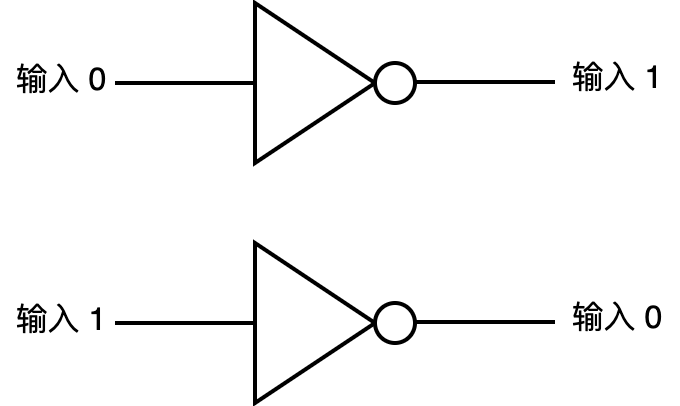
- 注意非门与二极管示意图有点像,注意区分!
3.4 异或门
异或门:输入一个0一个1时输出都为1,输入都是0或者都是1时输出都为0。
| 输入 | 输入 | 输出 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
- 两个不一样就为1
- 两个一样就为0
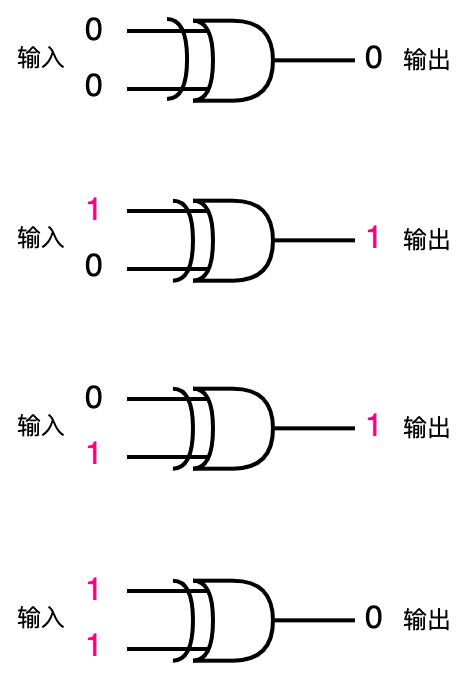
- 异或门在输入端比或门多出了一条曲线,除此之外它看上去和或门非常相像。
4. 二进制加法器
4.1 进位和加位
两个1位二进制数相加结果如下:
- 0加0等于0;
- 0加1等于1;
- 1加0等于1;
- 1加1等于0,进位为1
两个1位二进制数相加的结果可能是一个数位,也有可能是两个数位,我们这里都用两个数位来表示,不足两个的在开头补0,如下就是两个二进制数相加的结果:
| 输入 | 输入 | 相加结果 |
|---|---|---|
| 0 | 0 | 00 |
| 1 | 0 | 01 |
| 0 | 1 | 01 |
| 1 | 1 | 10 |
将相加的结果加位和进位两张表来存储。如下:
| 输入 | 输入 | 加位 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
| 输入 | 输入 | 进位 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
我们发现了什么规律,加位表就是异或操作的结果,进位表就是与操作的结果。
你发现了什么?
4.2 半加器
两个1位的二进制数相加就可以通过上面讲到的
异或门和与门这两个具体的电子元件来操作。
如下把一个异或门电子元件和一个与门电子元件连接在一起就可以生成一个用作1位二进制数相加的新的电子元件,我们称为半加器。
之所以叫半加器因为它只能算两个1位二进制数相加。

- 一个异或门和一个与门组成的半加器结果。
通常为了方便我们会将半加器画出如下示意图,简化内部结构。

- CO是进位输出 carry output的缩写。
4.3 全加器
如下是11001100和10101010两个数相加。我们按照低位在前高位在后排序成列表。
| 输入A | 输入B | 进位输入 | 加位输出 | 进位输出 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
- 低位的进位输出是高位的进位输入
- 两个8位二进制数相加,结果是9位二进制数,多了一个进位。
- 最后的结果是110010110。
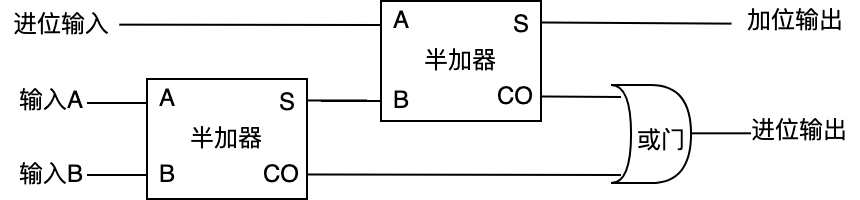
- 一个全加器需要两个
半加器和一个或门,而一个半加器需要一个异或门和一个与门,所以一个全加器需要2个异或门、2个与门、1个或门。
要理解它的工作原理,首先从最左边第一个半加器的输入A和输入B开始,其输出是一个加和及相应的进位。这个和必须与前一列的进位输入相加,然后再把它们输入到第二个半加器中。第二个半加器的输出和是最后的结果。两个半加器的进位输出又被输入到一个或门中。你可能会觉得,这里还需要一个半加法器,这当然是可行的。但是如果你了解了所有的可能性之后,你会发现,两个半加法器的进位输出是不会同时为1的。或门在这里已经足够,因为或门除了在输入都为1的时候以外,其他情况下结果和异或门结果相同。
为了避免重复地画上面的那个图,我们用以下形式来替代上图中的一堆符号,它称为全加器。
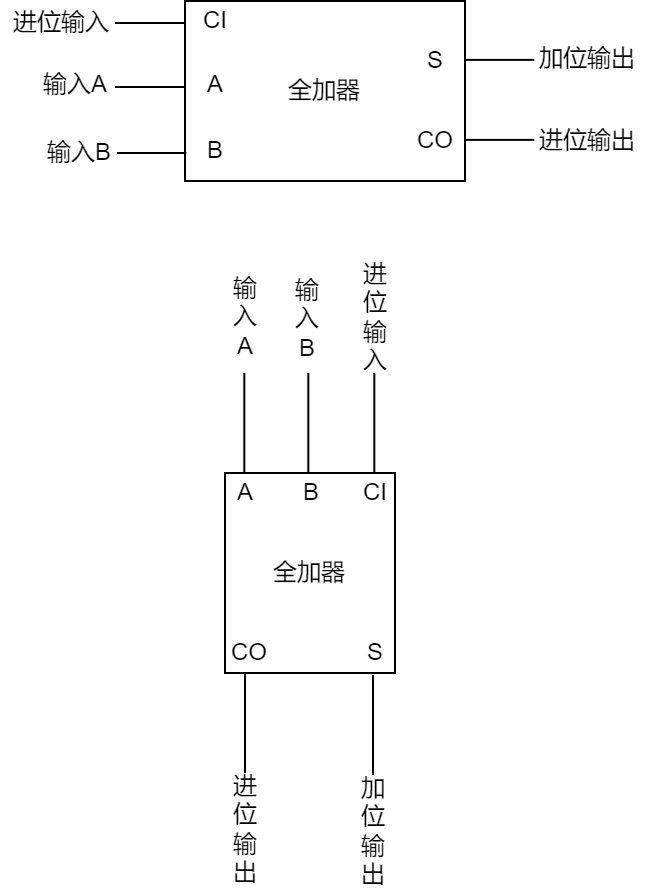
- CI是进位输入 carry input的缩写。
4.4 8位加法器
我们将8个全加器连接在一起就是一个8位加法器,它可以计算两个8位的二进制数相加了。它的输入是A0 ~ A7 、B0 ~ B7 、CI ,也就是两个8位的二进制数和一个进位输入。
它的输出是 S0 ~ S7、CO。
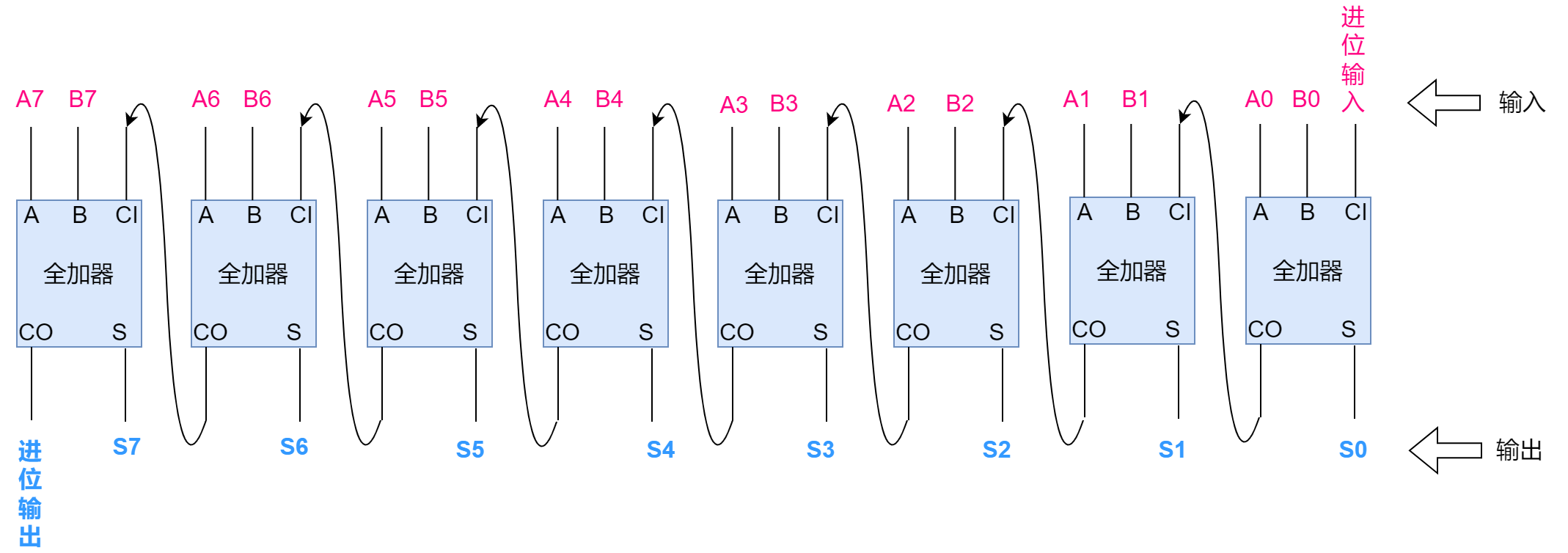
- 第1位的进位输出传递给第2位的进位输入,第2位的进位输出传递给第3位的进位输入,以此内推…
下面是是一个简化版的8位二进制加法器示意图。

如下:计算11001100和10101010这两个二进制数相加的结果等于110010110。
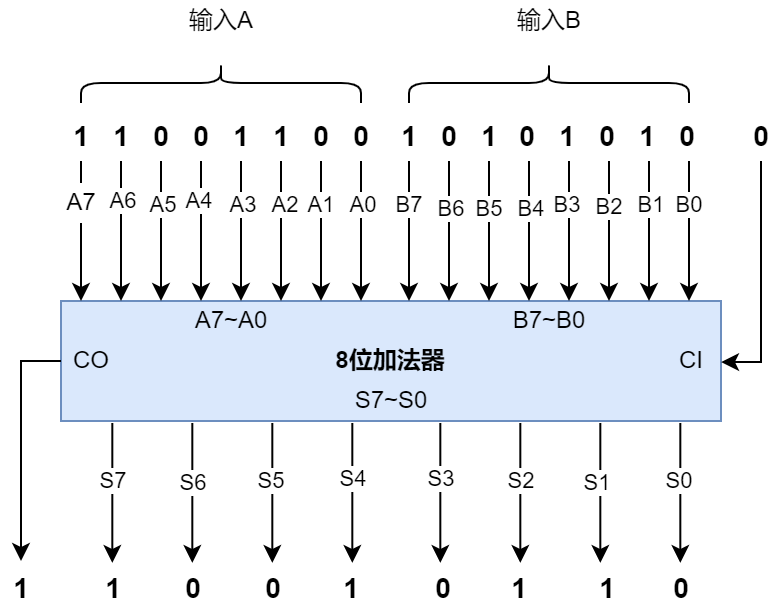
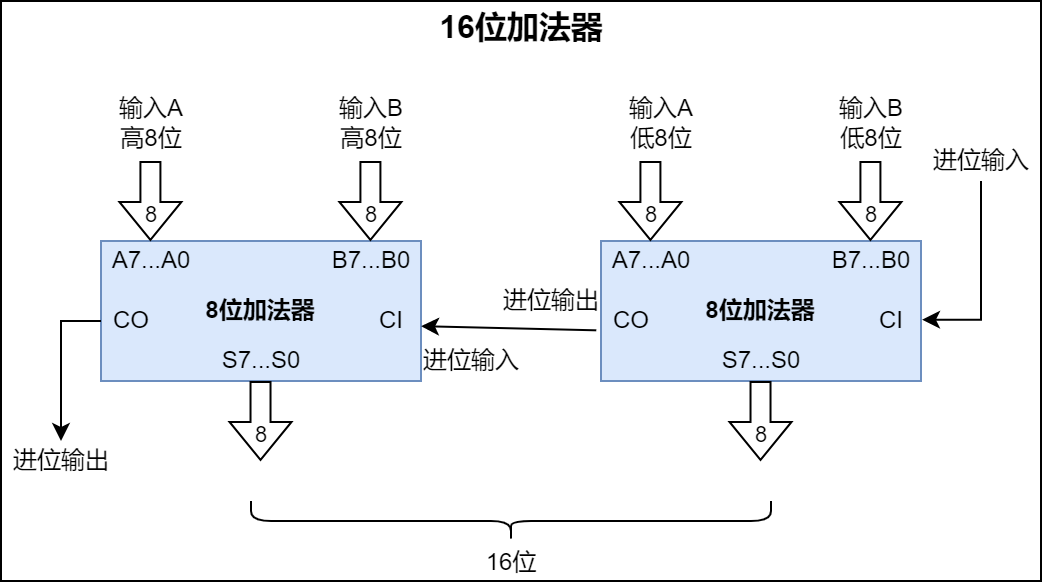
4.5 16位加法器
8位加法器的简化。
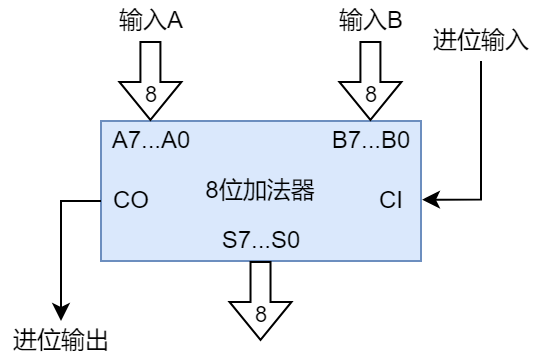
将两个8位加法器连在一起就是一个16位加法器。
5. 减法也是用加法
负数在计算机是以补数的形式来存储的。
负数的补数就是它对应的正数取反加1。
如-1,对应的正数是1,转化为二进制就是00000001,取反是11111110,加1就是11111111。
所以-1的补数就是11111111。
那么 1+(-1)假设在8位操作系统中: 00000001 + 11111111

- 因为操作系统是8位,只能存储8位,所以进位1省略掉。00000001 + 11111111 = 00000000
之所以能用补数表示负数,就是因为计算机的位数是有限制的。现在操作系统最多也就64位。
我们来计算一下 3+(-5)。
3的二进制是00000011
-5对应的正数是00000101,取反是11111010,加1是11111011。-5的补数就是11111011。

相加结果是11111110,结果开头是1,说明这是一个负数,是以补数的形式展示。
我们反推它对应的负数是多少,11111110减1是11111101,11111101取反是00000010,结果是2,对应的负数就是-2。
可以通过钟表来理解补数,因为钟表上只有12个小时。
比如现在是9点,我们需要调整到11点。可以往回拨10个小时,或者往前拨2个小时。都可以达到11点钟。

6. 结语
本篇讲了二极管、电路、与或非等逻辑门、二进制加法器等内容,内容很多而且较为难理解,请仔细阅读,不懂的地方请评论提问。
关注微信公众号:“小虎哥的技术博客”,让我们一起成为更优秀的程序员❤️!
文章和代码仓库:
gitee(推荐):https://gitee.com/cunzaizhe/xiaohuge-blog
github:https://github.com/tigerleeli/xiaohuge-blog