本文仅用于个人学习记录，使用的教材为汤家凤老师的《高等数学辅导讲义》。本文无任何盈利或者赚取个人声望的目的，如有侵权，请联系删除！

一、入门练习

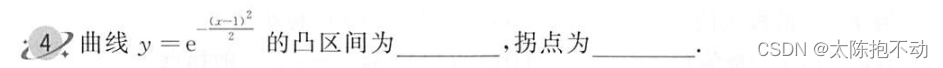
本题需要注意在写凸区间时应该是闭区间。

本题分子使用泰勒公式展开。

二、基础练习

本题先求了${\lim }_{a\to 0}$θ²的极限。

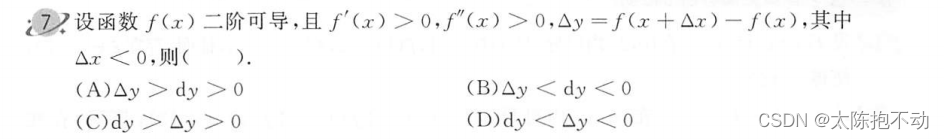
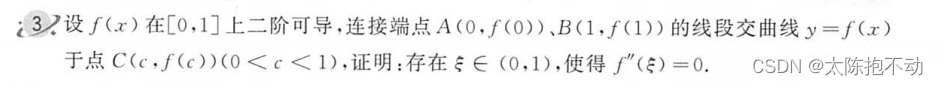
同一条线上的点斜率相同，也就是一阶导数值相等。

本题先假设有三个不同的根，然后使用罗尔定理证明存在矛盾。

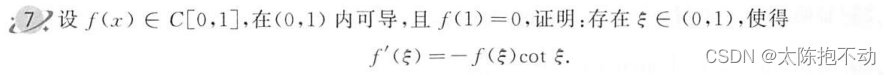
本题使用构造法，除此之外需要明确，cot x = $\frac{cosx}{sinx}$

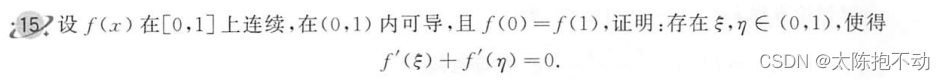
本题第三个点取区间中点。

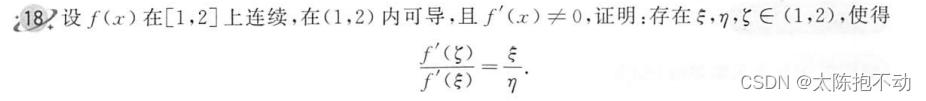
本题使用柯西中值定理，然后对柯西中值定理左半部分再使用拉格朗日中值定理，就会出现三个中值。

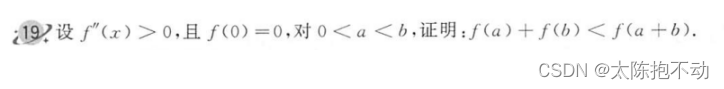
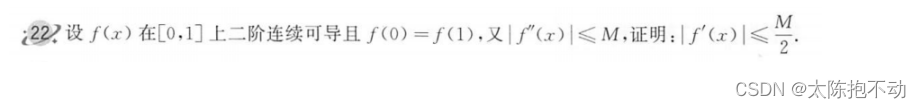
本题使用泰勒中值定理。

f(0) = f(x) + f’(x)(0 - x) + $\frac{f^{\prime \prime }(\xi )}{2!}$(0 - x)²，ξ ∈ (0,x)

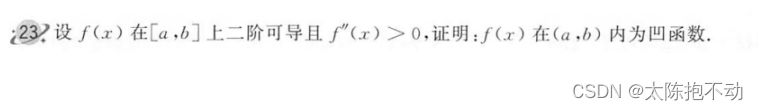
本题为判断凹凸性定理的证明。证明时使用了泰勒中值定理与凹凸性的定义。

本题需要根据二阶导数来判断一阶导数的单调性，再根据一阶导数来判断函数的单调性。

本体使用拉格朗日中值定理证明。

本题利用积分的可加性去绝对值，求出f(x)的表达式，然后求解。