0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

1 Theta*算法局限性

Theta*的运行瓶颈在于，每次扩展节点 $v$ 的邻节点 $w$ 时，都需要对 $\mathrm{parent}(v)$ 和 $w$ 进行一次Bresenham视线检测。然而，大部分邻节点最终不会被扩展，大量应用在视线检测上的计算资源被浪费。

在这里插入图片描述

Theta*的变种算法Lazy Theta*算法通过延迟评估技术提升Theta*的路径搜索速度。实验证明，在26邻域三维地图上，Lazy Theta*的视线检查数量比Theta*减少了一个数量级，且路径长度没有增加。

2 Lazy Theta*算法原理

Lazy Theta*在扩展节点 $v$ 的邻节点 $w$ 时，默认 $\mathrm{parent}(v)$ 和 $w$ 间存在视线，而无需对 $\mathrm{parent}(v)$ 和 $w$ 进行碰撞检测。当以节点 $w$ 为基础开始扩展时，才正式对它与父节点 $\mathrm{parent}(v)$ 计算视线。若视线存在，则无需更新信息(path2)；若视线不存在，则在邻域重新选择父节点(path1)。

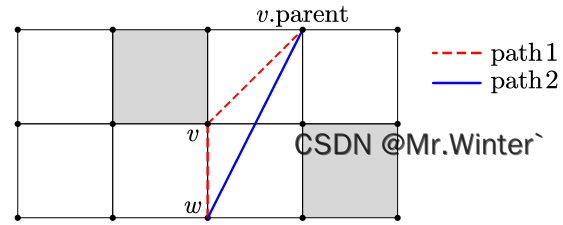
在这里插入图片描述
Lazy Theta*的算法流程如下所示。

在这里插入图片描述

3 Theta* VS. Lazy Theta*

Lazy Theta*牺牲了一定的路径优度，因为节点 $v$ 与其父节点间可能存在障碍，使节点 $v$ 的 $g$ 值往往小于真实值，导致从Open表中取出的优先节点可能并非最优的，所以Lazy Theta*的规划路径可能会更长。同时，当判定节点与其父节点间存在障碍后， $v$ 的父节点只能从邻域中更新，可能产生锯齿。Theta*与Lazy Theta*的对比实例如下

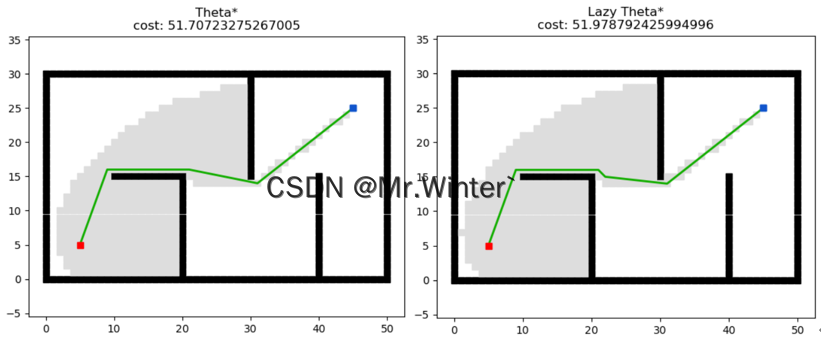
在这里插入图片描述

4 仿真实现

4.1 ROS C++实现

核心代码如下

bool LazyThetaStar::plan(const unsigned char* global_costmap, const Node& start, const Node& goal,
                         std::vector<Node>& path, std::vector<Node>& expand)
{
  // initialize
  costs_ = global_costmap;
  closed_list_.clear();
  path.clear();
  expand.clear();
  motion_ = getMotion();

  // push the start node into open list
  std::priority_queue<Node, std::vector<Node>, compare_cost> open_list;
  open_list.push(start);

  // main process
  while (!open_list.empty())
  {
    // pop current node from open list
    Node current = open_list.top();
    open_list.pop();

    _setVertex(current);

    if (current.g_ >= INFINITE_COST)
      continue;

    // current node does not exist in closed list
    if (closed_list_.find(current) != closed_list_.end())
      continue;

    closed_list_.insert(current);
    expand.push_back(current);

    // goal found
    if (current == goal)
    {
      path = _convertClosedListToPath(closed_list_, start, goal);
      return true;
    }

    // explore neighbor of current node
    for (const auto& m : motion_)
    {
      // explore a new node
      // path 1
      Node node_new = current + m;  // add the x_, y_, g_
      node_new.h_ = dist(node_new, goal);
      node_new.id_ = grid2Index(node_new.x_, node_new.y_);
      node_new.pid_ = current.id_;

      // current node do not exist in closed list
      if (closed_list_.find(node_new) != closed_list_.end())
        continue;

      // next node hit the boundary or obstacle
      if ((node_new.id_ < 0) || (node_new.id_ >= ns_) || (costs_[node_new.id_] >= lethal_cost_ * factor_))
        continue;

      // get parent node
      Node parent;
      parent.id_ = current.pid_;
      index2Grid(parent.id_, parent.x_, parent.y_);
      auto find_parent = closed_list_.find(parent);
      if (find_parent != closed_list_.end())
      {
        parent = *find_parent;
        // path 2
        _updateVertex(parent, node_new);
      }

      open_list.push(node_new);
    }
  }

  return false;
}

在这里插入图片描述

4.2 Python实现

核心代码如下

def plan(self):
	# OPEN set with priority and CLOSED set
	OPEN = []
	heapq.heappush(OPEN, self.start)
	CLOSED = []
	
	while OPEN:
	    node = heapq.heappop(OPEN)
	
	    # set vertex: path 1
	    try:
	        ...
	    except:
	        pass
	
	    # exists in CLOSED set
	    if node in CLOSED:
	        continue
	
	    # goal found
	    if node == self.goal:
	        CLOSED.append(node)
	        return self.extractPath(CLOSED), CLOSED
	
	    for node_n in self.getNeighbor(node):                
	        # exists in CLOSED set
	        if node_n in CLOSED:
	            continue
	        
	        # path1
	        node_n.parent = node.current
	        node_n.h = self.h(node_n, self.goal)
	
	        try:
	            p_index = CLOSED.index(Node(node.parent))
	            node_p = CLOSED[p_index]
	        except:
	            node_p = None
	
	        if node_p:
	            # path2
	            self.updateVertex(node_p, node_n)
	
	        # goal found
	        if node_n == self.goal:
	            heapq.heappush(OPEN, node_n)
	            break
	        
	        # update OPEN set
	        heapq.heappush(OPEN, node_n)
	    
	    CLOSED.append(node)
	return ([], []), []

4.3 Matlab实现

核心代码如下

while ~isempty(OPEN)
    % pop
    f = OPEN(:, 3) + OPEN(:, 4);
    [~, index] = min(f);
    cur_node = OPEN(index, :);
    OPEN(index, :) = [];
        
    % set vertex: path 1
    p_index = loc_list(cur_node(5: 6), CLOSED, [1, 2]);
    ...
    
    % exists in CLOSED set
    if loc_list(cur_node, CLOSED, [1, 2])
        continue
    end

    % update expand zone
    if ~loc_list(cur_node, EXPAND, [1, 2])
        EXPAND = [EXPAND; cur_node(1:2)];
    end

    % goal found
    if cur_node(1) == goal(1) && cur_node(2) == goal(2)
        CLOSED = [cur_node; CLOSED];
        goal_reached = true;
        cost = cur_node(3);
        break
    end
    if (cur_node(1) ==17) &&(cur_node(2) == 26)
        cur_node(1);
    end
    % explore neighbors
    for i = 1:motion_num
        % path 1
        node_n = [
            cur_node(1) + motion(i, 1), ...
            cur_node(2) + motion(i, 2), ...
            cur_node(3) + motion(i, 3), ...
            0, ...
            cur_node(1), cur_node(2)];
        node_n(4) = h(node_n(1:2), goal);

        % exists in CLOSED set
        if loc_list(node_n, CLOSED, [1, 2])
            continue
        end

        % obstacle
        if map(node_n(1), node_n(2)) == 2
            continue
        end

        p_index = loc_list(cur_node(5: 6), CLOSED, [1, 2]);
        if p_index
            node_p = CLOSED(p_index, :);
        else
            node_p = 0;
        end
        
        if node_p ~= 0
            node_n = update_vertex(node_p, node_n);
        end
        
        % update OPEN set
        OPEN = [OPEN; node_n];
    end
    CLOSED = [cur_node; CLOSED];
end