前言

当面对一个特征值极多的数据集时，使用PCA方法可以帮助降低数据的维度，从而减少特征值的数量。帮助我们更好的对数据进行分析。本文将介绍一下PCA算法。

在这里插入图片描述

一、原理

1.1. PCA介绍

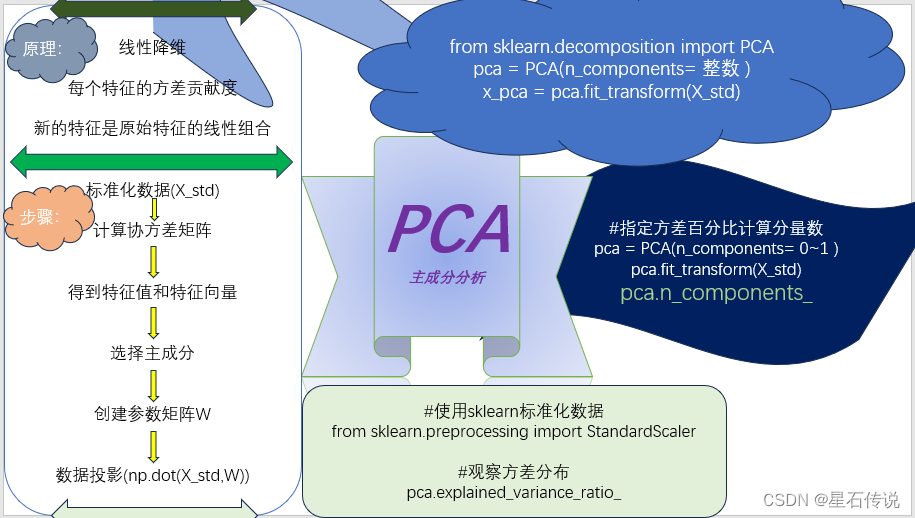
PCA（Principal Component Analysis），即主成分分析算法，又称主分量分析。一种常用的降维技术，用于将高维数据转换为低维表示，同时保留最重要的信息。

它通过线性变换将原始数据投影到一组新的正交特征向量上，这些特征向量称为主成分。

每个主成分都具有不同的方差，通常按照方差的大小进行排序，方差越大的主成分所包含的信息越多。

通过选择前k个主成分，可以实现数据的降维，保留数据集的对方差贡献最大的几个特征，尽可能保留原始数据的信息。

注意：
经过PCA降维后，得到的主成分是新的特征，不再是原有的特征。
PCA的目标是通过线性变换将原始数据投影到一个新的低维空间中，新的特征是原始特征的线性组合。

其实按我的理解，降维后得到的新特征就相当于原有特征经多项式线性回归后得到的结果，（也就是各个原有特征乘以它们对应的“权重系数”再相加得到的值）

1.2. 算法步骤

以下是PCA算法的详细步骤：

标准化数据：如果原始数据的各个特征具有不同的量纲，则需要对数据进行标准化处理，使得每个特征具有相同的量纲。（这是因为要计算协方差矩阵）
计算协方差矩阵：协方差矩阵反映了不同特征之间的相关性。通过计算标准化后的数据的协方差矩阵，可以得到特征之间的相关性信息。
计算特征值和特征向量：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。特征值表示每个主成分所包含的方差，特征向量表示主成分的方向。
选择主成分：按照特征值的大小进行排序，选择前k个特征值对应的特征向量作为主成分。
创建参数矩阵：将选定的主成分（特征向量）组成一个参数矩阵。
数据投影：将标准化后的数据乘以参数矩阵，得到降维后的数据。

二、代码实现

2.1. 基于numpy实现

#加载iris数据集
import numpy as np
import pandas as pd
from sklearn.datasets import load_iris
iris = load_iris()
data = iris["data"]
target = iris["target"]
df = pd.DataFrame(data=np.c_[iris["data"],iris["target"]],columns=list(iris["feature_names"] + ["target"]))
X = df.copy()
Y = X.pop("target")


#数据标准化
X_std = (X - np.mean(X, axis=0)) / np.std(X, axis=0)

# 计算变量之间的协方差矩阵（故要转置矩阵）
cov = np.cov(X_std.T)

#计算特征值和特征向量
eig_vals, eig_vecs = np.linalg.eig(cov)

#通过特征值对特征向量排序
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:, i]) for i in range(len(eig_vals))]
eig_pairs.sort(reverse=True)

#假设主成分的数量为2，则参数矩阵W：
W = np.hstack((eig_pairs[0][1].reshape(4,1),
               eig_pairs[1][1].reshape(4,1)))
               
print(W)
[[ 0.52106591 -0.37741762]
 [-0.26934744 -0.92329566]
 [ 0.5804131  -0.02449161]
 [ 0.56485654 -0.06694199]]

    
#将X_std与W相乘，得到降维后的x_pca
x_pca = np.dot(X_std,W)

#组合降维结果和标签数据
df_pca = pd.DataFrame(
    data=x_pca,
    columns= ["pca1","pca2"]
)
df_pca["target"] = Y
#print(df_pca)

2.2. 使用sklearn实现

import numpy as np
import pandas as pd
#使用sklearn标准化数据
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
X_std = std.fit_transform(X)

#使用sklearn的pca算法
from sklearn.decomposition import PCA
pca = PCA(n_components= 2) #n_components 表示降维后的特征数（即主成分数）
x_pca = pca.fit_transform(X_std)

df_pca = pd.DataFrame(
    data=x_pca,
    columns= ["pca1","pca2"]
)
df_pca["target"] = Y

2.3. 观察方差分布

##观察方差分布
results = pd.DataFrame(
    {"variance_ratio": pca.explained_variance_ratio_}
)
results["cumulative"] = results["variance_ratio"].cumsum()    #如在这个示例中，这2个成分的方差总占比（累积比率）为0.958132 
results["component"] = results.index +1
print(results)
   variance_ratio  cumulative  component
0        0.729624    0.729624          1
1        0.228508    0.958132          2

#查看原始特征的线性组合
print(pca.components_)
[[ 0.52106591 -0.26934744  0.5804131   0.56485654]
 [ 0.37741762  0.92329566  0.02449161  0.06694199]]

2.4. 指定方差百分比求分量数

#指定方差百分比计算分量数
pca = PCA(n_components= 0.90)
data_pca = pca.fit_transform(X_std)
print(pca.n_components_) #查看所需分量数
2
#由此可知要满足方差比率为0.90，最少要有2个主成分

另外，对于PCA() 函数中的 n_components参数，当 0 < n_components < 1 ，为小数时是填写所要求的方差比率；当为整数时，才是指定降维后的特征数。

三、优，缺点

3.1. 优点

PCA算法在降低数据维度、保留数据信息、去除冗余信息等方面有很好的效果

3.2. 缺点

数据线性相关性：PCA假设数据是线性相关的，对于非线性相关的数据，PCA的效果可能不理想。在处理非线性数据时，可以考虑使用其他非线性降维方法，如核主成分分析等。
特征解释性：降维后的特征是原始特征的线性组合，可能难以解释。因为降维后的特征往往没有直接的物理或业务含义。
数据标准化：PCA对数据的尺度敏感，需要对数据进行标准化处理，以确保各个特征具有相同的重要性。