“既然目前物理化学关于物质世界的最高理论成果,即所谓由量子力学和统计力学组成的第一原理,只能求算物质无生命的性质,而药物设计关心的却是有生命的性质.那么是否第一原理对药物设计就无所作为呢?不是的.也就是说,尽管目前的科学水平还未能对药物的治疗过程建立普遍有效的物理模型,那么还可以退而从数学模型着手作药物设计。
20世纪60年代,Hansch、藤田等开创了“经典QSAR”(定量结构活性关系,又称定量构效关系,quantitative structure-activity relationship)的研究.大量的研究结果说明:化合物的某种有生命性质(如毒性、半致死剂量LD50、活性等)与该化合物的某n种无生命性质pj有关,Φ=∫(p1,p2,---,Pn)尽管还无法找到这个普遍适用的函数关系f(或许它根本不存在).“经典QSAR”学科毕竟开辟了通过统计数学研究药物的道路,使得人们可以从无生命的物理化学性质构筑数学模型,预测有生命的性质.“设计”不再是思辨的、无法言传的,浮现出它理性的一面。
直到1964年,关于Free-Wilson方法和Hansch方法的两篇文章发表后,定量构效关系研究方法才进入了一个实际可行的发展期.用单个分子的物理、化学性质,即无生命性质,来描述其生物活性.不过这些用做自变量的无生命性质本质上都是分子的整体性质(bulk properties),不是分子某个几何位置处表现的性质.所以这时的QSAR方法不是直接与分子结构联系起来的.
从已知化合物的活性和各项已知的分子性质出发,采用多元线性回归分析等数据处理方法求得上述回归方程的各项系数.该过程称为学习部分.学习之后的统计模型称为活性模型.然后,如果某种化合物虽然其活性未知,但是它的分子性质却是已知的,或是可以计算得到的,那么就可以将已知的分子性质代入该活性模型,求得该化合物的活性.这称为预测部分.不断改变未知活性的化合物结构,通过其他方法求得它们的分子性质,继而用活性模型预测其活性,这样就可以不断提高它们的活性,达到“设计”新药物的目的.“学习+预测”就是QSAR方法的实质.”
《计算化学 - 从理论到分子模拟》 陈敏伯
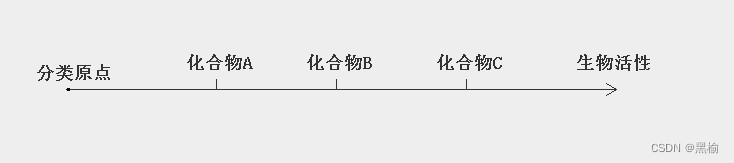
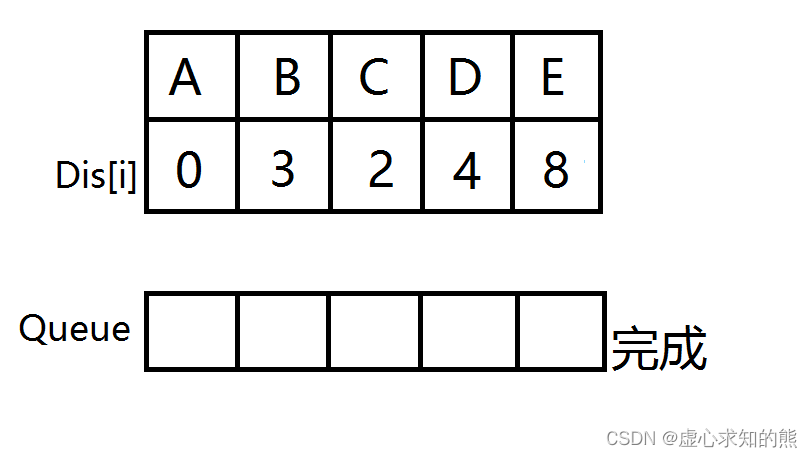
生命活性是由分子的结构决定的,按照某一生命活性比如溶血性的强弱把分子排序,比如化合物A<化合物B<化合物C。则得到了一条溶血性数轴。把所谓的化合物,理解为表达了一种结构,因此这就是关于结构的溶血能力的数轴,而所谓的结构当然也就是形态,因此这条溶血性数轴就是一条形态数轴。
| 分类原点\分类对象 | 5 | 7 | 2 | 4 | 3 | 9 | 1 | 6 | 8 |
| 0 | 5403 | 7822 | 8358.6 | 11983 | 12572 | 13347 | 23558 | 25606 | 27905 |
| 7 | 4 | 5 | 6 | 9 | 2 | 8 | 0 | 3 | |
| 1 | 9568.9 | 9577.5 | 10138 | 10241 | 10721 | 11793 | 16861 | 23558 | 35671 |
| 5 | 8 | 0 | 6 | 1 | 7 | 9 | 4 | 3 | |
| 2 | 7100.6 | 7658 | 8358.6 | 9360.1 | 11793 | 12556 | 13772 | 19985 | 33390 |
| 6 | 5 | 0 | 4 | 8 | 7 | 9 | 2 | 1 | |
| 3 | 8136.3 | 11703 | 12572 | 15200 | 17016 | 17331 | 19920 | 33390 | 35671 |
| 5 | 8 | 7 | 6 | 1 | 0 | 3 | 9 | 2 | |
| 4 | 5689.3 | 6106.3 | 7572.7 | 9021 | 9577.5 | 11983 | 15200 | 18524 | 19985 |
| 6 | 0 | 4 | 8 | 9 | 2 | 7 | 1 | 3 | |
| 5 | 5362.6 | 5403 | 5689.3 | 6116.4 | 6794.7 | 7100.6 | 8617.2 | 10138 | 11703 |
| 5 | 3 | 8 | 7 | 4 | 9 | 2 | 1 | 0 | |
| 6 | 5362.6 | 8136.3 | 8626.7 | 8983.4 | 9021 | 9044.2 | 9360.1 | 10241 | 25606 |
| 8 | 4 | 0 | 5 | 6 | 1 | 2 | 3 | 9 | |
| 7 | 7073.4 | 7572.7 | 7822 | 8617.2 | 8983.4 | 9568.9 | 12556 | 17331 | 20211 |
| 4 | 5 | 9 | 7 | 2 | 6 | 1 | 3 | 0 | |
| 8 | 6106.3 | 6116.4 | 6966.3 | 7073.4 | 7658 | 8626.7 | 16861 | 17016 | 27905 |
| 5 | 8 | 6 | 1 | 0 | 2 | 4 | 3 | 7 | |
| 9 | 6794.7 | 6966.3 | 9044.2 | 10721 | 13347 | 13772 | 18524 | 19920 | 20211 |
按照前面的实验,形态没有内在的递进规律,两个形态在形态数轴上的位置完全取决于分类原点。
( 分类原点 , 分类对象 )---m*n*2---( 1, 0 )( 0, 1 )
比如用mnist的0,1,…,9作为分类原点,而把剩余的9个形态作为分类对象,用迭代次数作为距离,得到的10条形态数轴,上面的1,2的顺序和位置各不相同。在以0,3,5,6,8为分类原点的数轴上2在1的前面,而在分类原点为4,7,9的数轴上1在2 的前面。而且1与2的相对距离也各不相同。
| 分类原点\分类对象 | 5 | 7 | 2 | 4 | 3 | 9 | 1 | 6 | 8 |
| 0 | 5403 | 7822 | 8358.6 | 11983 | 12572 | 13347 | 23558 | 25606 | 27905 |
假设现在已知一条溶血性数轴上有两个化合物1和2,并且1的溶血性要大于2,二者的强度比为23558/8358.完全有可能由这个强度比和1与2的形态,反向的构造出分类原点,这时所谓的分类原点就是一种等效的药效团。也就是认为这种溶血性是由不同的结构与这个药效团这两个形态相互作用导致。
已知分类原点就完全可以用一种类似gan的方法找到其他的分子结构,进一步的完善这条溶血性数轴,并发现更有效的药物。





![[2022-12-17]神经网络与深度学习第5章 - 循环神经网络(part 1)](https://img-blog.csdnimg.cn/50a2576319ce444ca3dbf777500e7a2f.png#pic_center)
![[机器人学习]-树莓派6R机械臂运动学分析](https://img-blog.csdnimg.cn/ab23a9b9c6e646bfa5d182dc7a6c4622.png)