contents
- 循环神经网络 part 1 - RNN记忆能力实验
- 写在开头
- 循环神经网络的记忆能力实验
- 数据集构建
- 数据集构建函数
- 数据集加载
- 构建 Dataset类
- 模型构建
- 嵌入层
- SRN层
- 自己实现
- torch框架实现
- 比较
- 线性层
- 模型汇总
- 模型训练
- 训练指定长度的数字预测模型
- 模型评价
- 写在最后
循环神经网络 part 1 - RNN记忆能力实验
写在开头
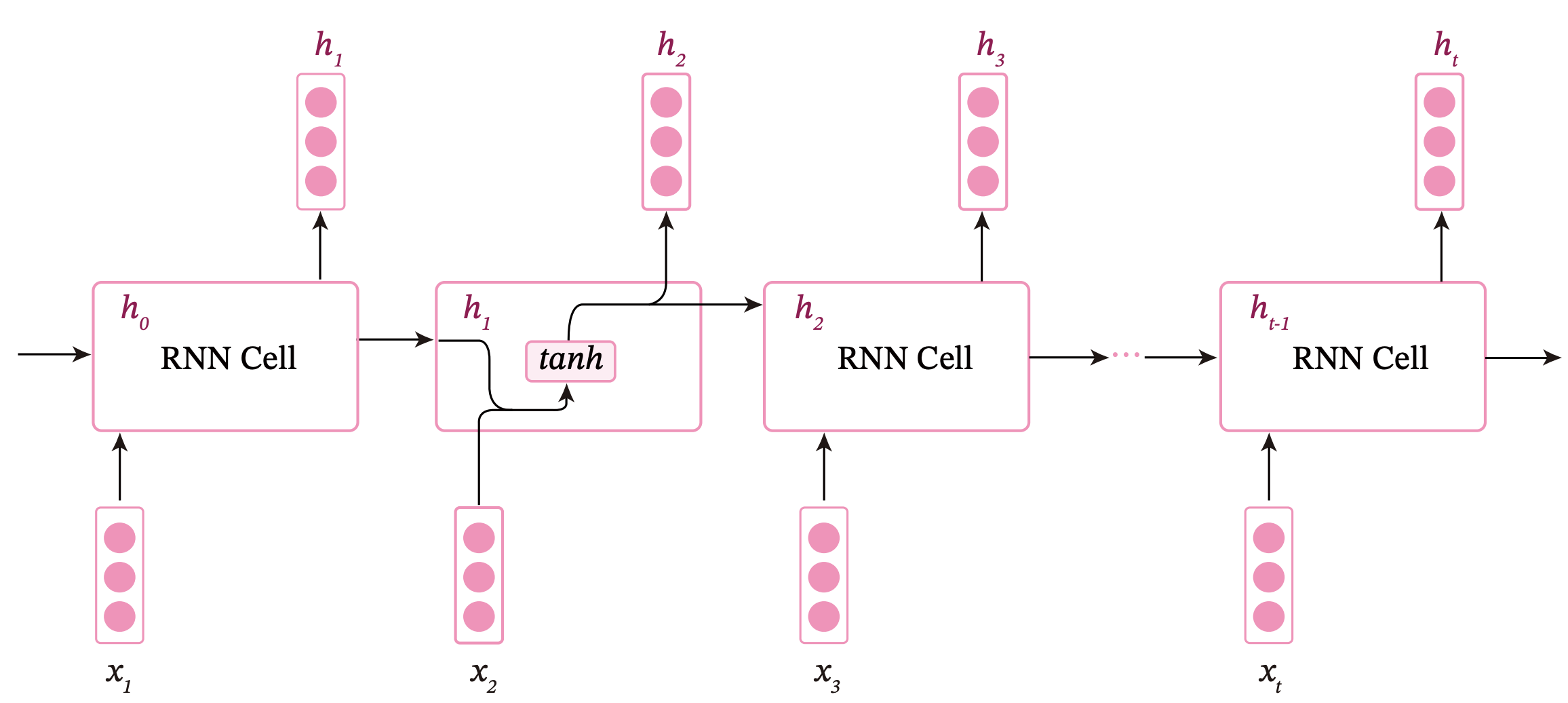
在前面的作业中我们就已经提及,循环神经网络是带有记忆能力的一类神经网络结构,就像数字电路中的时序逻辑电路——它的输出不仅取决于输入的值、也取决于前面时刻所输入的值。神经元不但可以接收其他神经元的信息,也可以接受自身的信息,形成具有环路的网络结构。这样的记忆功能,更与生物学上的神经元贴近,也在很多情况下有着更为优越的性能。目前,循环神经网络已经被广泛应用在语音识别、语言模型以及自然语言生成等众多任务之上。本实验进行研究和测试的是简单循环神经网络。
维基百科介绍如下:

查了一下,FNN多指有门控状态的反馈神经网络,尽管其也有前馈神经网络的意思,但是不常用。
循环神经网络的记忆能力实验
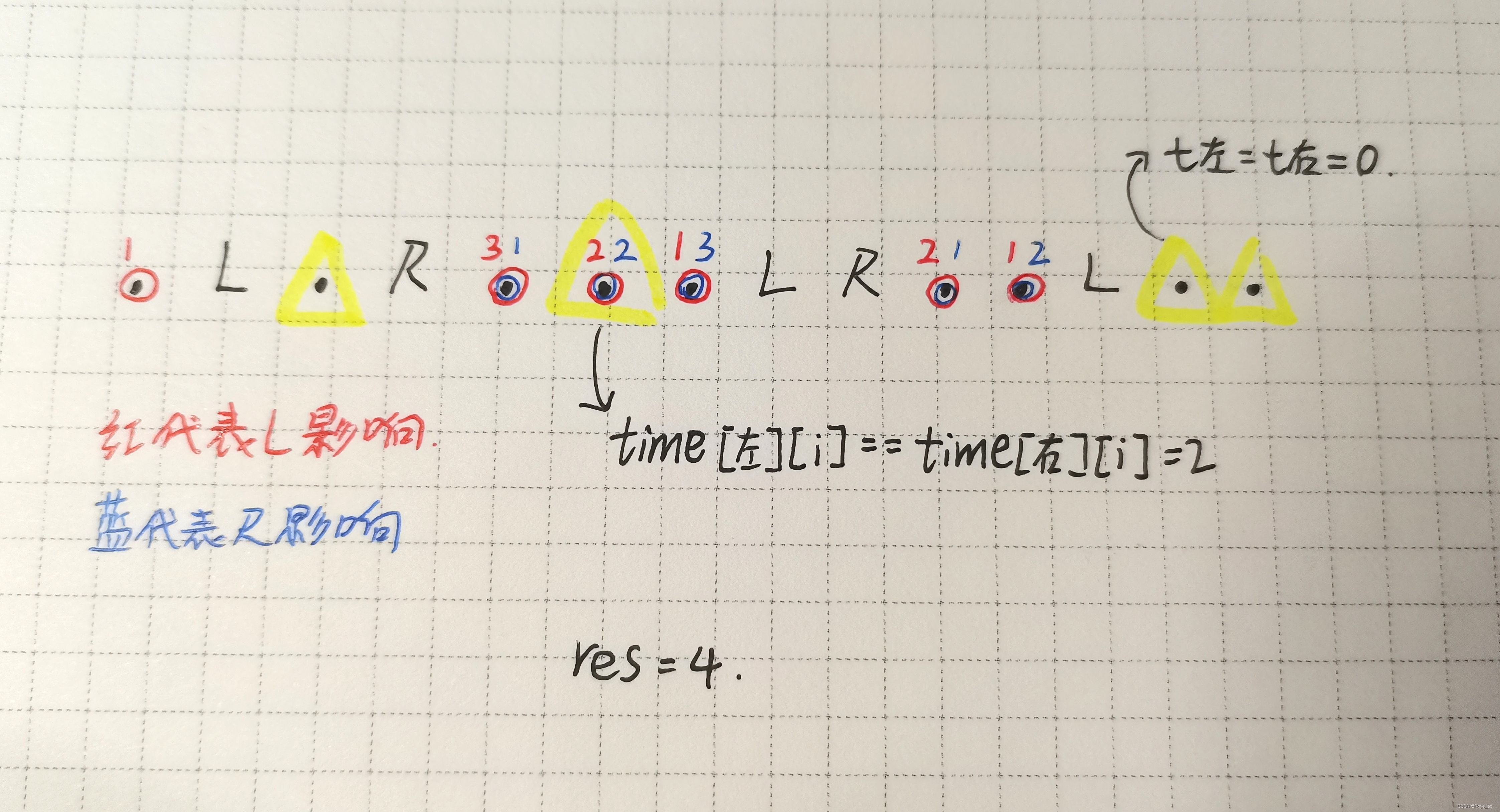
简单循环网络在参数学习时存在长程依赖问题,很难建模长时间间隔(Long Range)的状态之间的依赖关系。为了测试简单循环网络的记忆能力,本节构建一个数字求和任务进行实验。
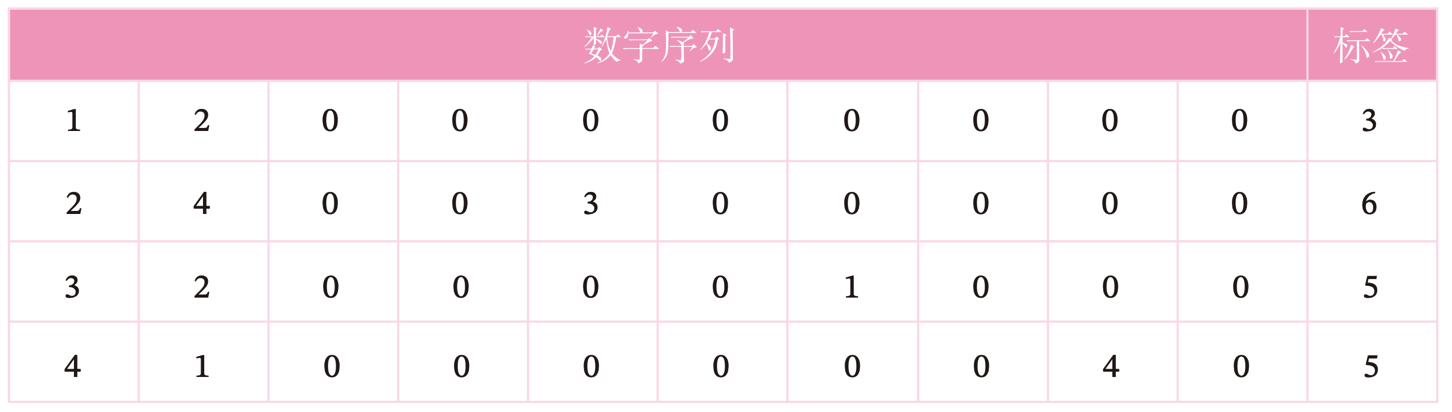
数字求和任务的输入是一串数字,前两个位置的数字为0-9,其余数字随机生成(主要为0),预测目标是输入序列中前两个数字的加和。如果序列长度越长,准确率越高,则说明网络的记忆能力越好。因此,我们可以构建不同长度的数据集,通过验证简单循环网络在不同长度的数据集上的表现,从而测试简单循环网络的长程依赖能力。数据集样例如下:
数据集构建
由于在本任务中,输入序列的前两位数字为 0 − 9,其组合数是固定的,所以可以穷举所有的前两位数字组合,并在后面默认用0填充到固定长度。 但考虑到数据的多样性,这里对生成的数字序列中的零位置进行随机采样,并将其随机替换成0-9的数字以增加样本的数量。
数据集构建函数
我们可以通过设置kk的数值来指定一条样本随机生成的数字序列数量。当生成某个指定长度的数据集时,会同时生成训练集、验证集和测试集。当k=3时,生成训练集。当k=1时,生成验证集和测试集。代码实现如下:
import random
import numpy as np
# 固定随机种子
random.seed(0)
np.random.seed(0)
def generate_data(length, k, save_path):
if length < 3:
raise ValueError("The length of data should be greater than 2.")
if k == 0:
raise ValueError("k should be greater than 0.")
# 生成100条长度为length的数字序列,除前两个字符外,序列其余数字暂用0填充
base_examples = []
for n1 in range(0, 10):
for n2 in range(0, 10):
seq = [n1, n2] + [0] * (length - 2)
label = n1 + n2
base_examples.append((seq, label))
examples = []
# 数据增强:对base_examples中的每条数据,默认生成k条数据,放入examples
for base_example in base_examples:
for _ in range(k):
# 随机生成替换的元素位置和元素
idx = np.random.randint(2, length)
val = np.random.randint(0, 10)
# 对序列中的对应零元素进行替换
seq = base_example[0].copy()
label = base_example[1]
seq[idx] = val
examples.append((seq, label))
# 保存增强后的数据
with open(save_path, "w", encoding="utf-8") as f:
for example in examples:
# 将数据转为字符串类型,方便保存
seq = [str(e) for e in example[0]]
label = str(example[1])
line = " ".join(seq) + "\t" + label + "\n"
f.write(line)
print(f"generate data to: {save_path}.")
# 定义生成的数字序列长度
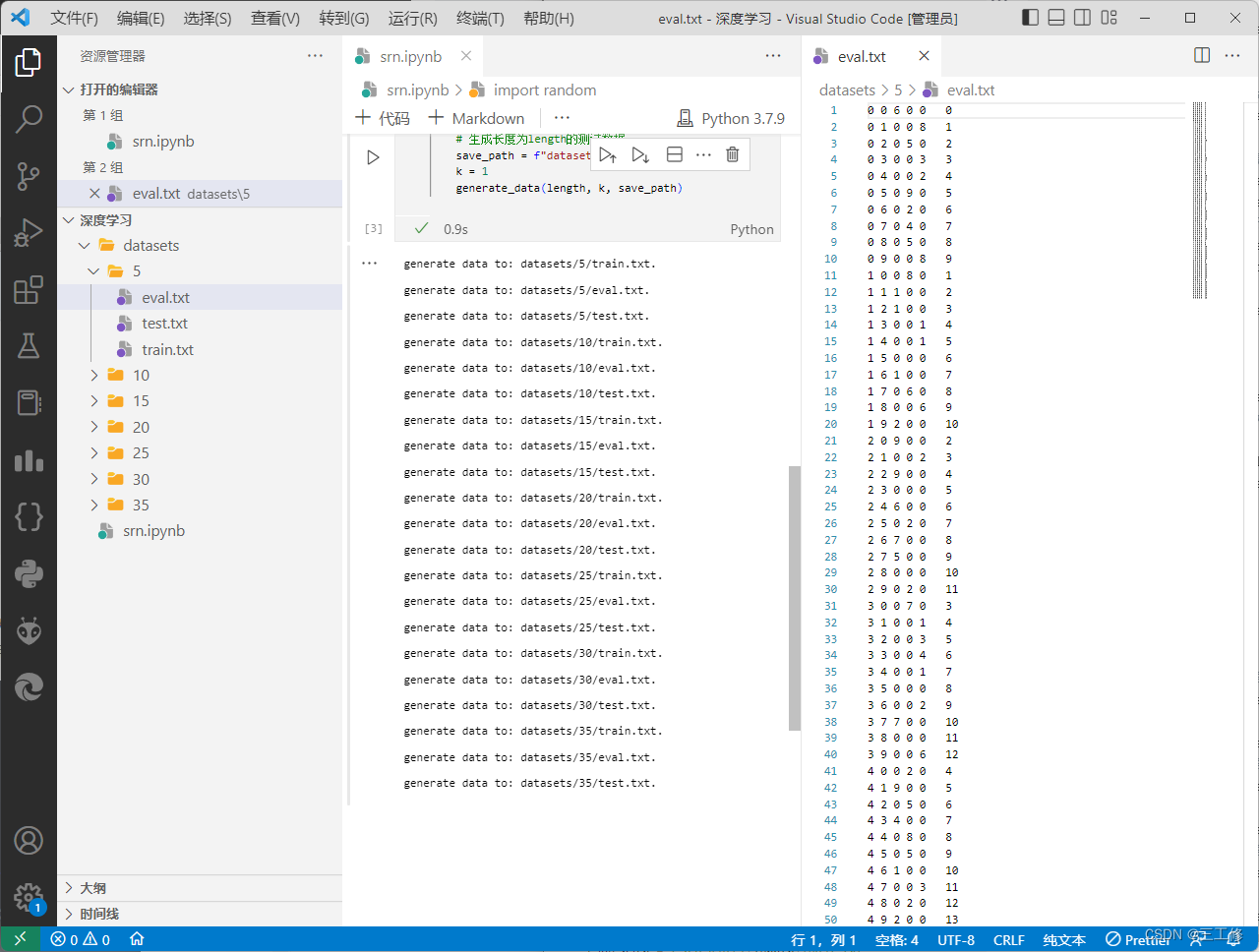
lengths = [5, 10, 15, 20, 25, 30, 35]
for length in lengths:
# 生成长度为length的训练数据
save_path = f"datasets/{length}/train.txt"
k = 3
generate_data(length, k, save_path)
# 生成长度为length的验证数据
save_path = f"datasets/{length}/eval.txt"
k = 1
generate_data(length, k, save_path)
# 生成长度为length的测试数据
save_path = f"datasets/{length}/test.txt"
k = 1
generate_data(length, k, save_path)
可见运行效果如下:
数据集加载
数据集加载的代码如下:
import os
# 加载数据
def load_data(data_path):
# 加载训练集
train_examples = []
train_path = os.path.join(data_path, "train.txt")
with open(train_path, "r", encoding="utf-8") as f:
for line in f.readlines():
# 解析一行数据,将其处理为数字序列seq和标签label
items = line.strip().split("\t")
seq = [int(i) for i in items[0].split(" ")]
label = int(items[1])
train_examples.append((seq, label))
# 加载验证集
eval_examples = []
eval_path = os.path.join(data_path, "eval.txt")
with open(eval_path, "r", encoding="utf-8") as f:
for line in f.readlines():
# 解析一行数据,将其处理为数字序列seq和标签label
items = line.strip().split("\t")
seq = [int(i) for i in items[0].split(" ")]
label = int(items[1])
eval_examples.append((seq, label))
# 加载测试集
test_examples = []
test_path = os.path.join(data_path, "test.txt")
with open(test_path, "r", encoding="utf-8") as f:
for line in f.readlines():
# 解析一行数据,将其处理为数字序列seq和标签label
items = line.strip().split("\t")
seq = [int(i) for i in items[0].split(" ")]
label = int(items[1])
test_examples.append((seq, label))
return train_examples, eval_examples, test_examples
# 设定加载的数据集的长度
length = 5
# 该长度的数据集的存放目录
data_path = f"datasets/{length}"
# 加载该数据集
train_examples, eval_examples, test_examples = load_data(data_path)
print("训练集数量:", len(train_examples))
print("验证集数量:", len(eval_examples))
print("测试集数量:", len(test_examples))
可以看到结果如下:

构建 Dataset类
为了方便数据集的加载和使用,我们继承torch的Dataset类进行数据集构建:
import torch
from torch.utils.data import Dataset
class DigitSumDataset(Dataset):
def __init__(self, data):
self.data = data
def __getitem__(self, idx):
example = self.data[idx]
seq = torch.tensor(example[0], dtype=torch.int64)
label = torch.tensor(example[1], dtype=torch.int64)
return seq, label
def __len__(self):
return len(self.data)
模型构建
简单的循环神经网络模型结构如下图所示:
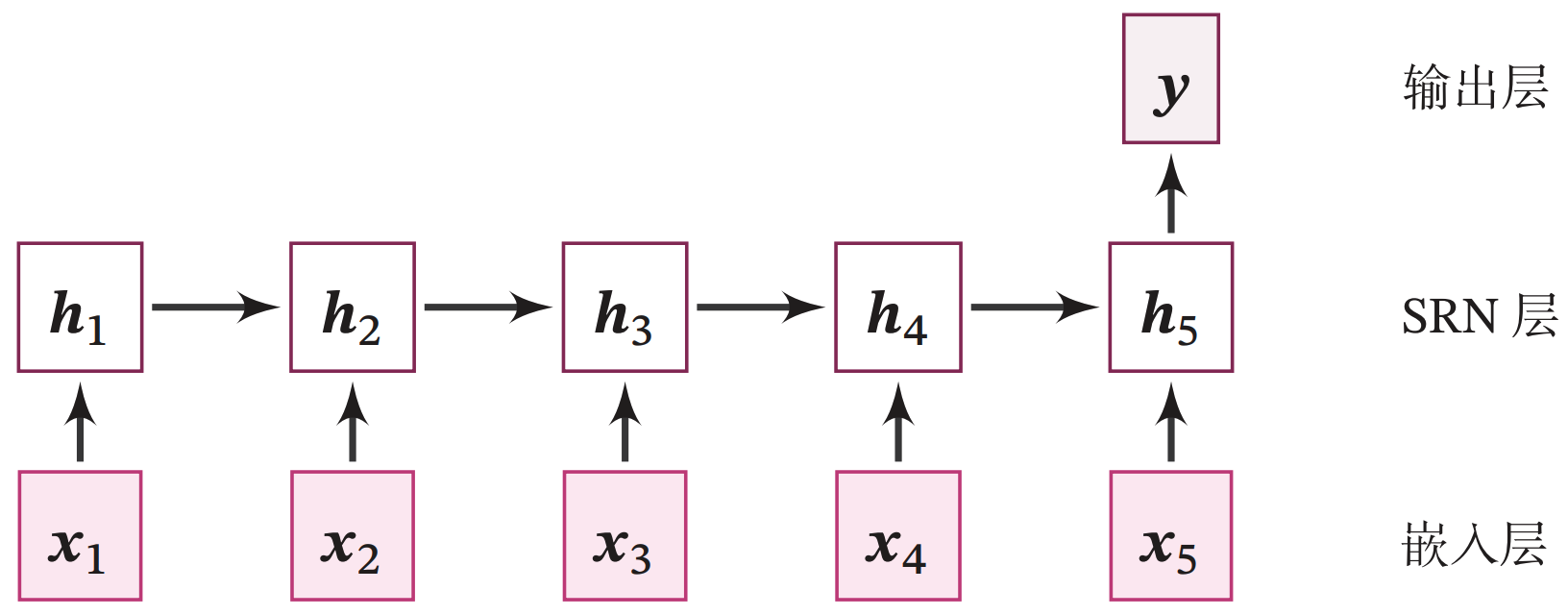
整个模型由以下几个部分组成:
(1) 嵌入层:将输入的数字序列进行向量化,即将每个数字映射为向量;
(2) SRN 层:接收向量序列,更新循环单元,将最后时刻的隐状态作为整个序列的表示;
(3) 输出层:一个线性层,输出分类的结果。
嵌入层
为了更好地表示数字,需要将数字映射为一个嵌入向量。嵌入向量中的每个维度均能用来刻画该数字本身的某种特性。由于向量能够表达该数字更多的信息,利用向量进行数字求和任务,可以使得模型具有更强的拟合能力。
首先我们构建一个嵌入矩阵
E
∈
R
10
×
M
E\in \mathbb{R}^{10\times M}
E∈R10×M,其中第i行对应数字i的嵌入向量,每个嵌入向量的维度是M。给定一个组数字序列
S
∈
R
B
×
L
S\in \mathbb{R}^{B\times L}
S∈RB×L,其中B为批大小,L为序列长度,可以通过查表将其映射为嵌入表示
X
∈
R
B
×
L
×
M
X\in \mathbb{R}^{B\times L\times M}
X∈RB×L×M。

或者也可以将每个数字表示为10维的独热编码向量,使用矩阵运算得到嵌入表示为:
X
=
S
′
E
X=S'E
X=S′E
其中
S
′
∈
R
B
×
L
×
10
S'\in \mathbb{R}^{B\times L \times 10}
S′∈RB×L×10。
由此可以得到嵌入层类的实现如下:
import torch.nn as nn
class Embedding(nn.Module):
def __init__(self, num_embeddings, embedding_dim):
super(Embedding, self).__init__()
W_attr = torch.randn([num_embeddings, embedding_dim])
W_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(W_attr, dtype=torch.float32), gain=1.0)
# 定义嵌入矩阵
self.W = torch.nn.Parameter(W_attr)
def forward(self, inputs):
# 根据索引获取对应词向量
embs = self.W[inputs]
return embs
emb_layer = Embedding(10, 5)
inputs = torch.tensor([0, 1, 2, 3])
emb_layer(inputs)
SRN层
该层有了嵌入层的铺垫,我们能够非常简单地得到模型的构建代码。
自己实现
import torch
import torch.nn as nn
import torch.nn.functional as F
torch.manual_seed(0)
# SRN模型
class SRN(nn.Module):
def __init__(self, input_size, hidden_size, W_attr=None, U_attr=None, b_attr=None):
super(SRN, self).__init__()
# 嵌入向量的维度
self.input_size = input_size
# 隐状态的维度
self.hidden_size = hidden_size
W_attr = torch.randn([input_size, hidden_size])
W_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(W_attr, dtype=torch.float32), gain=1.0)
U_attr = torch.randn([hidden_size, hidden_size])
U_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(U_attr, dtype=torch.float32), gain=1.0)
b_attr = torch.randn([1, hidden_size])
b_attr = torch.nn.init.xavier_uniform_(torch.as_tensor(b_attr, dtype=torch.float32), gain=1.0)
# 定义模型参数W,其shape为 input_size x hidden_size
self.W = torch.nn.Parameter(W_attr)
# 定义模型参数U,其shape为hidden_size x hidden_size
self.U = torch.nn.Parameter(U_attr)
# 定义模型参数b,其shape为 1 x hidden_size
self.b = torch.nn.Parameter(b_attr)
# 初始化向量
def init_state(self, batch_size):
hidden_state = torch.zeros([batch_size, self.hidden_size], dtype=torch.float32)
return hidden_state
# 定义前向计算
def forward(self, inputs, hidden_state=None):
# inputs: 输入数据, 其shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size = inputs.shape
# 初始化起始状态的隐向量, 其shape为 batch_size x hidden_size
if hidden_state is None:
hidden_state = self.init_state(batch_size)
# 循环执行RNN计算
for step in range(seq_len):
# 获取当前时刻的输入数据step_input, 其shape为 batch_size x input_size
step_input = inputs[:, step, :]
# 获取当前时刻的隐状态向量hidden_state, 其shape为 batch_size x hidden_size
hidden_state = F.tanh(torch.matmul(step_input, self.W) + torch.matmul(hidden_state, self.U) + self.b)
return hidden_state
# 初始化参数并运行
W_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1,0.2]]))
U_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1,0.0]]))
b_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
srn = SRN(2, 2, W_attr=W_attr, U_attr=U_attr, b_attr=b_attr)
inputs = torch.tensor([[[1, 0],[0, 2]]], dtype=torch.float32)
hidden_state = srn(inputs)
print("hidden_state", hidden_state)
结果如下:

torch框架实现
代码如下:
batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn(size=[batch_size, seq_len, input_size])
# 设置模型的hidden_size
hidden_size = 32
paddle_srn = nn.RNN(input_size, hidden_size)
self_srn = SRN(input_size, hidden_size)
self_hidden_state = self_srn(inputs)
paddle_outputs, paddle_hidden_state = paddle_srn(inputs)
print("self_srn hidden_state: ", self_hidden_state.shape)
print("torch_srn outpus:", paddle_outputs.shape)
print("torch_srn hidden_state:", paddle_hidden_state.shape)
结果如下:

比较
由于自己实现的SRN没有考虑多层的因素,所以比torch版本少了层次维度,因此其输出shape为[8, 32]。同时由于在以上代码使用pytorch内置API实例化SRN时,默认定义的是1层的单向SRN,因此其shape为[1, 8, 32],同时隐状态向量为[8,20, 32]。
接下来是模型的精度对比,两个计算结果如下:

可见精度比较接近。
另外,由于底层是由C++构建,torch自带的算子必然比我们构建的要快上很多。
线性层
线性层比较简单,我们直接使用torch.nn.Linear算子即可。
模型汇总
模型总体代码如下:
# 基于RNN实现数字预测的模型
class Model_RNN4SeqClass(nn.Module):
def __init__(self, model, num_digits, input_size, hidden_size, num_classes):
super(Model_RNN4SeqClass, self).__init__()
# 传入实例化的RNN层,例如SRN
self.rnn_model = model
# 词典大小
self.num_digits = num_digits
# 嵌入向量的维度
self.input_size = input_size
# 定义Embedding层
self.embedding = Embedding(num_digits, input_size)
# 定义线性层
self.linear = nn.Linear(hidden_size, num_classes)
def forward(self, inputs):
# 将数字序列映射为相应向量
inputs_emb = self.embedding(inputs)
# 调用RNN模型
hidden_state = self.rnn_model(inputs_emb)
# 使用最后一个时刻的状态进行数字预测
logits = self.linear(hidden_state)
return logits
# 实例化一个input_size为4, hidden_size为5的SRN
srn = SRN(4, 5)
# 基于srn实例化一个数字预测模型实例
model = Model_RNN4SeqClass(srn, 10, 4, 5, 19)
# 生成一个shape为 2 x 3 的批次数据
inputs = torch.tensor([[1, 2, 3], [2, 3, 4]])
# 进行模型前向预测
logits = model(inputs)
print(logits)
进行简单的模型计算得到最后一个位置的隐状态向量。这边测试结果如下:

模型训练
训练指定长度的数字预测模型
我们这边使用之前构造的Runner类能够很方便地进行模型训练和构造:
import os
import random
import torch
import numpy as np
from notawheel import Accuracy, RunnerV3
# 训练轮次
num_epochs = 500
# 学习率
lr = 0.001
# 输入数字的类别数
num_digits = 10
# 将数字映射为向量的维度
input_size = 32
# 隐状态向量的维度
hidden_size = 32
# 预测数字的类别数
num_classes = 19
# 批大小
batch_size = 8
# 模型保存目录
save_dir = "./checkpoints"
# 通过指定length进行不同长度数据的实验
def train(length):
print(f"\n====> Training SRN with data of length {length}.")
# 固定随机种子
np.random.seed(0)
random.seed(0)
torch.manual_seed(0)
# 加载长度为length的数据
data_path = f"datasets/{length}"
train_examples, eval_examples, test_examples = load_data(data_path)
train_set, eval_set, test_set = DigitSumDataset(train_examples), DigitSumDataset(eval_examples), DigitSumDataset(test_examples)
train_loader = torch.utils.data.DataLoader(train_set, batch_size=batch_size)
eval_loader = torch.utils.data.DataLoader(eval_set, batch_size=batch_size)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)
# 实例化模型
base_model = SRN(input_size, hidden_size)
model = Model_RNN4SeqClass(base_model, num_digits, input_size, hidden_size, num_classes)
# 指定优化器
optimizer = torch.optim.Adam(model.parameters(), lr)
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = nn.CrossEntropyLoss()
# 基于以上组件,实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)
# 进行模型训练
model_save_path = os.path.join(save_dir, f"best_srn_model_{length}.pt")
runner.train(train_loader, eval_loader, num_epochs=num_epochs, eval_steps=100, log_steps=100, save_path=model_save_path)
return runner
部分运行结果如下,准确率在25%浮动:

模型训练时的损失如下:
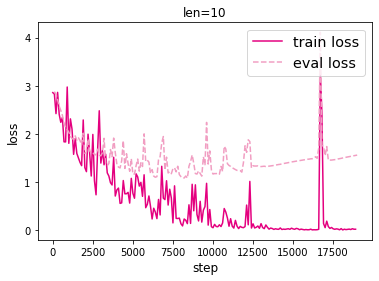
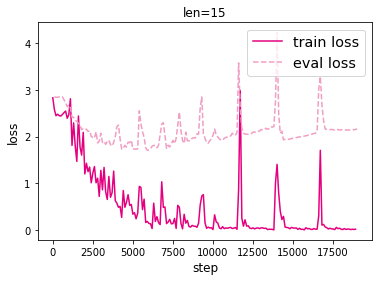

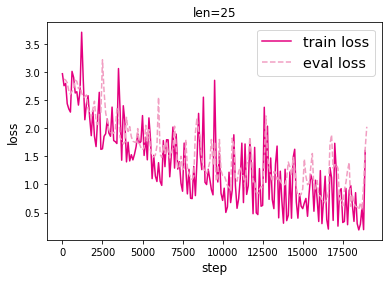
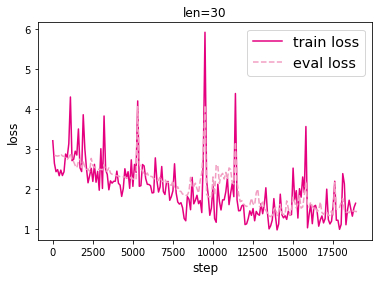

模型评价
模型评价代码如下:
srn_eval_scores = []
srn_test_scores = []
for length in lengths:
print(f"Evaluate SRN with data length {length}.")
runner = srn_runners[length]
# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, f"best_srn_model_{length}.pt")
runner.load_model(model_path)
# 加载长度为length的数据
data_path = f"./datasets/{length}"
train_examples, eval_examples, test_examples = load_data(data_path)
test_set = DigitSumDataset(test_examples)
test_loader = DataLoader(test_set, batch_size=batch_size)
# 使用测试集评价模型,获取测试集上的预测准确率
score, _ = runner.evaluate(test_loader)
srn_test_scores.append(score)
srn_eval_scores.append(max(runner.eval_scores))
for length, eval_score, test_score in zip(lengths, srn_eval_scores, srn_test_scores):
print(f"[SRN] length:{length}, eval_score: {eval_score}, test_score: {test_score: .5f}")
输出结果如下:

我们将准确率可视化,结果如下:
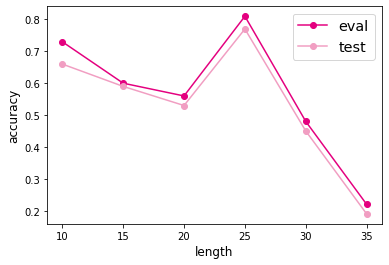
写在最后
通过本次实验,我们了解了简单的循环神经网络结构。通过实现SRN并进行实验,测试了循环神经网络的记忆能力。通过构建嵌入层、SRN等最终得到模型。尽管效果不是很好,但是基本的思路非常清晰。
![[机器人学习]-树莓派6R机械臂运动学分析](https://img-blog.csdnimg.cn/ab23a9b9c6e646bfa5d182dc7a6c4622.png)








![[强网杯 2019]Upload](https://img-blog.csdnimg.cn/91730e9a762e42f9bd84048ef1d4c09d.png)