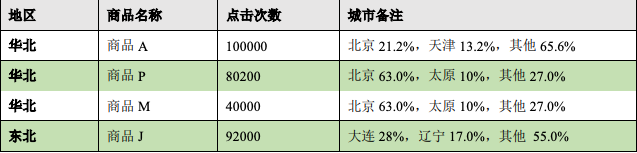
本文重点

当数据从n维降到k维的时候，我们需要找到一个能使得投影误差最小的k维向量构成的投影平面，然后将数据进行投影，从而达到降维的作用。所以PCA算法要做的就是两件事情，一件事情就是计算最优的k维向量，另一个问题就是计算原来样本点映射到降维面的z(i),也就是这些新的特征变量。

第一件事情

第一步：均值归一化

第二步：计算协方差的矩阵sigma（n*n）

 

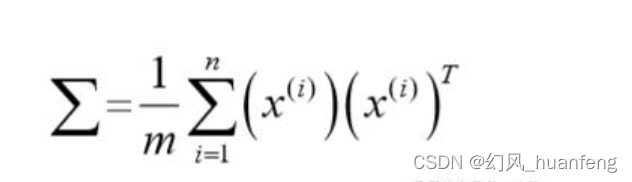
协方差矩阵公式

其中x(i)表示第i个样本，是一个列向量。

第三步：计算出协方差矩阵的特征向量。利用奇异值分解来求解，[U, S, V]= svd(sigma)。它会返回三个矩阵，我们需要U矩阵（n*n）矩阵（特征向量构成的矩阵）

 

 

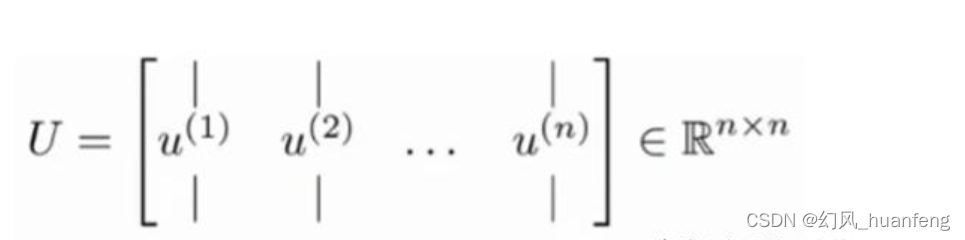
U矩阵中的每一列都是我们要的特征向量， 是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们想要从n维降低到k维，那么我们只用取前k列向量，这样我们就得到了u(1)、u(2)…u(k)，这k个向量就是我们用来投影的k个方向。

现在第