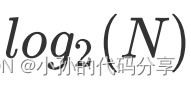1. 简介

动态规划是一种算法思想； 动态规划=递归式+子问题

1.1 案例1： 斐波那契数列

• 斐波那契数列：Fn=Fn-1+Fn-2

代码演示： 使用递归和非递归的方法来求解斐波那契数列的第n项；

递归的方法：

   public static int fbnc(int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        return fbnc(n - 1) + fbnc(n - 2);
    }

非递归的方法：

    public static Long fbnc2(int n) {
        ArrayList<Long> list = new ArrayList<>();
        list.add(0L);
        list.add(1L);
        list.add(1L);
        if (n > 2) {
            for (int i = 0; i < n - 2; i++) {
                long num = list.get(list.size() - 1) + list.get(list.size() - 2);
                list.add(num);
            }
        }
        return list.get(n);
    }

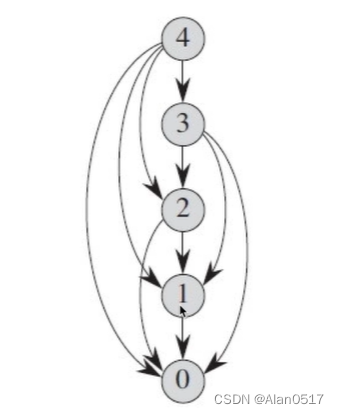
对比发现，递归其实相比之下很慢递归子问题重复计算，假设n=6,是否递归存在子问题的重复计算：

• f(6)=f(5)+f(4)
  f(5)=f(4)+f(3)
  f(4)=f(3)+f(2)
  f(4)=f(3)+f(2)
  f(3)=f(2)+f(1)
  f(3)=f(2)+f(1)
  f(3)=f(2)+f(1)
  f(2)=1

1.2 案例2：钢条切割问题

• 某公司出售钢条，出售价格与钢条长度之间的关系如下表：
  
  问题：现在有一段长度为n的钢条和上面的价格表，求切割钢条方案，使得总收益最大；
  假设现在钢条长度是4米，那么所有切割的方案如下：
  
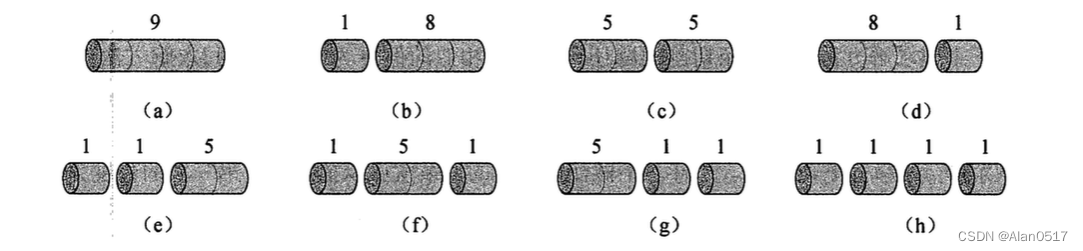
  如上图所示，长度为4的时候，有8种切割方案，当长度为n的时候
  

1.2.1 递推式：

长度为n的钢条切割后最优收益为rn,可以得出

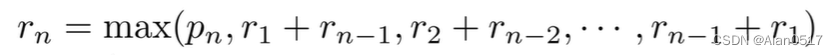
• 第一个参数Pn 表示不切割；
• 其他n-1 个参数分别表示另外n-1种不同切割方案，对方案i=1,2,n-1
  • 将钢条切割为长度为 i 和 n-i 两段；
  • 方案i 的收益为切割两段的最优收益之和；
• 考察所有的i,选择其中收益最大的方案；
• 代码如下：

    public static void main(String[] args) {
        int[] arr = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
        System.out.println("getMaxValue(arr,9) = " + getMaxValue(arr, 9));
    }
    
    public static int getMaxValue(int[] arr, int n) {
        if (n == 0) {
            return 0;
        }else {
            int res = arr[n];
            for (int i = 1; i < n; i++) {
                res = Math.max(res, getMaxValue(arr, i) + getMaxValue(arr, n - i));
            }
            return res;
        }
    }

1.2.2 最优子结构

• 可以将求解规模为n的原问题，划分为规模更小的子问题：完成依次切割后，可以将产生的两段钢条看成两个独立的钢条切割问题；
• 组合两个子问题的最优解，并在所有可能的两段分割方案中选取组合收益最大的，构成原问题的最优解；
• 钢条切割满足最优子结构，问题的最优解由相关子问题的最优解组合而成，这些子问题可以独立求解；
• 钢条切割问题还存在更简单的递归求解方法
  • 从钢条的左边切割下长度为i的一段，只对右边剩下的一段继续进行切割，左边的不再切割；
  • 递推式简化为
    
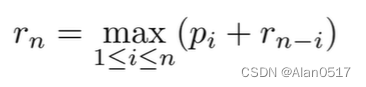
  • 不做切割的方案就可以描述为：左边一段长度为n,收益为pn，剩余一段长度为0，收益为r0=0
  • 代码如下所示：

    public static void main(String[] args) {
        int[] arr = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
        System.out.println("getMaxValue(arr,9) = " + getMaxValue(arr, 9));
    }

    public static int getMaxValue(int[] arr, int n) {
        if (n == 0) {
            return 0;
        } else {
            int res = 0;
            for (int i = 1; i < n + 1; i++) {
                res = Math.max(res, arr[i] + getMaxValue(arr, n - i));
            }
            return res;
        }
    }

1.2.3 自顶向下递归实现

• 为什么自顶向下递归写出来的算法效率低下，因为存在子问题重复问题，时间复杂度是O(2^n)
  
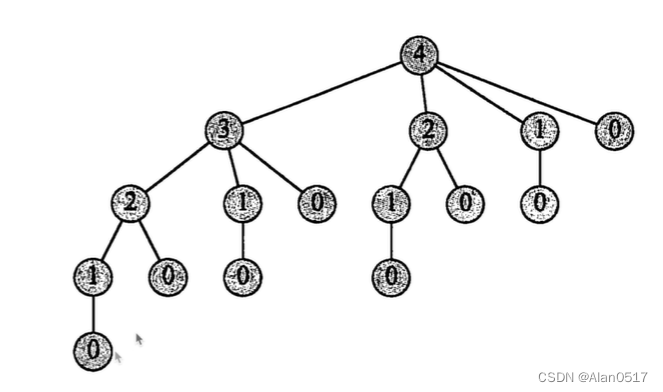
  由于递归算法重复求解相同子问题，效率低下；动态规划思想：每个子问题只求解一次，保存求解结果，之后需要此问题时，只需查找保存的结果即可；

    public static void main(String[] args) {
        int[] arr = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
        System.out.println("getMaxValue(arr,9) = " + getMaxValue(arr, 9));
    }
    
    public static int getMaxValue(int[] arr, int n) {
        if (n == 0) {
            return 0;
        }else {
            int res = arr[n];
            for (int i = 1; i < n; i++) {
                res = Math.max(res, getMaxValue(arr, i) + getMaxValue(arr, n - i));
            }
            return res;
        }
    }

1.2.4 自下而上实现

• 时间复杂度O(n^2)
  

    public static void main(String[] args) {
        int[] arr = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
        System.out.println("getMax(arr,9) = " + getMax(arr, 9));
    }


    public static int getMax(int[] arr, int n) {
        List<Integer> list = new ArrayList<>();
        list.add(0);
        for (int i = 1; i < n + 1; i++) {
            int res = 0;
            for (int j = 1; j < i + 1; j++) {
                res = Math.max(res, arr[j] + list.get(i - j));
            }
            list.add(res);
        }
        return list.get(n);
    }

1.2.5 获取最优解的切割方式

基于原来的代码，将具体的切割方式打印出来

 public static void main(String[] args) {
        int[] arr = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30};
        System.out.println("getMax(arr,9) = " + getMaxExtend(arr, 9));
    }
    
    public static List<Integer> getMaxExtend(int[] arr, int n) {
        List<Integer> result = new ArrayList<>();
        result.add(0);
        List<Integer> typeList = new ArrayList<>();
        typeList.add(0);

        for (int i = 1; i < n + 1; i++) {
            int res = 0;  //价格的最大值
            int type = 0;
            for (int j = 1; j < i + 1; j++) {
                if (arr[j] + result.get(i - j) > res) {
                    res = arr[j] + result.get(i - j);
                    type = j;
                }
            }
            result.add(res);
            typeList.add(type);
        }
        List<Integer> objects = new ArrayList<>();
        while (n > 0) {
            objects.add(typeList.get(n));
            n = n - typeList.get(n);
        }
        return objects;
    }