前言

上回我们知道HandlerMapping是用来寻找Handler的，并不与Handler的类型或者实现绑定，而是根据需要定义的。那么为什么要单独给@RequestMapping实现一个HandlerMapping？这次咱们就来专门看看这个RequestMappingHandlerMapping。

RequestMappingHandlerMapping

名字来源

因为RequestMappingHandlerMapping是专门为@RequestMapping而生的，因此他的名字是这样来的：@RequestMapping的HandlerMapping了。
为什么不叫MethodHandlerMapping呢？主要还是Handler是一个逻辑概念，MethodHandler了只是对目标方法进行了封装，并不是真正处理请求的。真正处理请求的是我们@RequestMapping的方法。取个名字都给你讲道理。

@RequestMapping

在解答文章开头的问题前，我们先看看@RequestMapping

@Target({ElementType.TYPE, ElementType.METHOD})
@Retention(RetentionPolicy.RUNTIME)
@Documented
@Mapping
public @interface RequestMapping {
	/**
	 * 处理器的名字，支持类级别和方法级别，多个路径用#分割
	 */
	String name() default "";
	/**
	 * 匹配请求路径
	 */
	@AliasFor("path")
	String[] value() default {};
	/**
	 * 匹配请求路径
	 */
	@AliasFor("value")
	String[] path() default {};
	/**
	 * Http请求方法：可选GET, POST, HEAD, OPTIONS, PUT, PATCH, DELETE, TRACE
	 */
	RequestMethod[] method() default {};
	/**
	 * 匹配指定的地址栏参数
	 */
	String[] params() default {};

	/**
	 * 匹配特定的header
	 */
	String[] headers() default {};
	/**
	 * 匹配特定的Content-Type
	 */
	String[] consumes() default {};
	/**
	 * 匹配特定的Accept
	 */
	String[] produces() default {};
}

发现了吗，各位？他除了能根据URI匹配，还能根据请求头、请求方法、甚至是请求参数来匹配！上回说的基于URL的两种HandlerMapping都不能满足他，因此必须推出一个更加强大、可扩展性更强的HandlerMapping——RequestMappingHandlerMapping
在这里插入图片描述
那么问题来了：

@RequestMapping是在什么如何被解析的呢？
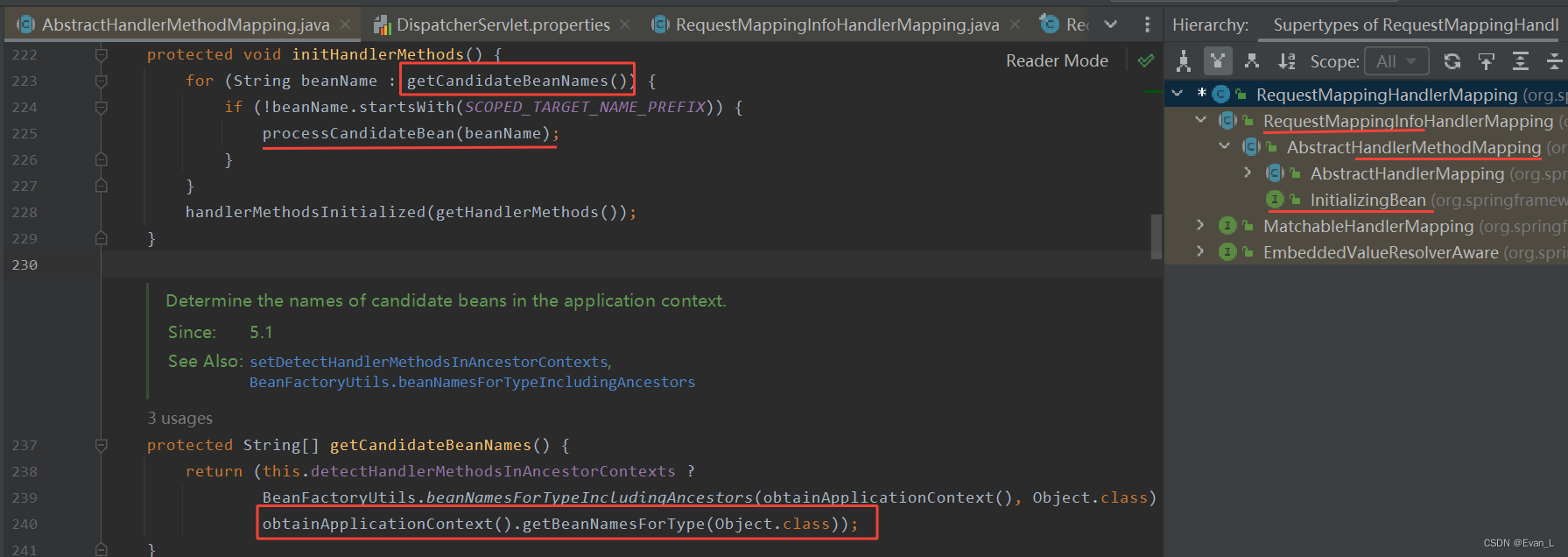
我们很容易想到的就是，遍历容器中所有的对象，检查是否存在@Controller注解。存在，那就是控制器。然后接着遍历所有声明的public方法，检查是否存在@RequestMapping方法。这样，我们就找到了处理器方法。
@RequestMapping是在什么时候被解析的呢？
本着“谁使用，谁解析”的原则，他自然是被RequestMappingHandlerMapping解析的。而又因为@RequestMapping的寻找可太费功夫，不可能在提供映射服务时再来解析，只能是初始化时进行解析。因此实现InitializingBean进行初始化，是个选择。

没错，实际上，SpringMVC跟你想的一样。在InitializingBean的afterPropertiesSet方法中，完成了以3下件事：

寻找@Controller的bean，并找到所有的@RequestMapping方法
解析@RequestMapping封装成RequestMappingInfo

将以上解析到的信息进行注册。信息包括：

信息	描述
@Controller/@RequestMapping对象	反射调用目标方法时，需要的target对象
RequestMappingInfo	由@RequestMapping解析而来
@RequestMapping的方法	注册时，注册器会将Method与handler对象一起封装成HandlerMethod进行注册。便于后面适配器调用。

@RequestMapping的注册

前面的解析@RequestMapping到RequestMappingInfo，可以省略，比较简单。但是@RequestMapping的注册没办法省略。因为如果搞不清楚他是怎么注册的，也就没办法理解他是怎么寻找目标处理器的。

为了支撑@RequestMapping多样化的匹配条件，不能再像前面两款HanderMapping一样，简单粗暴的使用Map了。在org.springframework.web.servlet.handler.AbstractHandlerMethodMapping的内部定义了内部类，专门用来做注册中心，管理映射关系。

	/**
	 * Mapping注册中心，可以理解为办事处
	 */
	class MappingRegistry {
		/**
		 * T是匹配条件的对象。MappingRegistration是注册的信息，可以理解为你要做事情。
		 * 对于RequestMappingHandlerMapping，T就是RequestMappingInfo
		 * MappingRegistration包括信息：RequestMappingInfo、HandlerMethod、directPaths、mappingName、corsConfig
		 */
		private final Map<T, MappingRegistration<T>> registry = new HashMap<>();
		/**
		 * Map<path, RequestMappingInfo>
		 */
		private final MultiValueMap<String, T> pathLookup = new LinkedMultiValueMap<>();

		/**
		 * Map<mappingName, List<HandlerMethod>>
		 */
		private final Map<String, List<HandlerMethod>> nameLookup = new ConcurrentHashMap<>();
	}

从他的属性，我们可以分析得到如下信息：

直接通过请求路径来查找处理器时，需要经过pathLookup中转registry，最后拿到MappingRegistration才到达HandlerMethod.
直接通过mappingName则可以直接找到HandlerMethod. 不过这个是Spring为了支持<%@ taglib uri="http://www.springframework.org/tags" prefix="s" %>而提供的。跟我们平时使用没多大关系。

但是各位观众老爷，pathLookup找到的是一个，而mappingName能找到多个，这是咋回事？误会啊，pathLookup的value可不是简单的一个元素，而是多个！他是MultiValueMap，不是我们经常看到的地摊货HashMap。他可以一个key对应多个value。

但是为什么会有多个呢？或者说为什么需要保存多个呢？
因为一个Handler可以处理多个请求，如果由多个Handler都能处理某一个请求的时候怎么办呢？况且SpringMVC还支持通配符匹配。umm…这一幕有点似曾相识，我们的nginx做路由转发的时候，不是也有类似的问题吗？这意味着在查找Handler的时候，我们还需要找到最佳的匹配。例如，/*相较于/hello，那肯定是/hello更精确，更合适啦。你看，多严谨！

总结

由于@RequestMapping支持灵活的请求匹配条件，而不只是简单的路径，只能开发出RequestMappingHandlerMapping进行支持。
RequestMappingHandlerMapping是通过InitializingBean进行初始化的，在这里完成@RequestMappingHandlerMapping的扫描和解析，以及注册。
HandlerMethod是在注册时进行封装的。获取Handler时，拿到的Handler就是HandlerMethod。后面的适配器适配的，也是他。

后记

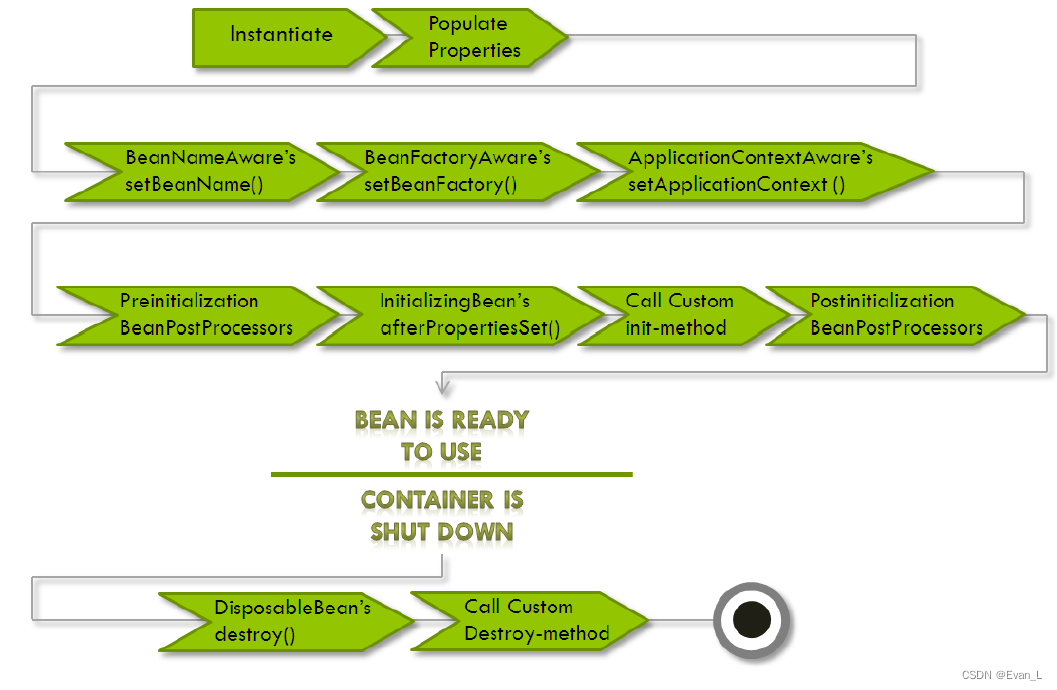
RequestMappingHandlerMapping使用了InitializingBean做初始化，但是当我们自己在做初始化的时候，尤其是使用多种初始化方式的时候，应当要注意Spring的调用顺序，否则有可能发生NPE，或者获取不到目标属性的情况。例如：同时在ApplicationContextAware、InitializingBean、@PostConstruct进行初始化。
为此，给大家找了官方的bean的生命周期
在这里插入图片描述
上一篇：
探索SpringMVC-DispatcherServlet之HandlerMapping
第一篇：
探索SpringMVC-web上下文