文章目录
- 一、spfa 算法
- 1. spfa 算法简介
- 2. spfa 算法和 bellman-ford 算法的区别
- 3. spfa 算法和 dijkstra 算法的区别
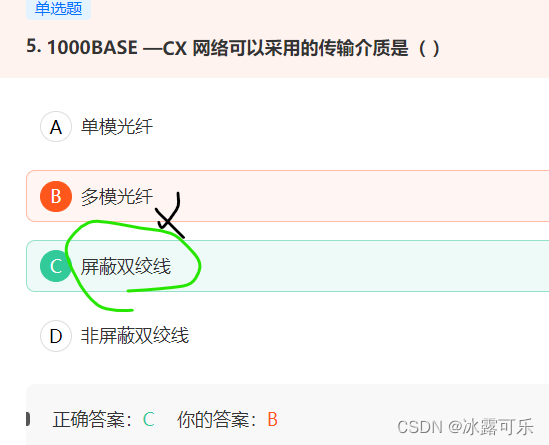
- 4. spfa 算法实现步骤
- 5. spfa 算法举例图解
- 6. spfa 算法用于求最短路和判断负环,详见下面两道例题。
- 二、spfa 算法例题—— spfa 求最短路
- 具体实现
- 1. 样例演示
- 2. 实现思路
- 3. 代码注解
- 4. 实现代码
- 三、spfa 算法例题—— spfa 判断负环
- 具体实现
- 1. 实现思路
- 2. 代码注解
- 3. 实现代码
一、spfa 算法
1. spfa 算法简介
- spfa 算法是 bellman-ford 算法的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。spfa 最坏情况下时间复杂度和朴素 bellman-ford 相同,为 O(nm)。
- 在这里,我们需要明确一下 松弛 的概念:
- 节点 u 以及它的邻节点 v,从起点跑到邻节点 v 有好多跑法,有的跑法经过 u ,有的不经过。
- 经过节点 u 的跑法的距离就是 dist[u] + 节点 u 到邻节点 v 的距离。
- 松弛操作,就是看一看 dist[v] 和 dist[u] + 节点 u 到邻节点 v 的距离哪个大一点。
- 如果前者大一点,就说明当前的不是最短路,就要赋值为后者,这就叫做松弛。
2. spfa 算法和 bellman-ford 算法的区别
- bellman-ford 算法具体讲解详见搜索与图论 - bellman-ford 算法。
- (1)bellman-ford 算法中,循环 n 次,每次遍历 m 条边,每次遍历的时候,把入度的点的距离更新成最小。但是,这样就循环遍历了很多用不到的边。比如第一次遍历,只有第一个点的临边是有效的。
- (2) 因此,spfa 算法中,采用邻接表的方式,只用到有效的点(更新了临边的点),直到每个点都是最短距离为止。采用队列优化的方式存储每次更新了的点,每条边最多遍历一次。如果存在负权回路,从起点 1 出发,回到 1 距离会变小, 会一直在三个点中循环。
- 因此,便会产生一个疑问,我们不用队列,直接遍历所有的点可以吗?
- 这样操作似乎不行,因为是更新了点之后,这个点的邻边才可以用,如果没有更新到循环的点,那么循环的点也是不可用的。
3. spfa 算法和 dijkstra 算法的区别
- dijkstra 算法具体讲解详见搜索与图论 - dijkstra 算法。
- (1)在 spfa 算法当中,st 数组用来检验队列中是否有重复的点。
- spfa 算法从队列中使用了当前的点,会把该点 pop 掉,状态数组 st[i] = false (说明堆中不存在了) ,更新邻边之后,把邻边放入队列中, 并且设置状态数组为 true,表示放入队列中 。如果当前的点距离变小,可能会再次进入队列,因此可以检验负环。
- 每次更新可以记录一次,如果记录的次数 > n,代表存在负环(环一定是负的,因为只有负环才会不断循环下去)。
- (2) 在 dijkstra 算法当中,st是一个集合,不是检验队列中的点。
- dijkstra 算法使用当前点更新邻边之后,把该点加入到一个集合中,使用该点更新邻边,并把邻边节点和距离起点的距离置入堆中(不设置状态数组)。下一次从堆中取最小值,并把对应的节点放入集合中,继续更新邻边节点,直到所有的点都存入集合中。因此 dijkstra 算法不判断负环。
- 从上述描述中能看出,dijkstra 算法存放节点的堆,具有单调性,而 spfa 算法的队列不需要具有单调性。
| 算法名称 | 对应问题 |
|---|---|
| dijkstra 算法 | 只能处理带正权边的图 |
| bellman-ford 算法 | 可以处理任意带负权边和负权环的图 |
| spfa 算法 | 可以处理带负权边的图 |
4. spfa 算法实现步骤
- (1) 建立一个队列,初始时队列里只有起始点。
- (2) 建立一个数组记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为 0)。
- (3) 建立一个数组,标记点是否在队列中。
- (4) 队头不断出队,计算始点起点经过队头到其他点的距离是否变短,如果变短且被点不在队列中,则把该点加入到队尾。
- (5) 重复执行直到队列为空。
- (6) 在保存最短路径的数组中,就得到了最短路径。
5. spfa 算法举例图解
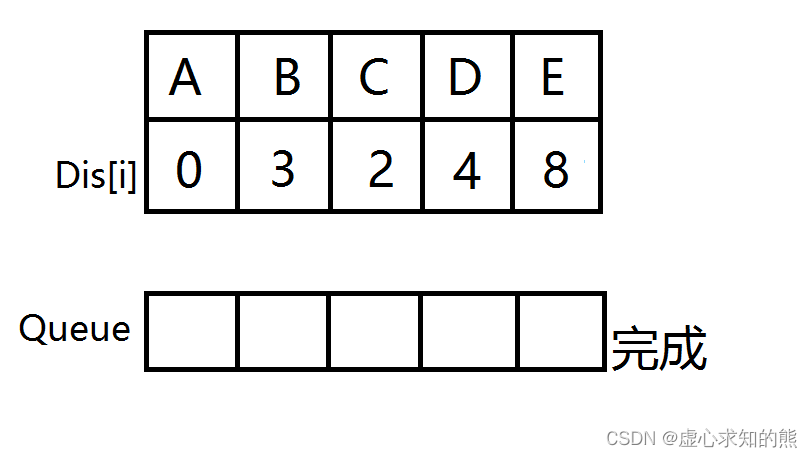
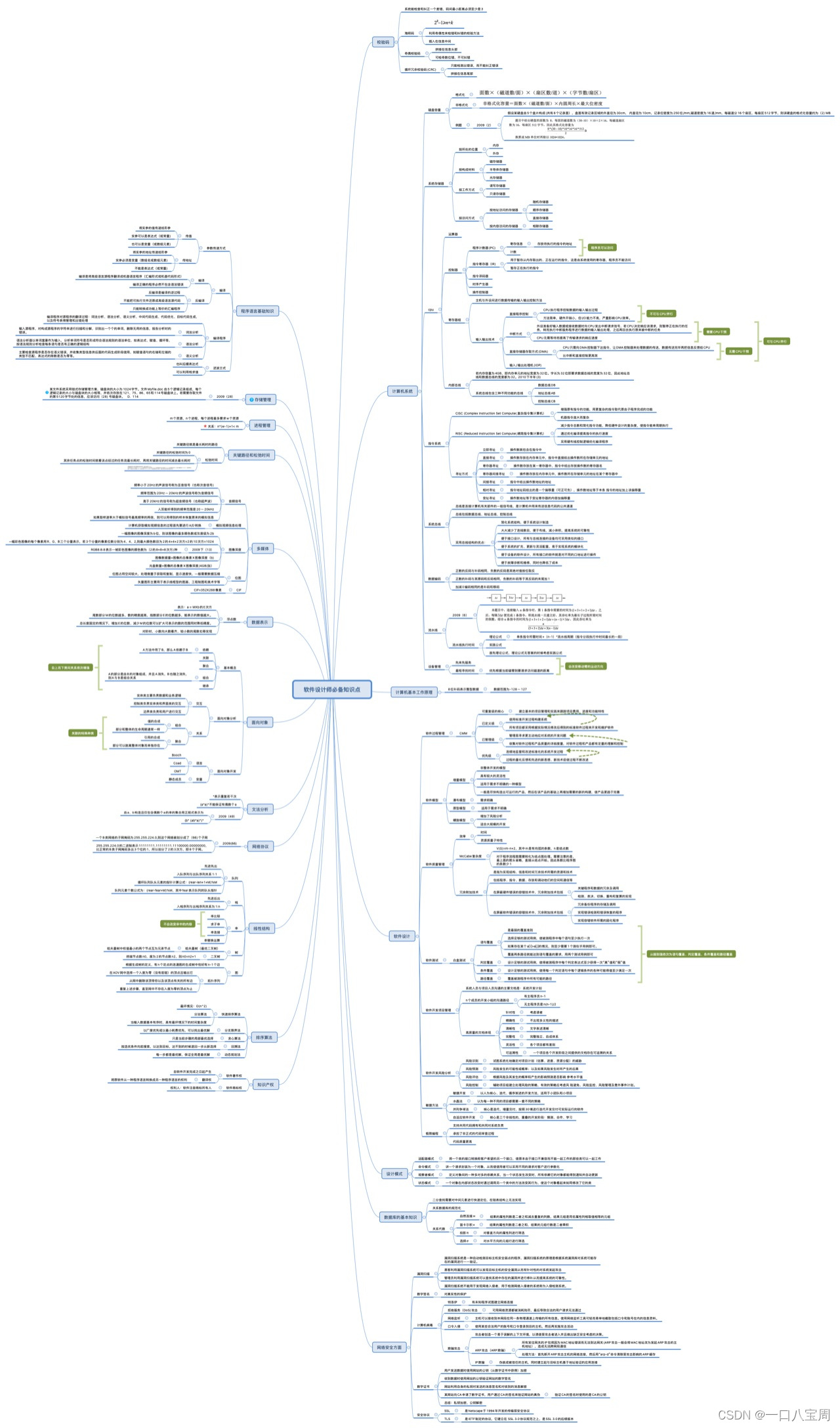
- 给定一个有向图,如下,求 A~E 的最短路。
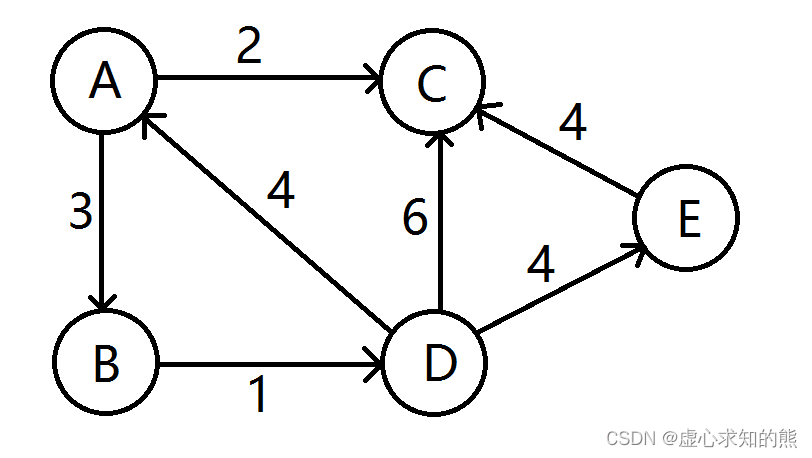
- 节点 A 首先入队,然后节点 A 出队,计算出到节点 B 和节点 C 的距离会变短,更新距离数组,节点 B 和节点 C 没在队列中,节点 B 和节点 C 入队。
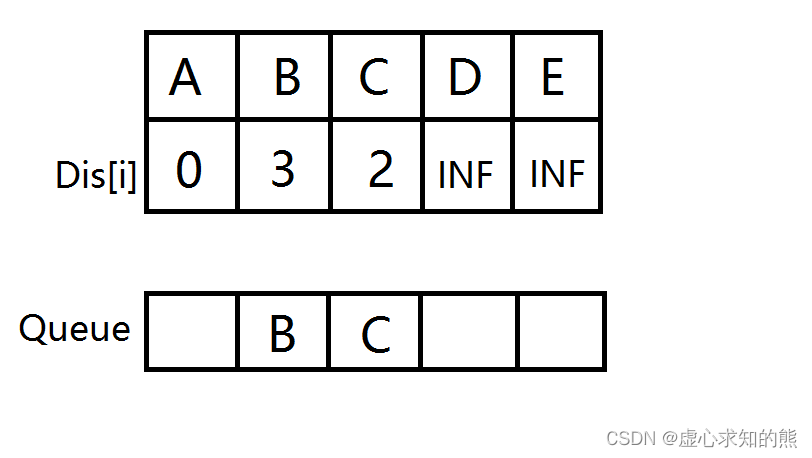
- 节点 B 出队,计算出到节点 D 的距离变短,更新距离数组,节点 D 没在队列中,节点 D 入队。然后节点 C 出队,无点可更新。
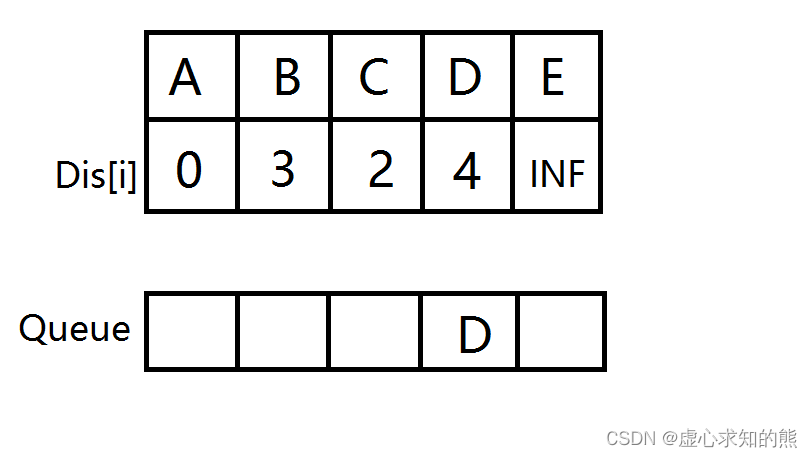
- 节点 D 出队,计算出到节点 E 的距离变短,更新距离数组,节点 E 没在队列中,节点 E 入队。
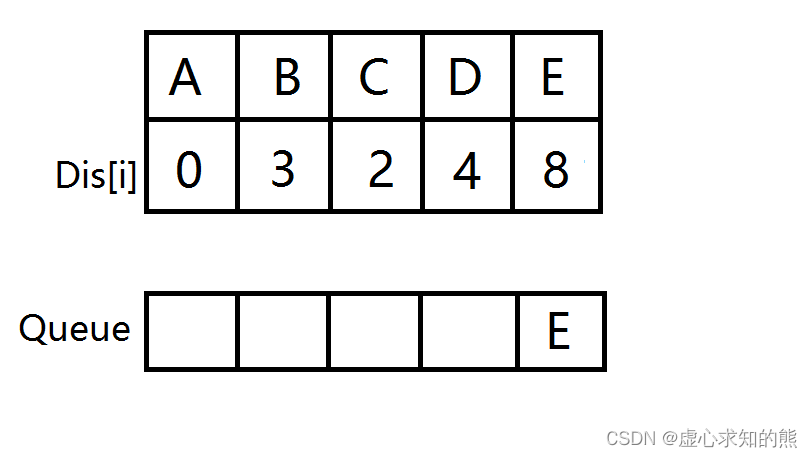
- 节点 E 出队,此时队列为空,源点到所有点的最短路已被找到,最短路即为 8。
6. spfa 算法用于求最短路和判断负环,详见下面两道例题。
二、spfa 算法例题—— spfa 求最短路
题目描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 impossible。
数据保证不存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 impossible。
数据范围
1 ≤ n,m ≤ 1e5
图中涉及边长绝对值均不超过 10000。
输入样例
3 3
1 2 5
2 3 -3
1 3 4
输出样例
2
具体实现
1. 样例演示
- 输入 n = 3,m = 3,表示求从 1 号点到 n = 3 号点的最短距离,共有 m = 3 条边。
- 从 1 号点到 2 号点的边长为 5 。
- 从 2 号点到 3 号点的边长为 -3 。
- 从 1 号点到 3 号点的边长为 4 。
- 显然,最短路径是 2 。
2. 实现思路
- 详见 spfa 算法举例图解。
3. 代码注解
- int h[N], w[N], e[N], ne[N], idx;使用邻接表来存储图。
- int dist[N];保存最短路径的值。
- int q[N], hh, tt = -1;表示队列。
- memset(h, -1, sizeof h);初始化邻接表。
- memset(dist, 0x3f, sizeof dist);初始化距离。
- 其他代码已经标记在实现代码当中。
4. 实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int h[N], e[N], w[N], ne[N], idx;//邻接表,存储图
int st[N];//标记顶点是不是在队列中
int dist[N];//保存最短路径的值
int q[N], hh, tt = -1;//队列
//图中添加边和边的端点
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
idx++;
}
void spfa()
{
tt++;
q[tt] = 1;//从1号顶点开始松弛,1号顶点入队
dist[1] = 0;//1号到1号的距离为 0
st[1] = 1;//1号顶点在队列中
//不断进行松弛
while(tt >= hh)
{
int a = q[hh];//取对头记作a,进行松弛
hh++;
st[a] = 0;//取完队头后,a不在队列中了
for(int i = h[a]; i != -1; i = ne[i])//遍历所有和a相连的点
{
//获得和a相连的点和边
int b = e[i], c = w[i];
//如果可以距离变得更短,则更新距离
if(dist[b] > dist[a] + c)
{
//更新距离
dist[b] = dist[a] + c;
//如果没在队列中
if(!st[b])
{
tt++;
q[tt] = b;//入队
st[b] = 1;//打标记
}
}
}
}
}
int main()
{
memset(h, -1, sizeof h);//初始化邻接表
memset(dist, 0x3f, sizeof dist);//初始化距离
int n, m;//保存点的数量和边的数量
cin >> n >> m;
//读入每条边和边的端点
for(int i = 0; i < m; i++)
{
int a, b, w;
cin >> a >> b >> w;
//加入到邻接表
add(a, b, w);
}
spfa();
if(dist[n] == 0x3f3f3f3f )//如果到n点的距离是无穷,则不能到达
{
cout << "impossible";
}
else
{
cout << dist[n];//否则能到达,输出距离
}
system("pause");
return 0;
}
三、spfa 算法例题—— spfa 判断负环
题目描述
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环, 边权可能为负数。
请你判断图中是否存在负权回路。
输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点 y 的有向边,边长为 z。
输出格式
如果图中存在负权回路,则输出 Yes,否则输出 No。
数据范围
1 ≤ n ≤ 2000
1 ≤ m ≤ 10000
图中涉及边长绝对值均不超过 10000。
输入样例
3 3
1 2 -1
2 3 4
3 1 -4
输出样例
Yes
具体实现
1. 实现思路
- 判断负环的方法和 bellman-ford 算法相同,应用抽屉原理。
- 抽屉原理: 如果每个抽屉代表一个集合,每一个苹果就可以代表一个元素,假如有n+1个元素放到n个集合中去,其中必定有一个集合里至少有两个元素。
- 如果一个点在被入队次数大于 n 次,那么说明存在负环。
- 原理是虽然一个点在状态数组会被多次更新,但是它的更新次数不会大于 n-1 次,因为从一个点到另一个点最多经过 n-1 条边。如果存在负环则会造成无限入队的情况,spfa 算法陷入死循环,这时候就可直接退出了。
- 个人理解:如果某一个点的 cnt >= n 的话说明这个点还没到最后一个点的时候就已经有了 n 条边了,早就已经符合出现负环的情况了。
- (1) dist[x] 记录虚拟源点到 x 的最短距离。
- (2) cnt[x] 记录当前 x 点到虚拟源点最短路的边数,初始每个点到虚拟源点的距离为 0 ,只要他能再走 n 步,即 cnt[x] >= n,则表示该图中一定存在负环,由于从虚拟源点到 x 至少经过 n 条边时,则说明图中至少有 n + 1 个点,表示一定有点是重复使用。
- (3) 若 dist[j] > dist[t] + w[i],则表示从 t 点走到 j 点能够让权值变少,因此进行对该点 j 进行更新,并且对应 cnt[j] = cnt[t] + 1,往前走一步。
2. 代码注解
- int dist[N], cnt[N];记录每个点到起点的边数,当 cnt[i] >= n 表示出现了边数 >= 结点数,必然有环,而且一定是负环。
- bool st[N];判断当前的点是否已经加入到队列当中了;已经加入队列的结点就不需要反复的把该点加入到队列中了,就算此次还是会更新到起点的距离,那只用更新一下数值而不用加入到队列当中,意味着,st数组起着提高效率的作用,不在乎效率的话,去掉也可以。
- 其他代码注解已经标记在实现代码当中。
3. 实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 2010, M = 10010;
int n, m;
int h[N], w[M], e[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];
void add(int a, int b, int c)
{
e[idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
idx ++ ;
}
bool spfa()
{
queue<int> q;
for (int i = 1; i <= n; i ++ )
{
st[i] = true;
q.push(i);
}
//队列中的点用来更新其他点到起点的距离
while (q.size())
{
int t = q.front();
q.pop();
//t出队,标记出队
st[t] = false;
//更新与t邻接的边
for (int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[t] + w[i])
{
//结点j可以通过中间点t降低距离
dist[j] = dist[t] + w[i];
//那么结点j在中间点t的基础上加一条到自己的边
cnt[j] = cnt[t] + 1;
//边数不小于结点数,出现负环,函数结束
if (cnt[j] >= n)
{
return true;
}
//若此时j没在队列中,则进队。
//已经在队列中了,上面已经更新了数值。重复加入队列降低效率
if (!st[j])
{
//j进队,标记进队
q.push(j);
st[j] = true;
}
}
}
}
//走到这了,函数还没结束,意味着边数一直小于结点数,不存在负环
return false;
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof h);
while (m -- )
{
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
if (spfa())
{
puts("Yes");
}
else
{
puts("No");
}
system("pause");
return 0;
}








![[强网杯 2019]Upload](https://img-blog.csdnimg.cn/91730e9a762e42f9bd84048ef1d4c09d.png)