前导知识：
概率密度函数（密度函数）：描述一个随机变量的在某个确定的取值点附近的可能性的函数。
随机变量的取值落在某个区域内的概率为概率密度函数在这个区域上的积分。
性质：
f(x)>=0
数学期望
又称均值，是实验中每次结果的概率乘以其结果的总和，反映随机变量平均取值的大小。
大数定律(在随机事件的大量重复中，往往呈现几乎必然的规律) 表示，随着重复次数接近无穷大，数值的算术平均值几乎肯定收敛于期望值。
随机变量取值为Xi,概率为pk，则期望公式：
方差
方差描述数据的离散程度
正态分布：
如果一个随机变量X服从一个数学期望为u，方差为σ2的正态分布，则记为N（u，σ2）
正态分布的概率密度为
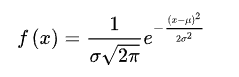
随着u和σ变化，概率分布也产生变化。
分布情况
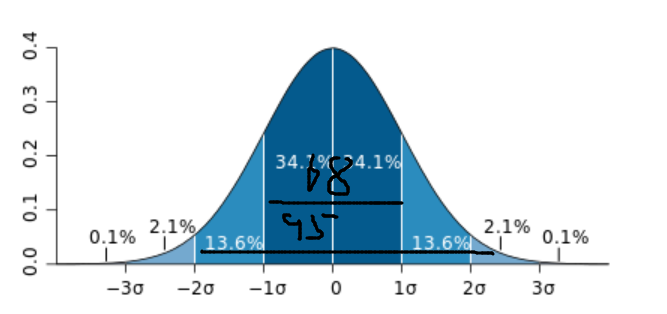
![[2022-12-17]神经网络与深度学习第5章 - 循环神经网络(part 1)](https://img-blog.csdnimg.cn/50a2576319ce444ca3dbf777500e7a2f.png#pic_center)
![[机器人学习]-树莓派6R机械臂运动学分析](https://img-blog.csdnimg.cn/ab23a9b9c6e646bfa5d182dc7a6c4622.png)
