根据9月3日的报道,苹果即将推出的iPhone 15系列将不再使用皮革保护壳,取而代之的将是一种名为"FineWoven"的新材料编织工艺保护壳。

这种保护壳将有十种颜色可供选择,包括黑色、桑葚色、灰褐色、常绿色、太平洋蓝色、紫藤色、古白色、黄油黄色、橙色和粉色。
从网上流传的疑似新款手机壳的图片中可以看出,这种保护壳的边缘包裹着橡胶,颜色稍微深一些。不仅如此,这种全新的材料还将用于苹果新款的Apple Watch表带。
据称,苹果公司计划在Apple Watch Series 9中推出一款新的磁性扣子编织布料表带,与新款iPhone手机壳相同材料制成。这款表带将提供更多的颜色选择,让用户可以根据个人喜好来配搭和展示他们的苹果设备。这款磁性表带的售价将为99美元(约合720元人民币)。这将成为苹果设备的最新配件之一。
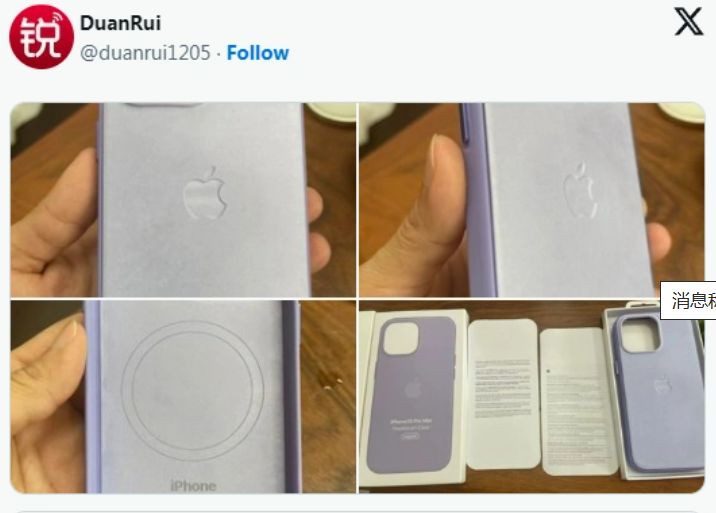
与此同时,传言称苹果可能会取消iPhone 15系列的皮革手机壳,取而代之的编织布料外观的替代品。这种"FineWoven"材料的出现给用户带来了更多的选择。根据消息,苹果公司将于9月13日凌晨1点举行一场名为"Wonderlust"的特别活动。
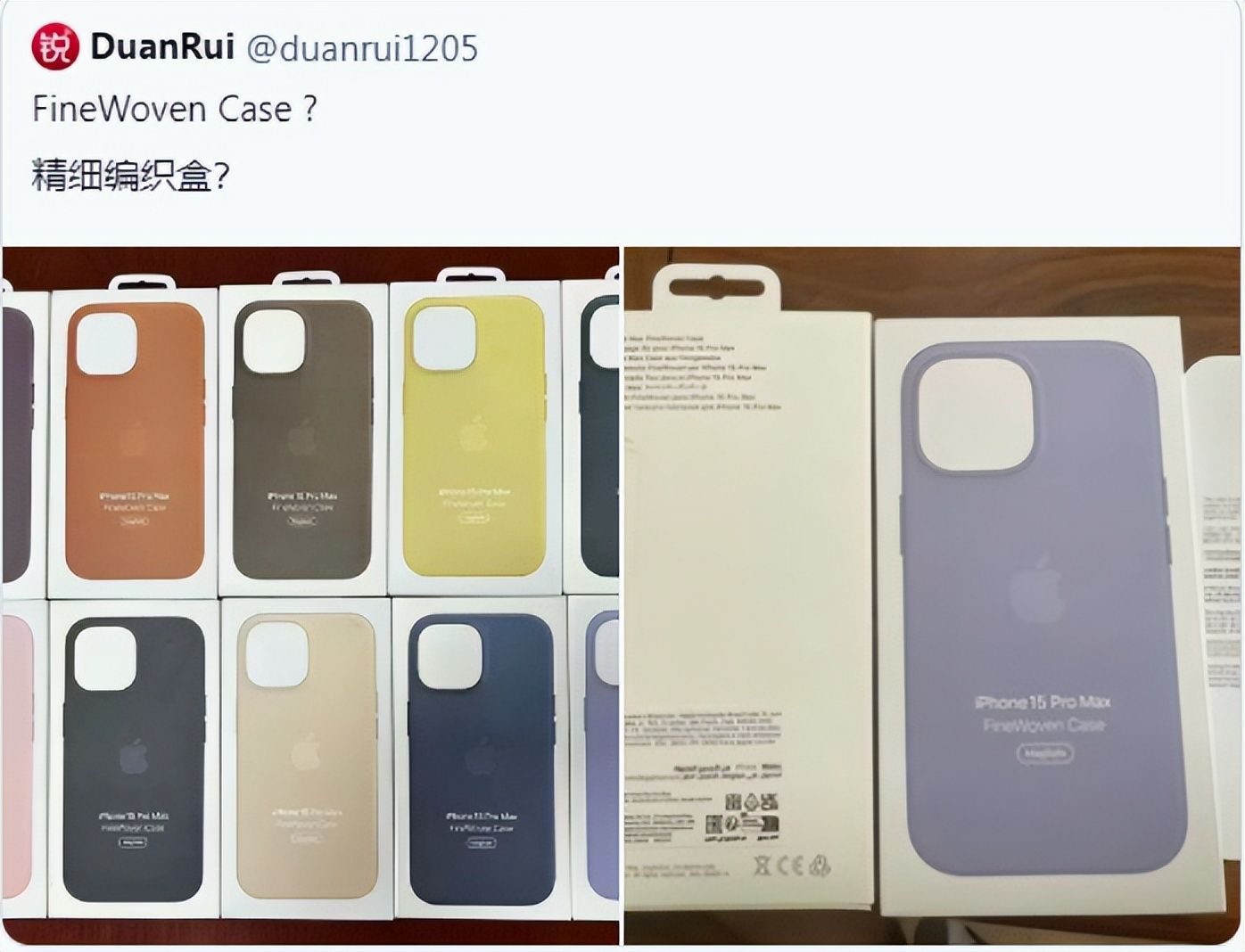
届时,预计将正式发布iPhone 15、iPhone 15 Plus、iPhone 15 Pro、iPhone 15 Pro Max、Apple Watch Series 9、第二代Apple Watch Ultra以及一系列新配件。此次发布会将为苹果粉丝和消费者展示最新的创新技术和设计,其中包括USB-C AirPods Pro MagSafe充电盒、"FineWoven"手机壳和一款新的Apple Watch表带等。

这次的发布会将进一步拓展用户对iPhone 15系列和Apple Watch Series 9的期待,并且提供了更多选择和个性化定制的可能性。无论是材料的创新还是配件的新发展,苹果都致力于提供出色的产品和服务,满足广大用户的需求。