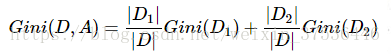给你一个整数数组 nums,请你将该数组升序排列。
示例 1:
输入:nums = [5,2,3,1] 输出:[1,2,3,5]
示例 2:
输入:nums = [5,1,1,2,0,0] 输出:[0,0,1,1,2,5]
代码如下:
1.插入排序(简单插入排序、直接插入排序)
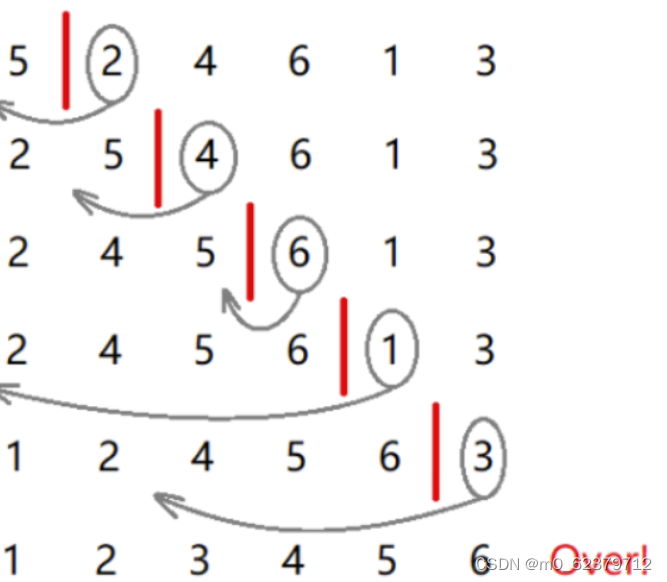
//算法思想;从当前位置开始,从后往前找比数字小的,找到后插入到这个小的数字后面
//再找的过程中,如果发现一个比当前数字大,同时将这个数字往后移动
//时间复杂度:O(n^2) 空间复杂度O(1) 稳定性:稳定,没有跳跃式的交换数据
//直接插入排序的特点:越有序越快;完全有序能达到O(n);
class Solution {
public:
void InsertSort(vector<int>& nums,int n)
{
for(int i=0;i<n;i++)
{
int temp = nums[i];//记录未排序数组的下标
int j = i-1;//记录已经排序数组的下标
while(j >= 0 && nums[j] >temp)
{
nums[j+1] = nums[j];//当已经排序好的数组数字大于未排序的数组数字,将已经排序好的数字向后移一个
j--;
}
nums[j+1] = temp;//如果未排序的数组数字大于已经排序好的数字,直接插入到排序好的数字后面
}
}
vector<int> sortArray(vector<int>& nums) {
int n=nums.size();
InsertSort(nums,n);
return nums;
}
};2.希尔排序
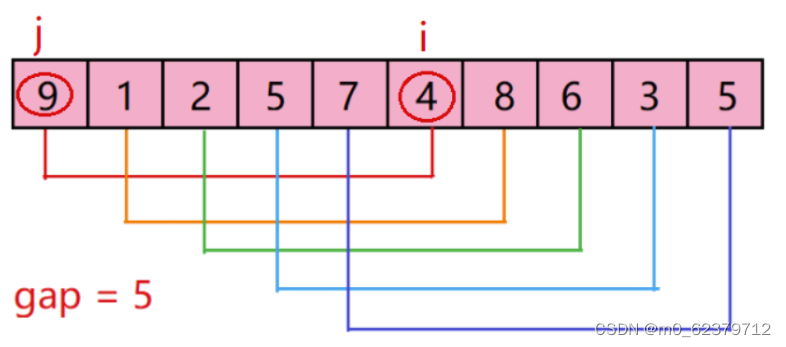
//直接插入排序越有序越快是希尔排序的一个理论基础
//算法描述:1.间隔式的分组 2.利用直接插入排序让组内有序 3.缩小分组再次排序 4.再次调用直接插入排序 ...直到缩为一组完全有序
//时间复杂度:O(n^1.3-n^1.5) 空间复杂度:O(1) 稳定性:不稳定
class Solution {
public:
void ShellSort(vector<int>& nums,int n)
{
int gap=n;
while(gap>1)//间隔式分组,每一组利用直接插入排序,让组内有序
{
gap/=2;//每次分组都在上一组的基础上折半
for(int i=gap;i<n;i++)
{
int temp = nums[i];
int j = i-gap;
while(j >= 0 && nums[j] >temp)
{
nums[j+gap] = nums[j];
j-=gap;
}
nums[j+gap] = temp;
}
}
}
vector<int> sortArray(vector<int>& nums) {
int n=nums.size();
ShellSort(nums,n);
return nums;
}
};3.冒泡排序
代码如下:
//两两比较,大的往后走
//时间复杂度:O(n^2) 空间复杂度:O(1) 稳定性:稳定
class Solution {
public:
void BubbleSort(vector<int>& nums,int n)
{
for(int i=0;i<n-1;i++)//走的趟数
{
for(int j=0;j<n-i-1;j++)//每走一遍,最大的数字在最后面,走的次数越多,越往后面的数字排序越正确
{
if(nums[j]>nums[j+1])//两两交换,较大的数字在后面
{
int temp=nums[j];
nums[j]=nums[j+1];
nums[j+1]=temp;
}
}
}
}
vector<int> sortArray(vector<int>& nums) {
int n=nums.size();
BubbleSort(nums,n);
return nums;
}
};4.快速排序
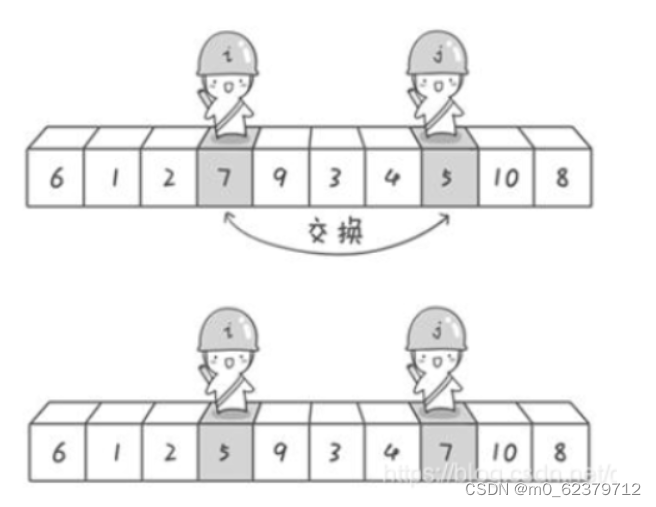
代码如下:
//算法描述:先在数据中找到一个基准,从后往前找比基准小的数字,找到后往前挪动
//从前往后找比基准大的数字,找到往后挪动 重复之前的动作
//一次划分的时间复杂度:O(n) 划分logn次
//时间复杂度:O(nlogn) 空间复杂度:O(logn)(递归的次数)
//快排的缺点:空间复杂度大,不稳定
//快排最大缺点:越有序越慢,完全有序,为O(n^2)退化为选择排序
class Solution {
public:
void QuickSort(vector<int>& nums,int left,int right)
{
if(left>=right)//只有一个数或区间不存在
{
return;
}
int i=left,j=right;//i在最左边,j在最右边
int base=nums[left];//定义最左边的数字为基准
while(i<j)
{
while(nums[j]>=base&&i<j)//从后往前找比这个比准数字小的
{
j--;
}
while(nums[i]<=base&&i<j)//从前往后找比这个基准数字大的
{
i++;
}
swap(nums[i],nums[j]);//找到之后交换两个数字
}
nums[left]=nums[i];//当i=j时,将基准数字与nums[i]交换
nums[i]=base;
//在一次完成之后,左边的数字都比基准数字小,右边的数字都比基准数字大
QuickSort(nums,left,i-1);//递归左边
QuickSort(nums,i+1,right);//递归右边
}
vector<int> sortArray(vector<int>& nums) {
int n=nums.size();
QuickSort(nums,0,n-1);
return nums;
}
};5.选择排序
代码如下:
//算法描述:每次都从待排序中找到最小值和待排序的第一个交换
//时间复杂度:O(n^2) 空间复杂度:O(1) 稳定性:不稳定
class Solution {
public:
void SelectSort(vector<int>& nums,int n)
{
int minIndex;
for(int i=0;i<n-1;i++)
{
minIndex=i;
for(int j=i+1;j<n;j++)
{
if(nums[minIndex]>nums[j])
{
minIndex=j;
}
}
swap(nums[i],nums[minIndex]);
}
}
vector<int> sortArray(vector<int>& nums) {
int n=nums.size();
SelectSort(nums,n);
return nums;
}
};