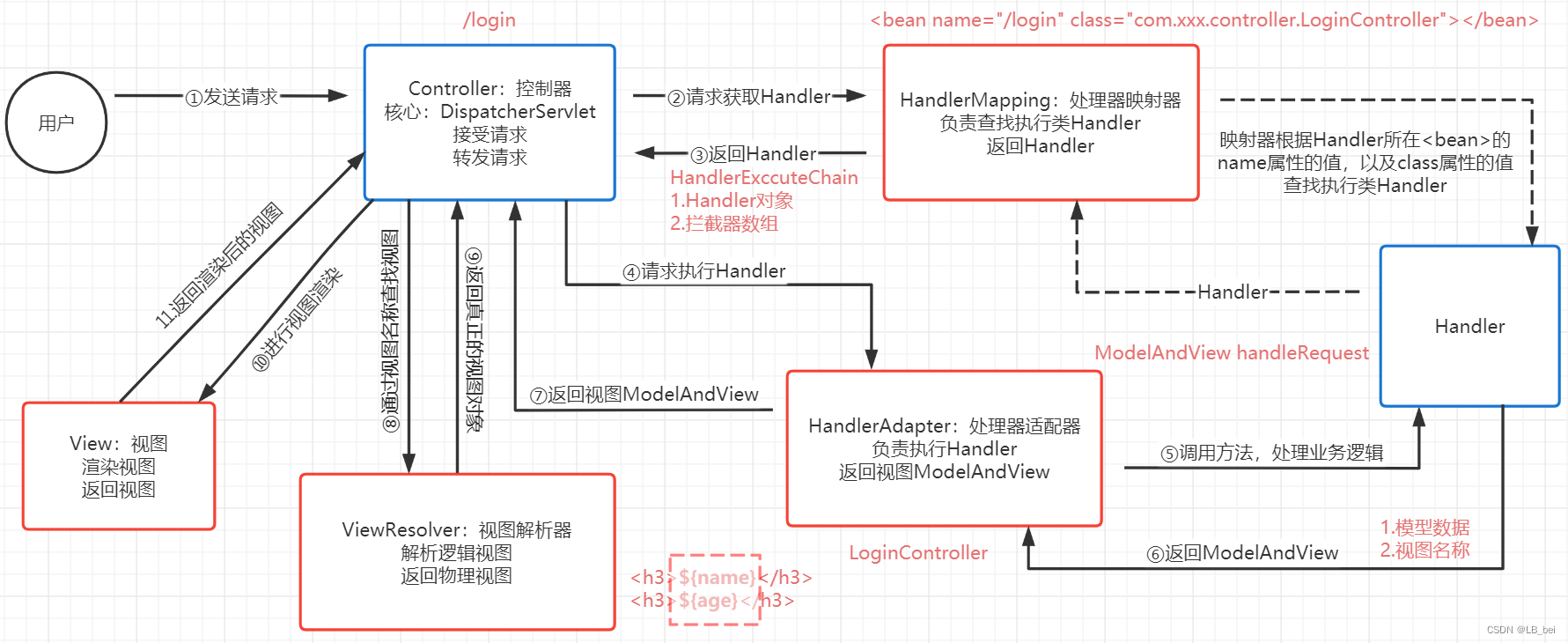
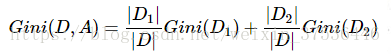IIC(Inter-Integrated Circuit)是一种两线式串行总线协议,用于连接微控制器及其他外围设备。在IIC总线上的数据传输速率可以是标准模式(100Kbit/s),快速模式(400Kbit/s)和高速模式(3.4Mbit/s)。
IIC的起始和停止条件由SCL(Serial Clock Line,串行时钟线)和SDA(Serial Data Line,串行数据线)的状态决定。起始条件是当SCL为高电平时,SDA由高电平向低电平跳变;停止条件是当SCL为高电平时,SDA由低电平向高电平跳变。在空闲状态下,SCL和SDA都处于高电平。
IIC的应答机制是一种相互关系,当主机发送数据给从机时,从机必须在接收到每个字节后向主机发送一个应答信号,表示已收到数据。应答信号是一个位宽为9个时钟周期的脉冲信号,其中第9个时钟周期是高电平。如果从机没有接收到数据或者无法应答,则在第9个时钟周期保持低电平。
协议波形如下图
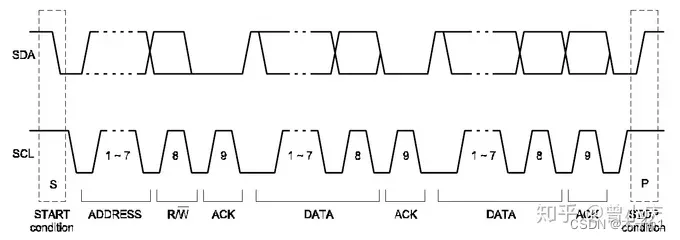
在数据传输过程中,主机在SCL的每个高电平周期开始时发送一个位宽为8位的字节,然后等待从机的应答信号。从机在接收到每个字节后,在第9个时钟周期发送一个应答信号。主机可以重复发送数据,直到从机发送非应答信号或者停止条件被触发。
IIC波形表示了主机和从机之间的数据传输过程和应答机制。起始和停止条件以及应答机制都是IIC通信的基本要素。