Python实现马尔科夫链预测
马尔科夫链原理
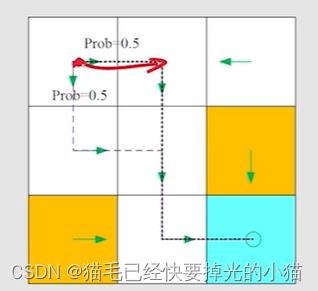
马尔科夫链是一种进行预测的方法,常用于系统未来时刻情况只和现在有关,而与过去无关。
用下面这个例子来讲述马尔科夫链。

如何预测下一时刻计算机发生故障的概率?
当前状态只存在0(故障状态)和1(正常状态)两种,每种状态下各存在两个未来状态(00,01,11,10),那么统计出这整个序列中00,01,11,10出现的次数。即求得转移矩阵。

进而求得转移概率矩阵

如果当前是0,那么下一个是0的概率为30.77%,下一步为1的概率为69.23%。
对当前数据,最后一个为1,那么预测下一步,有74.3%的概率不发生故障。
上面的方法不仅限于两个类别0和1,多类别也是可以预测的
比如

str = “4321431123212344331113321222442323112431”
用同样的方法计算转移概率矩阵
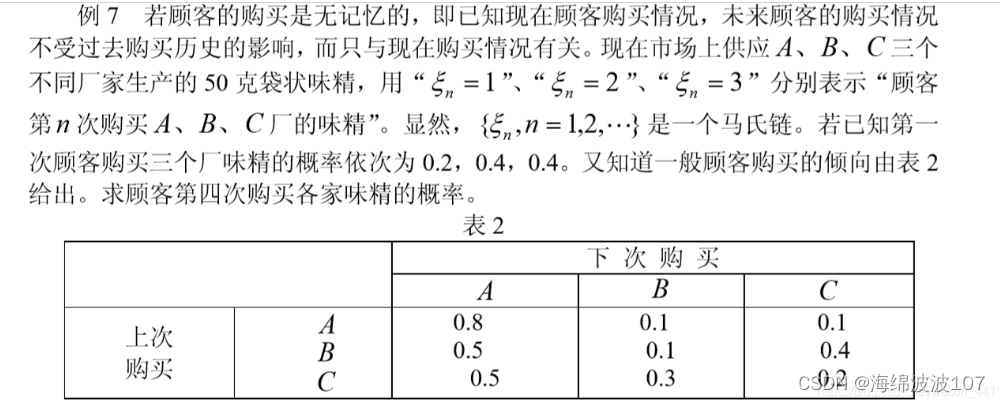
问题描述
源代码
计算转移矩阵部分
def str_count(str, sub):
count = 0
for i in range(0, len(str) - 1):
if str[i:i+2] == sub:
count = count + 1
return count
def data_to_matrix():
str = "1110010011111110011110111111001111111110001101101111011011010111101110111101111110011011111100111"
count00 = str_count(str, "00")
count01 = str_count(str, "01")
count10 = str_count(str, "10")
count11 = str_count(str, "11")
print("count00:", count00)
print("count01:", count01)
print("count10:", count10)
print("count11:", count11)
if __name__ == '__main__':
data_to_matrix()
问题解决部分
import numpy as np
p1 = np.array([0.2, 0.4, 0.4])
p = np.array([
[0.8, 0.1, 0.1],
[0.5, 0.1, 0.4],
[0.5, 0.3,0.2]
])
p3 = np.linalg.matrix_power(p, 3)
p4 = np.dot(p1, p3)
print(p4)
1、np.linalg.matrix_power(p, 3) 是一个用来计算矩阵 p 的 3 次幂的函数。它使用 NumPy 库中的 linalg 子模块来执行矩阵乘法运算。这个函数的返回值是将矩阵 p 自乘 3 次后得到的新矩阵。
2、dot指的是两个向量之间的点积运算
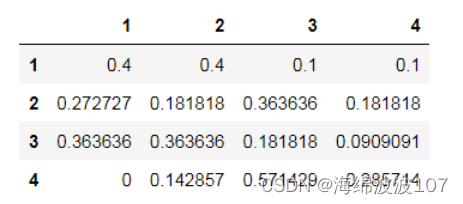
结果


参考博文
数学建模入门-python实现简单的马尔可夫链
马尔科夫链预测,Python实现