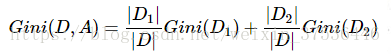一、决策树简介
首先决策树是一种有监督的机器学习算法,其采用的方法是自顶向下的递归方法,构建一颗树状结构的树,其具有分类和预测功能。其基本思想是以信息熵为度量构造一棵熵值下降最快的树,到叶子节点处的熵值为零。决策树的构建通常分为三个步骤:
1、特征选择
特征选择就是要选取具有较强分类能力的特征,分类能力通过信息增益或信息增益率来进行刻画。选择的标准是找出局部最优的特征作为判断进行切分,取决于切分后节点数据集合中类别的有序程度。衡量节点的数据集合的纯度有:信息增益(率)、基尼系数和方差(方差主要是针对回归的)。
2、决策树的生成
在决策树的生成算法中,常规的算法有ID3和C4.5生成算法。两者生成的过程类似,区别在于前者采用信息增益作为特征的度量,而后者采用信息增益率。但ID3和C4.5存在某些不足,因此改进的CART算法便产生了,它是采用基尼系数作为度量属性的选择。
3、决策树剪枝
决策树需要剪枝的原因是:决策树的生成算法生成的树对训练数据的预测很准确,但是对于未知的数据分类能力却很差,容易产生过拟合的现象。剪枝的过程是从已经生成的决策树上剪掉一些子树或者叶子节点。剪枝的目标是通过极小化决策树的整体损失函数或代价函数实现,其目的是提高模型的泛化能力。
二、决策树的生成算法
主要有ID3、C4.5和CART树算法。
首先来介绍ID3算法:
其思路是用信息增益的大小来判断当前节点应该用什么特征来构建决策树,用计算出的信息增益最大的特征来建立决策树的当前节点。
特征A对训练数据集D的信息增益g(D,A),定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差,即:
g(D,A)=H(D) – H(D|A)
其中H(D)度量了D的不确定性,H(D|A)度量了D在知道了A以后D剩下的不确定性,两者之差则度量了D在知道了A以后不确定性的减少程度。
ID3算法的不足:
1、其没有考虑连续特征,比如长度,密度都是连续值
2、其采用的信息增益大的特征优先建立决策树的节点。这就导致了在相同条件下取值较多的特征比取值较少的特征的信息增益 大。,例如一个变量有两个值,都为1/2,另一个变量有三个值,都为1/3,由于他们都是完全不确定的变量,但是取3个值的比取2个值的信息增益大。
3、ID3算法没有对于缺失值的情况做考虑。
4、ID3算法没有考虑过拟合的问题。
其次是C4.5算法
对于ID3算法存在的问题,C4.5对其做了进一步的改进。
首先对于不能处理连续特征的问题,C4.5的思路是将连续的特征离散化。比如m个样本的连续特征A有m个,从小到大排列为a1,a2...,am,则C4.5取相邻两样本值的平均数,一共取得m-1个划分点,其中第i个划分点Ti表示为:Ti=(ai+a(i+1))/2。对于这m-1个点,分别计算该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为at,则小于at的值为类别1,大于为类别2,这样就做到连续特征的离散化处理。
其次对于信息增益作为标准容易偏向于取值较多的特征的问题。引入了信息增益率作为度量特征的选择,它是信息增益和特征熵的比值。表达式如下:
Gr(D,A) = g(D,A) / HA(D)
信息熵g(D,A),H(A)为特征熵,对于H(A)其表达式如下:
其中n为特征A的类别数,Di为特征A的第i个取值对应的样本个数。D为样本个数。
再者,对于缺失值的问题,主要解决的问题主要有两个,一是在样本某些特征缺失的情况下选择划分的属性,二是选定了划分属性,对于在该属性上缺失特征的样本处理。
最后,对于过拟合的问题,C4.5引入了正则化系数进行初步的剪枝。
C4.5算法的不足:
1、C4.5剪枝的算法存在优化的空间。
2、C4.5算法生成的是多叉树,即一个父节点可以有多个节点。
3、C4.5只能用于分类
4、C4.5由于使用了熵模型,里面有大量的耗时的对数运算。
下面介绍CART算法:
CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益是相反的。
在分类问题中,假设有K个类别,第k个类别的概率为pk,则基尼系数的表达为:
如果是二分类为题,计算就更加简单,如果属于第一个样本输出的概率为p,则基尼系数的表达式为:
Gini(p)=2p(1-p)
对于给定的样本D,假设有K个类别,第k个类别的数量为Ck,则样本D的基尼系数表达式为:
Gini(D)=1-∑(|Ck|/|D|)^2特别地,对于样本D,如果根据特征A的某个值a,把D分为D1和D2两部分,则在特征A的条件下,D的基尼系数表达式为:
三、决策树CART算法的剪枝
目的:
对于没有进行剪枝的树,就是一个完全生长的决策树,是过拟合的,因此需要去掉一些不必要的节点以以提高训练出的决策树模型的泛化能力。
决策树算法剪枝的过程是由两个过程组成:
1、从T0开始不断的剪枝,直到剪成一颗单节点的树,这些剪枝树形成一个剪枝树序列{T0,T1,T2...,Tn}。
2、从上面形成的剪枝序列中挑选出最优剪枝树。方法是:通过交叉验证法使用验证数据集对剪枝树序列进行测试。
首先,给出决策树算法的损失函数:
Cα(T)=C(T)+α|T| 其中C(T)为决策树对训练数据的预测误差:|T|为决策树的叶子节点数对固定的α,存在使Cα(T)最小的树,令其为Tα,可以证明Tα是唯一的。
当α大时,Tα偏小(即决策树比较简单)
当α小时,Tα偏大(即决策树比较复杂)
当α=0时,生成的决策树就是最优的
当α为无穷时,根组成的一个单节点树就是最优的。
考虑生成树T0.对T0内的任意节点t,以t为单节点树(记作t')的损失函数为:Cα(t')=C(t')+α,以t为根的子树Tt的损失函数为:
Cα(Tt)=C(Tt)+α|Tt|。可以证明:
当α=0及充分小时,有Cα(Tt)<Cα(t')
当α增大到某个值时,有Cα(Tt)=Cα(t')
当α再增大时时,有Cα(Tt)>Cα(t')
因此令α=(C(t'<C(Tt)))/(|Tt|-1),此时t'与Tt有相同的损失函数值,但是t'的叶节点更少,于是对Tt进行减值成一颗单节点树t'了。
对T0内部的每一个节点t,定义g(t)=(C(t'<C(Tt)))/(|Tt|-1)。设T0内g(t)最小的子树为Tt*,令该最小值的g(t)为α1'。从T0中剪去Tt*,即得到剪枝树T1,重复这种“求g(t)-剪枝”过程,直到根节点即完成剪枝。在此过程中不断增加αi'的值,从而生成剪枝树序列。
CART剪枝交叉验证过程是通过验证数据集测试剪枝树序列{T0,T1,T2...,Tn}中个剪枝树的。对于CART回归树,是考察剪枝树的平方误差,平方误差最小的决策树被认为是最有决策树。对于CART分类树,是考察基尼指数,基尼指数最小的决策树被认为是最优的决策树。
四、决策树代码实例
下面是一个使用Python的scikit-learn库实现决策树的代码示例
# 导入所需的库
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
# 加载数据集
iris = load_iris()
X = iris.data # 特征向量
y = iris.target # 目标变量
# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)
# 创建决策树分类器
clf = DecisionTreeClassifier(max_depth=3, random_state=1)
# 训练决策树模型
clf.fit(X_train, y_train)
# 使用训练好的模型进行预测
y_pred = clf.predict(X_test)
# 计算准确率
accuracy = metrics.accuracy_score(y_test, y_pred)
print("准确率:", accuracy)
# 可视化决策树
plt.figure(figsize=(10, 6))
plot_tree(clf, filled=True, rounded=True, feature_names=iris.feature_names, class_names=iris.target_names)
plt.show() 以上代码实现了对鸢尾花数据集的分类任务。首先,导入所需的库。然后,加载鸢尾花数据集,其中X是特征向量,y是目标变量。接着,将数据集划分为训练集和测试集,其中测试集占总数据集的30%。然后,创建一个决策树分类器,并指定最大深度为3和随机种子为1。
在决策树模型中,设置最大深度可以控制决策树的复杂度,避免过拟合。较小的最大深度可以降低模型的复杂度,但也可能导致欠拟合。随机种子用于重现结果,确保每次运行代码时得到相同的结果。
接着,使用训练集对决策树模型进行训练。然后,使用训练好的模型对测试集进行预测并得到预测结果y_pred。
使用metrics.accuracy_score函数计算预测准确率,并将结果打印出来。
最后,使用matplotlib库将决策树可视化显示出来。通过调用plot_tree函数并传入决策树模型、特征名和目标类别名等参数,可以生成决策树的图形化显示。