目录

1.算法流程简介

2.算法核心代码

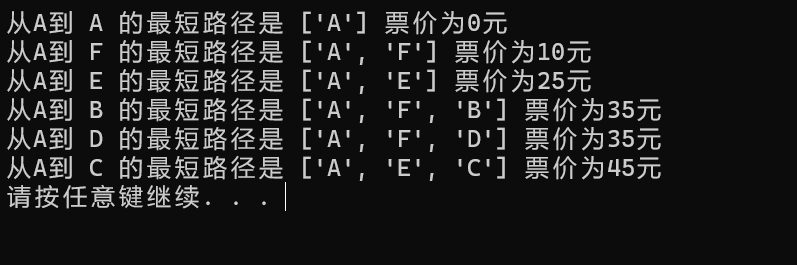
3.算法效果展示

1.算法流程简介

#最短路径算法
#针对有向图的最短路径问题,我们有很多的算法能解决.
"""
目前主流算法如下所示:
Dijkstra算法:Dijkstra算法是一种单源最短路径算法,用于计算从起点到其它所有节点的最短路径。该算法的基本思想是从起点开始，依次计算每个节点到起点的最短路径，然后再依次计算每个节点到起点的最短路径，直到所有节点都被计算完毕。。
Ford算法:Ford算法是一种动态规划算法,用于找到带权重的有向图中从一个起点到所有其他节点的最短路径。该算法可以处理负边权图，并且还可以检测到负权环。
Floyd-Warshall算法:Floyd-Warshall算法是一种动态规划算法,用于找到带权重的有向图中任意两个节点之间的最短路径。该算法可以处理负边权图，并且可以同时计算多组最短路径。
"""
"""
#在python中,我们能够借用networkx库中的函数来进行最短路径的求解
如下所示:networks_shortest_path(G,source,target,weight,method)函数如下所示:
networkx.shortest_path(G, source=None, target=None, weight=None, method='dijkstra')
1.G代表图矩阵,可以是无向或者有向
2.source代表的是起始点
3.target代表的是终止点
4.weight代表的边与边之间的权重关系
5.method表示所用的算法,默认为Dijkstra,也可以指定Bellman-Ford和Floyd-Warshall。
#ps1:该算法返回值是一个字典,键表示的是目标结点,值表示最短路径
#ps2:如果需要求最短的距离,请使用networks_short_path_length()
"""
具体流程步骤:
#1.导入各边距离权重矩阵
#2.将矩阵进行转化
#3.求解任意点的最短路径问题,以A点为例

2.算法核心代码

import networkx as nx
#1.导入各边距离权重矩阵
number=6#gragh中参与计算的点的数量
dis = [[0, 50, 0, 40, 25, 10],
         [50, 0, 15, 20, 0, 25],
         [0, 15, 0, 10, 20, 0],
         [40, 20, 10, 0, 10, 25],
         [25, 0, 20, 10, 0, 55],
         [10, 25, 0, 25, 55, 0]]
#2.将矩阵进行转化
G=nx.DiGraph()
for i in range(number):
    for j in range(number):
        if dis[i][j]!=0:#可以处理负权
            G.add_edge(chr(i+65),chr(j+65),weight=dis[i][j])
#3.求解任意点的最短路径问题,以A点为例
best_path = nx.shortest_path(G, source='A', weight='weight') 
best_path_length = nx.shortest_path_length(G, source='A', weight='weight')#答案存在这里   
for loc,cost in best_path_length.items():
    print("从A到",str(loc),"的最短路径是",str(best_path[loc]),"票价为"+str(cost)+"元")

3.算法效果展示