目录
1.算法设计思路
2.算法核心代码
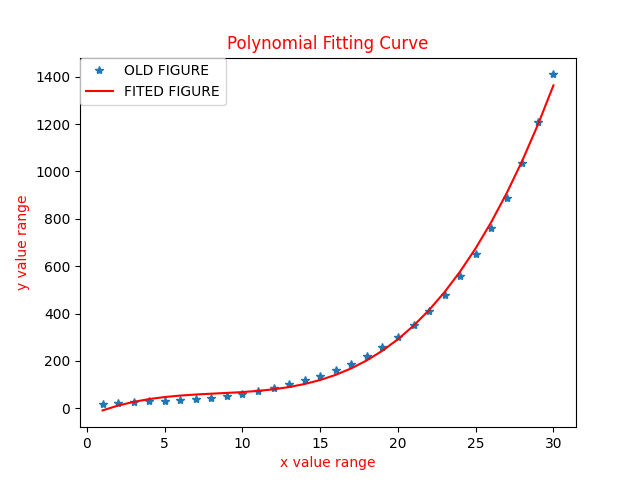
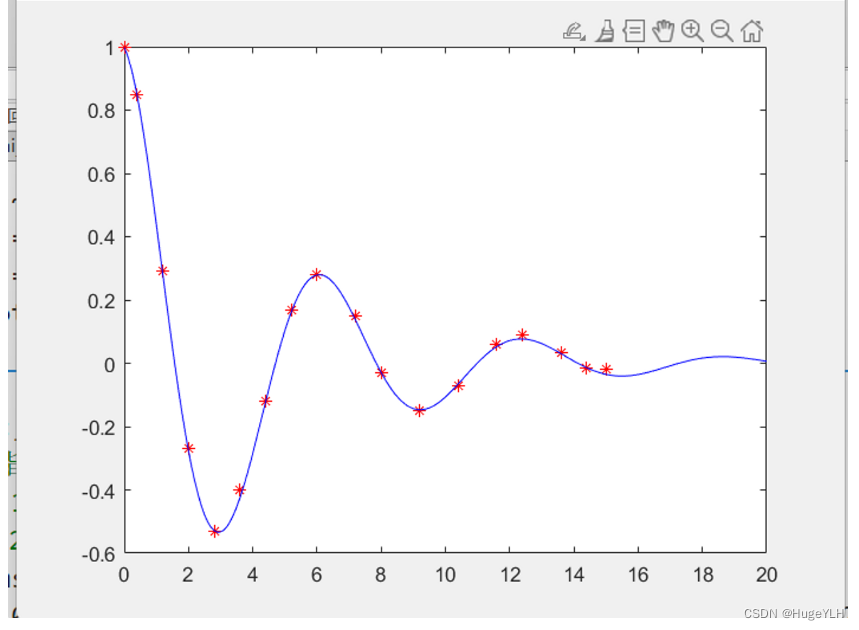
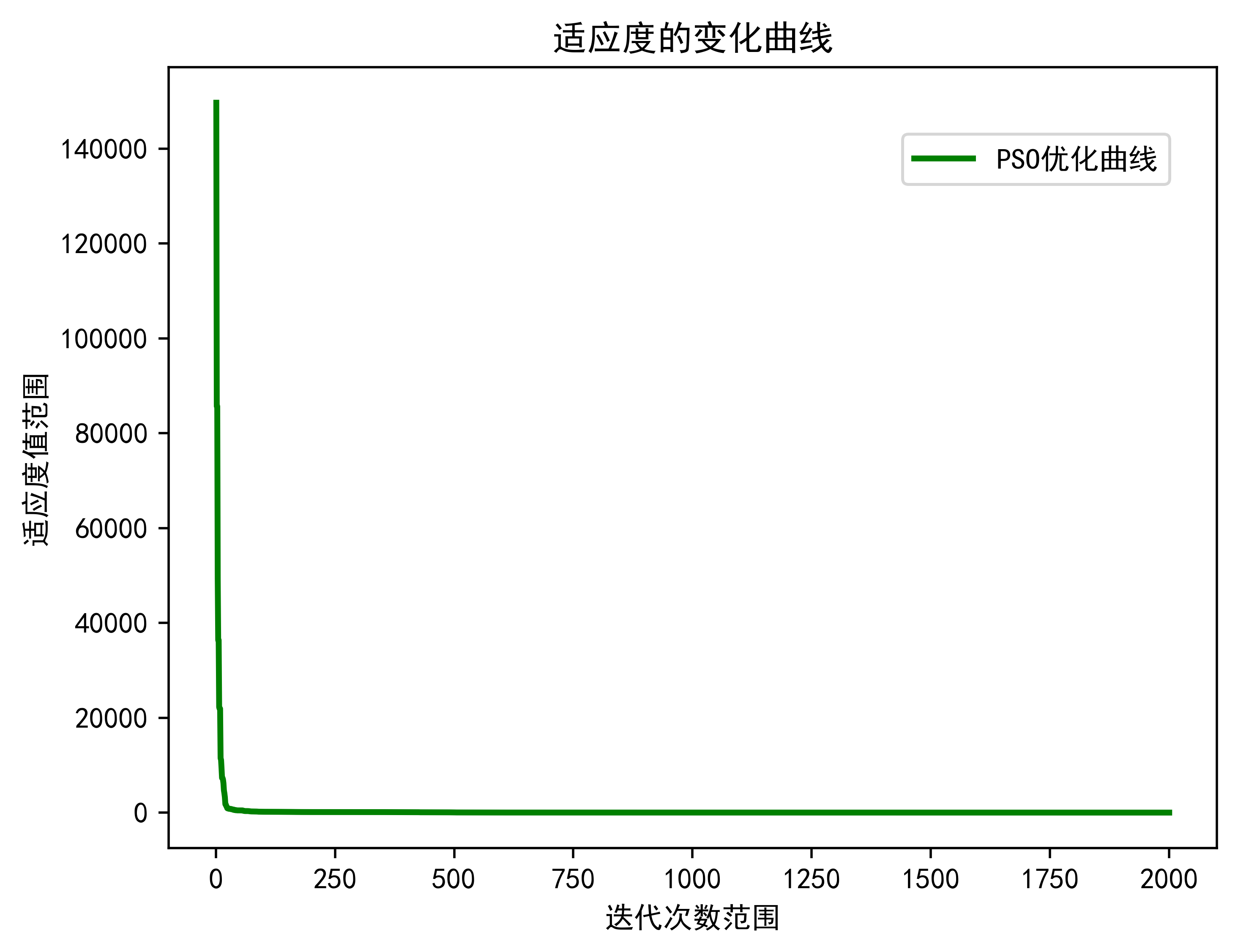
3.算法效果展示
1.算法设计思路
算法关键步骤:(主要是利用到多项式拟合的库包)
1.将数据进行导入
2.进行曲线拟合返回值为各项系数
3.获得多项式拟合之后的函数表达式
4.将x代入表达式求出对应的y值(这样就能够表示出拟合的差别如何)
5.进行可视化绘图2.算法核心代码
#def poly_fit_deal(x,y,degree,rcond=None,full=False,w=None,cov=False)
#导入一些库和函数
import pylab as plb
import numpy as np
import matplotlib.pyplot as plt
#1.将数据进行输入
x = np.arange(1, 31, 1)
y = np.array([20, 23, 26, 29, 32, 35, 38, 45, 53, 62, 73, 86, 101, 118, 138, 161, 188, 220, 257,
300, 350, 409, 478, 558, 651, 760, 887, 1035, 1208, 1410])
#2.进行曲线拟合返回值为各项系数
first_step=np.polyfit(x,y,3)
#3.获得多项式拟合之后的函数表达式
p1=np.poly1d(first_step)
#4.将x代入表达式求出对应的y值(这样就能够表示出拟合的差别如何)
y_new=p1(x)
#5.进行可视化绘图
plb.title('Polynomial Fitting Curve',color='r')
plb.xlabel('x value range',color='r')
plb.ylabel('y value range',color='r')
fig1=plb.plot(x,y,'*',label='OLD FIGURE')
fig2=plb.plot(x,y_new,'r',label='FITED FIGURE')
plb.legend(loc=3, borderaxespad=0., bbox_to_anchor=(0, 0.873))
plt.show()3.算法效果展示