参考文章
Ubuntu Linux 与主机共享文件夹
vim 修改文件出现错误 “ E45: ‘readonly’ option is set (add to override)“
vim退出时报错“E212: Can't open file for writing”的解决办法
VMware 安装后,安装Ubuntu 20.04一路顺利。
1,在VMware设置共享后,需要在ubuntu能够访问到,共享设置如下:
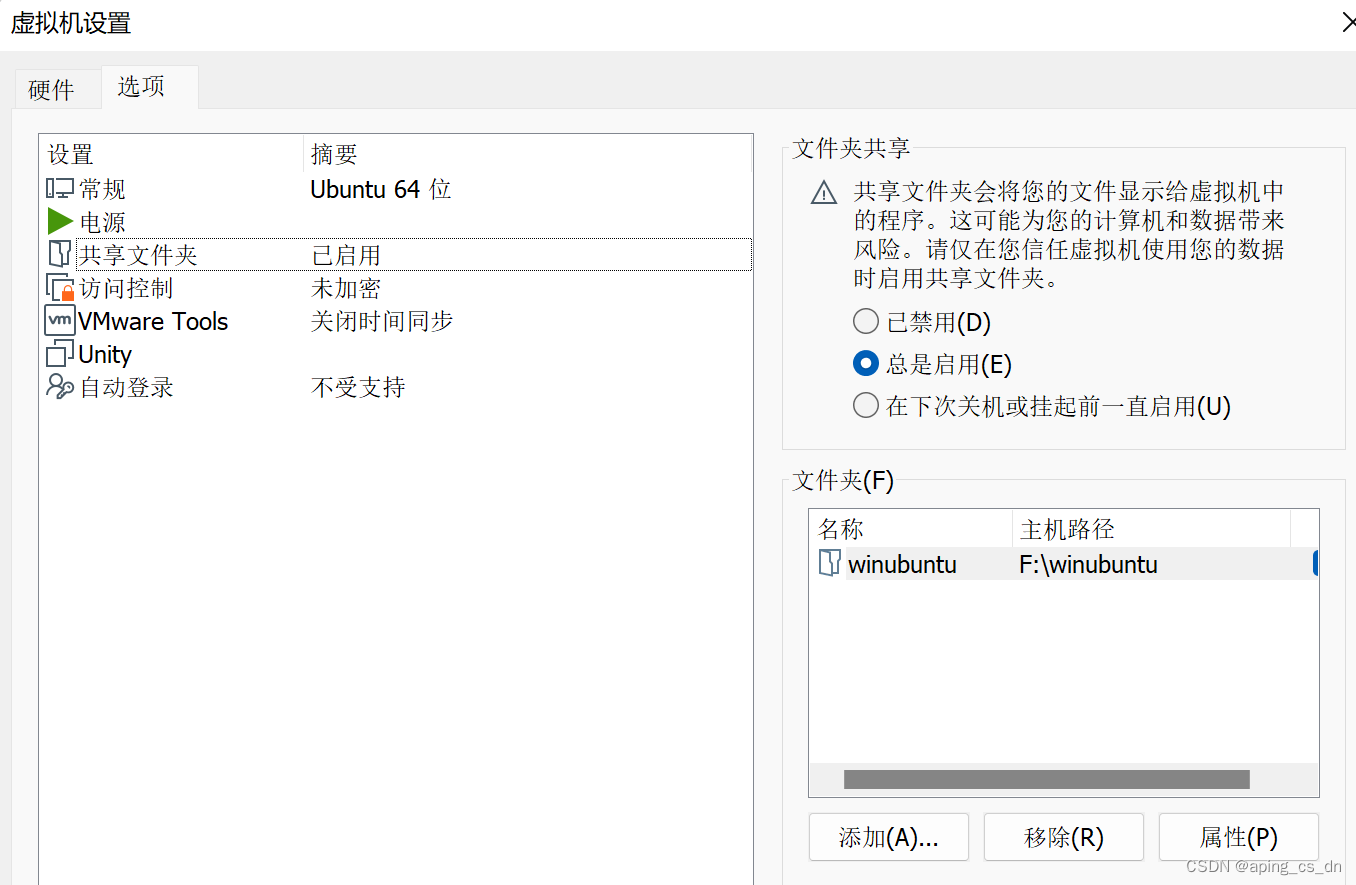
2,在Ubuntu中查看
aping@ubuntu:~/Desktop$ vmware-hgfsclient
winubuntu
3,执行如下命令创建共享文件夹专用的挂载目录。(无反应的,正常。该指令执行一次,以后重新开机不再需要再次输入,该挂载目录已经创建成功。)
aping@ubuntu:~/Desktop$ sudo mkdir -p /mnt/hgfs
[sudo] password for aping:
4,执行以下命令挂载共享文件夹(该命令每次开机都要执行,重新挂载。)
ping@ubuntu:~/Desktop$ sudo /usr/bin/vmhgfs-fuse .host:/ /mnt/hgfs -o subtype=vmhgfs-fuse,allow_other
aping@ubuntu:~/Desktop$ ls -l /mnt/hgfs
total 0
drwxrwxrwx 1 root root 0 Sep 3 17:37 winubuntu
5, 要在开机时自动挂载共享文件夹,则需要更改/etc/fstab文件,在该文件添加以下语句即可。
.host:/ /mnt/hgfs fuse.vmhgfs-fuse allow_other.defaults 0 06,因为要修改fstab文件,需要使用vim,如果系统没有安装,则提示安装:
aping@ubuntu:~/Desktop$ vim /etc/fstab
Command 'vim' not found, but can be installed with:
sudo apt install vim # version 2:8.1.2269-1ubuntu5.17, or
sudo apt install vim-tiny # version 2:8.1.2269-1ubuntu5.17
sudo apt install vim-athena # version 2:8.1.2269-1ubuntu5.17
sudo apt install vim-gtk3 # version 2:8.1.2269-1ubuntu5.17
sudo apt install vim-nox # version 2:8.1.2269-1ubuntu5.17
sudo apt install neovim # version 0.4.3-3
aping@ubuntu:~/Desktop$ sudo apt install vim
7,安装后 继续执行vim,打开fstab文件,加入底5步的配置语句,如下
# /etc/fstab: static file system information.
#
# Use 'blkid' to print the universally unique identifier for a
# device; this may be used with UUID= as a more robust way to name devices
# that works even if disks are added and removed. See fstab(5).
#
# <file system> <mount point> <type> <options> <dump> <pass>
# / was on /dev/sda5 during installation
UUID=d6371bca-30db-401b-a1bf-3ced69503245 / ext4 errors=remount-ro 0 1
# /boot/efi was on /dev/sda1 during installation
UUID=DDEB-E353 /boot/efi vfat umask=0077 0 1
/swapfile none swap sw 0 0
/dev/fd0 /media/floppy0 auto rw,user,noauto,exec,utf8 0 0
.host:/ /mnt/hgfs fuse.vmhgfs-fuse allow_other.defaults 0 0
8,因为文件是只读权限, 需要通过如下方式提升权限:
:w !sudo tee %之后再退出便具有super权限了。