【码极客精讲】桶排序

桶排序 (Bucket sort)或所谓的箱排序，是一个排序算法，工作的原理是将数组分到有限数量的桶子里。每个桶子再个别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序）。桶排序是鸽巢排序的一种归纳结果。当要被排序的数组内的数值是均匀分配的时候，桶排序使用线性时间（Θ（n））。但桶排序并不是比较排序，他不受到 O(n log n) 下限的影响。4

定义

假定：输入是由一个随机过程产生的[0, 1)区间上均匀分布的实数。将区间[0, 1)划分为n个大小相等的子区间（桶），每桶大小1/n：[0, 1/n)， [1/n, 2/n)， [2/n, 3/n)，…，[k/n, (k+1)/n )，…将n个输入元素分配到这些桶中，对桶中元素进行排序，然后依次连接桶输入0 ≤A[1..n] <1辅助数组B[0..n-1]是一指针数组，指向桶（链表）。

算法

桶排序算法要求，数据的长度必须完全一样，程序过程要产生长度相同的数据，使用下面的方法：Data=rand()/10000+10000上面提到的，每次下一次的扫描顺序是按照上次扫描的结果来的，所以设计上提供相同的两个桶数据结构。前一个保存每一次扫描的结果供下次调用，另外一个临时拷贝前一次扫描的结果提供给前一个调用。

数据结构设计：链表可以采用很多种方式实现，通常的方法是动态申请内存建立结点，但是针对这个算法，桶里面的链表结果每次扫描后都不同，就有很多链表的分离和重建。如果使用动态分配内存，则由于指针的使用，安全性低。所以，笔者设计时使用了数组来模拟链表（当然牺牲了部分的空间，但是操作却是简单了很多，稳定性也大大提高了）。共十个桶，所以建立一个二维数组，行向量的下标0—9代表了10个桶，每个行形成的一维数组则是桶的空间。

平均情况下桶排序以线性时间运行。像基数排序一样，桶排序也对输入作了某种假设，因而运行得很快。具体来说，基数排序假设输入是由一个小范围内的整数构成，而桶排序则假设输入由一个随机过程产生，该过程将元素一致地分布在区间[0，1)上。桶排序的思想就是把区间[0，1)划分成n个相同大小的子区间，或称桶，然后将n个输入数分布到各个桶中去。因为输入数均匀分布在[0，1)上，所以一般不会有很多数落在一个桶中的情况。为得到结果，先对各个桶中的数进行排序，然后按次序把各桶中的元素列出来即可。

在桶排序算法的代码中，假设输入是含n个元素的数组A，且每个元素满足0≤ A[i]<1。另外还需要一个辅助数组B[O..n-1]来存放链表实现的桶，并假设可以用某种机制来维护这些表。

桶排序的算法如下(伪代码表示)，其中floor(x)是地板函数，表示不超过x的最大整数。

procedure Bin_Sort(var A:List);begin

n:=length(A);

for i:=1 to n do

将A[i]插到表B[floor(n*A[i])]中;

for i:=0 to n-1 do

用插入排序对表B[i]进行排序;

将表B[0],B[1],...,B[n-1]按顺序合并;

end;

右图演示了桶排序作用于有10个数的输入数组上的操作过程。(a)输入数组A[1..10]。(b)在该算法的第5行后的有序表(桶)数组B[0..9]。桶i中存放了区间[i/10，(i+1)/10]上的值。排序输出由表B[O]、B[1]、...、B[9]的按序并置构成。

要说明这个算法能正确地工作，看两个元素A[i]和A[j]。如果它们落在同一个桶中，则它们在输出序列中有着正确的相对次序，因为它们所在的桶是采用插入排序的。现假设它们落到不同的桶中，设分别为B[i']和B[j']。不失一般性，假设i' i'=floor(n*A[i])≥floor(n*A[j])=j' 得矛盾 (因为i' 来分析算法的运行时间。除第5行外，所有各行在最坏情况的时间都是O(n)。第5行中检查所有桶的时间是O(n)。分析中唯一有趣的部分就在于第5行中插人排序所花的时间。

为分析插人排序的时间代价，设ni为表示桶B[i]中元素个数的随机变量。因为插入排序以二次时间运行，故为排序桶B[i]中元素的期望时间为E[O(ni2)]=O(E[ni2])，对各个桶中的所有元素排序的总期望时间为：O(n)。(1) 为了求这个和式，要确定每个随机变量ni的分布。我们共有n个元素，n个桶。某个元素落到桶B[i]的概率为l/n，因为每个桶对应于区间[0，1)的l/n。这种情况与投球的例子很类似：有n个球 (元素)和n个盒子 (桶)，每次投球都是独立的，且以概率p=1/n落到任一桶中。这样，ni=k的概率就服从二项分布B(k;n,p)，其期望值为E[ni]=np=1，方差V[ni]=np(1-p)=1-1/n。对任意随机变量X，有右图所示表达式。

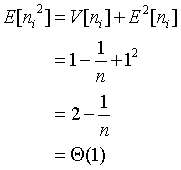
(2)将这个界用到(1)式上，得出桶排序中的插人排序的期望运行时间为O(n)。因而，整个桶排序的期望运行时间就是线性的。

代价

桶排序利用函数的映射关系，减少了几乎所有的比较工作。实际上，桶排序的f(k)值的计算，其作用就相当于快排中划分，已经把大量数据分割成了基本有序的数据块(桶)。然后只需要对桶中的少量数据做先进的比较排序即可。

对N个关键字进行桶排序的时间复杂度分为两个部分：

(1) 循环计算每个关键字的桶映射函数，这个时间复杂度是O(N)。

(2) 利用先进的比较排序算法对每个桶内的所有数据进行排序，其时间复杂度为 ∑ O(Ni*logNi) 。其中Ni 为第i个桶的数据量。

很显然，第(2)部分是桶排序性能好坏的决定因素。尽量减少桶内数据的数量是提高效率的唯一办法(因为基于比较排序的最好平均时间复杂度只能达到O(N*logN)了)。因此，我们需要尽量做到下面两点：

(1) 映射函数f(k)能够将N个数据平均的分配到M个桶中，这样每个桶就有[N/M]个数据量。

(2) 尽量的增大桶的数量。极限情况下每个桶只能得到一个数据，这样就完全避开了桶内数据的“比较”排序操作。当然，做到这一点很不容易，数据量巨大的情况下，f(k)函数会使得桶集合的数量巨大，空间浪费严重。这就是一个时间代价和空间代价的权衡问题了。

对于N个待排数据，M个桶，平均每个桶[N/M]个数据的桶排序平均时间复杂度为：

O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM)

当N=M时，即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。

总结：桶排序的平均时间复杂度为线性的O(N+C)，其中C=N*(logN-logM)。如果相对于同样的N，桶数量M越大，其效率越高，最好的时间复杂度达到O(N)。当然桶排序的空间复杂度为O(N+M)，如果输入数据非常庞大，而桶的数量也非常多，则空间代价无疑是昂贵的。此外，桶排序是稳定的。

源码

io.open();//打开控制台

/**-------------------------------------------------------* 桶排序**------------------------------------------------------*/

桶排序假设输入元素均匀而独立分布在区间[0,1) 即 0 <= x and x < 1;将区间划分成n个相同大小的子区间(桶)，然后将n个输入按大小分布到各个桶中去，对每个桶内部进行排序。最后将所有桶的排序结果合并起来.

//插入排序算法

insert_sort = function( array ){

for( right=2;#array ) {

var top = array[right];

//Insert array[right] into the sorted seqquence array[1....right-1]

var left = right -1;

while( left and array[left]>top){

array[left+1] = array[left];

left--;

}

array[left+1] = top;

}

return array;

}

//桶排序算法

bucket_sort = function( array ){

var n = #array;

var bucket ={}

for(i=0;n;1){

bucket[i] = {} //创建一个桶

}

var bucket_index

for(i=1;n;1){

bucket_index = math.floor(n * array[i]);

table.push( bucket [ bucket_index ],array[i] );//放到桶里去

}

for(i=1;n;1){

insert_sort( bucket[i] ); //对每个桶进行插入排序

}

return table.concat( table.unpack(bucket) )

}

io.print("----------------")

io.print("桶排序")

io.print("----------------")

array={};

//桶排序假设输入是由一个随机过程产生的小数.

math.randomize()

for(i=1;20;1){

table.push( array,math.random() )

}

//排序

array = bucket_sort( array )

//输出结果

for(i=1;#array;1){

io.print( array[i] )

}

execute("pause") //按任意键继续

io.close();//关闭控制台

C++

#include<iostream>

usingnamespace std;

int a[]={1,255,8,6,25,47,14,35,58,75,96,158,657};

const int len=sizeof(a)/sizeof(int);

int b[10][len+1]={0};//将b全部置0

void bucketSort(int a[]);//桶排序函数

void distribute Elments(int a[],int b[10][len+1],int digits);

void collectElments(int a[],int b[10][len+1]);

int numOfDigits(int a[]);

void zeroBucket(int b[10][len+1]);//将b数组中的全部元素置0

int main()

{

cout<<"原始数组：";

for(int i=0;i<len;i++)

cout<<a[i]<<",";

cout<<endl;

bucketSort(a);

cout<<"排序后数组：";

for(int i=0;i<len;i++)

cout<<a[i]<<",";

cout<<endl;

return 0;

}

void bucketSort(int a[])

{

int digits=numOfDigits(a);

for(int i=1;i<=digits;i++)

{

distributeElments(a,b,i);

collectElments(a,b);

if(i!=digits)

zeroBucket(b);

}

int numOfDigits(int a[])

{

int largest=0;

for(int i=0;i<len;i++)//获取最大值

if(a[i]>largest)

largest=a[i];

int digits=0;//digits为最大值的位数

while(largest)

{

digits++;

largest/=10;

}

return digits;

}

void distributeElments(int a[],int b[10][len+1],int digits)

{

int divisor=10;//除数

for(int i=1;i<digits;i++)

divisor*=10;

for(int j=0;j<len;j++)

{

int numOfDigist=(a[j]%divisor-a[j]%(divisor/10))/(divisor/10);

//numOfDigits为相应的(divisor/10)位的值,如当divisor=10时,求的是个位数

int num=++b[numOfDigist][0];//用b中第一列的元素来储存每行中元素的个数

b[numOfDigist][num]=a[j];

}

void collectElments(int a[],int b[10][len+1])

{

int k=0;

for(int i=0;i<10;i++)

for(int j=1;j<=b[i][0];j++)

a[k++]=b[i][j];

}

void zeroBucket(int b[][len+1])

{

for(int i=0;i<10;i++)

for(int j=0;j<len+1;j++)

b[i][j]=0;

}

JAVA

public static void basket(int data[])//data为待排序数组

{

int n=data.length;

int bask[][]=new int[10][n];

int index[]=new int[10];

int max=Integer.MIN_VALUE;

for(int i=0;i<n;i++)

{

max=max>(Integer.toString(data[i]).length())?max:(Integer.toString(data[i]).length());

}

String str;

for(int i=max-1;i>=0;i--)

{

for(int j=0;j<n;j++)

{

str="";

if(Integer.toString(data[j]).length()<max)

{

for(int k=0;k<max-Integer.toString(data[j]).length();k++)

str+="0";

}

str+=Integer.toString(data[j]);

bask[str.charAt(i)-'0'][index[str.charAt(i)-'0']++]=data[j];

}

int pos=0;

for(int j=0;j<10;j++)

{

for(int k=0;k<index[j];k++)

{

data[pos++]=bask[j][k];

}

for(intx=0;x<10;x++)index[x]=0;

}

PAS

program barrel_sort;

var

a:array[0..100] of integer;

i,k,n:integer;

begin

for i:=0 to 100 do a[i]:=0;{初始化}

readln(n);

for i:=1 to n do

begin

read(k);

a[k]:=a[k]+1;{将等于k的值全部装入第k桶中}

end;

for i:=0 to 100 do

while a[i]>0 do

begin

write(i:6);

a[i]:=a[i]-1;

end;{输出排序结构}

end.

//这段应该是鸽巢排序，桶排序应该有段桶内比较排序的函数

应用

海量数据

一年的全国高考考生人数为500 万，分数使用标准分，最低100 ，最高900 ，没有小数，要求对这500 万元素的数组进行排序。

分析：对500W数据排序，如果基于比较的先进排序，平均比较次数为O(5000000*log5000000)≈1.112亿。但是我们发现，这些数据都有特殊的条件： 100=<score<=900。那么我们就可以考虑桶排序这样一个“投机取巧”的办法、让其在毫秒级别就完成500万排序。

方法：创建801(900-100)个桶。将每个考生的分数丢进f(score)=score-100的桶中。这个过程从头到尾遍历一遍数据只需要500W次。然后根据桶号大小依次将桶中数值输出，即可以得到一个有序的序列。而且可以很容易的得到100分有***人，501分有***人。

实际上，桶排序对数据的条件有特殊要求，如果上面的分数不是从100-900，而是从0-2亿，那么分配2亿个桶显然是不可能的。所以桶排序有其局限性，适合元素值集合并不大的情况。

典型

在一个文件中有10G个整数，乱序排列，要求找出中位数。内存限制为2G。只写出思路即可（内存限制为2G意思是可以使用2G空间来运行程序，而不考虑本机上其他软件内存占用情况。）关于中位数：数据排序后，位置在最中间的数值。即将数据分成两部分，一部分大于该数值，一部分小于该数值。中位数的位置：当样本数为奇数时，中位数=(N+1)/2 ; 当样本数为偶数时，中位数为N/2与1+N/2的均值（那么10G个数的中位数，就第5G大的数与第5G+1大的数的均值了）。

分析：既然要找中位数，很简单就是排序的想法。那么基于字节的桶排序是一个可行的方法。

思想：将整型的每1byte作为一个关键字，也就是说一个整形可以拆成4个keys，而且最高位的keys越大，整数越大。如果高位keys相同，则比较次高位的keys。整个比较过程类似于字符串的字典序。

第一步:把10G整数每2G读入一次内存，然后一次遍历这536,870,912即（1024*1024*1024）*2 /4个数据。每个数据用位运算">>"取出最高8位(31-24)。这8bits(0-255)最多表示256个桶，那么可以根据8bit的值来确定丢入第几个桶。最后把每个桶写入一个磁盘文件中，同时在内存中统计每个桶内数据的数量NUM[256]。

代价：(1) 10G数据依次读入内存的IO代价(这个是无法避免的，CPU不能直接在磁盘上运算)。(2)在内存中遍历536,870,912个数据，这是一个O(n)的线性时间复杂度。(3)把256个桶写回到256个磁盘文件空间中，这个代价是额外的，也就是多付出一倍的10G数据转移的时间。

第二步：根据内存中256个桶内的数量NUM[256]，计算中位数在第几个桶中。很显然，2,684,354,560个数中位数是第1,342,177,280个。假设前127个桶的数据量相加，发现少于1,342,177,280，把第128个桶数据量加上，大于1,342,177,280。说明，中位数必在磁盘的第128个桶中。而且在这个桶的第1,342,177,280-N(0-127)个数位上。N(0-127)表示前127个桶的数据量之和。然后把第128个文件中的整数读入内存。(若数据大致是均匀分布的，每个文件的大小估计在10G/256=40M左右，当然也不一定，但是超过2G的可能性很小)。注意，变态的情况下，这个需要读入的第128号文件仍然大于2G，那么整个读入仍然可以按照第一步分批来进行读取。

代价：(1)循环计算255个桶中的数据量累加，需要O(M)的代价，其中m<255。(2)读入一个大概80M左右文件大小的IO代价。

第三步：继续以内存中的某个桶内整数的次高8bit（他们的最高8bit是一样的）进行桶排序(23-16)。过程和第一步相同，也是256个桶。

第四步：一直下去，直到最低字节(7-0bit)的桶排序结束。我相信这个时候完全可以在内存中使用一次快排就可以了。

整个过程的时间复杂度在O(n)的线性级别上(没有任何循环嵌套)。但主要时间消耗在第一步的第二次内存-磁盘数据交换上，即10G数据分255个文件写回磁盘上。一般而言，如果第二步过后，内存可以容纳下存在中位数的某一个文件的话，直接快排就可以了（修改者注：我想，继续桶排序但不写回磁盘，效率会更高？）。