第18章条件概率

18.1蒙特霍尔困惑

对于上一章的三个门的问题，有一个漏洞。假设参赛者选择门A且门B后有一只山羊，刚好产生3个结果：

以上结果出现的概率分别是1/18,1/18,1/9。

在这些结果中，只有最后一个结果(C,A,B)，换门才能获胜。另外两个结果的概率加起来等于1/9，这与最后一个结果的概率相同。因此这时，转换选择获胜的概率与失败的概率是相等的。

以上结论其实是不对的，因为换门胜利的概率是1/2这个结论是在是在给定另一个事件发生的条件下求得。

表示这个概率,根据刚才的推理它等于1/2。

18.1.1帷幕之后

“给定”条件的本质是指引我们只关注某一部分结果。正式的说法是，定义一个只包含某部分结果的样本空间。该例子的样本空间为以上的三个结果。

这一计算过程并没有错误，为什么由它得出的换不换门的结论是错误的呢?因为它计算的对象错了。

18.2定义和标记

表达式Pr[X|Y]表示，在事件Y发生的条件下，事件X发生的概率。

定义18.2.1：设X和Y是事件，且Y具有非零概率，那么，

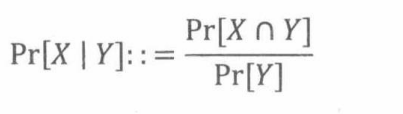
18.2.1问题所在

那么，如果18.1节的推理在数学上是合理的，为什么它看起来又与第17章得到的结论相矛盾呢?这是一个常见的问题:我们选择了错误的条件。正确的条件概率应当是“给定参赛者选择门A且卡洛打开门B的条件下，换门获胜的概率是多少”。这时样本空间就不会包含（A，A，C）。

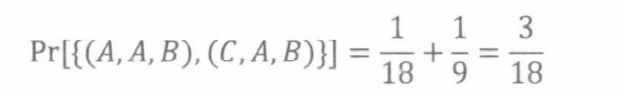
于是条件概率为:

18.3条件概率四步法

一场三局两胜的比赛，第一场获胜的概率是1/2，如果前一场胜了，那么下一层获胜的概率是2/3，如果上一场输了，那么下一场获胜的概率的1/3。问题是在第一场获胜的前提下，取得最终胜利的概率为多少。

树状图如下所示：

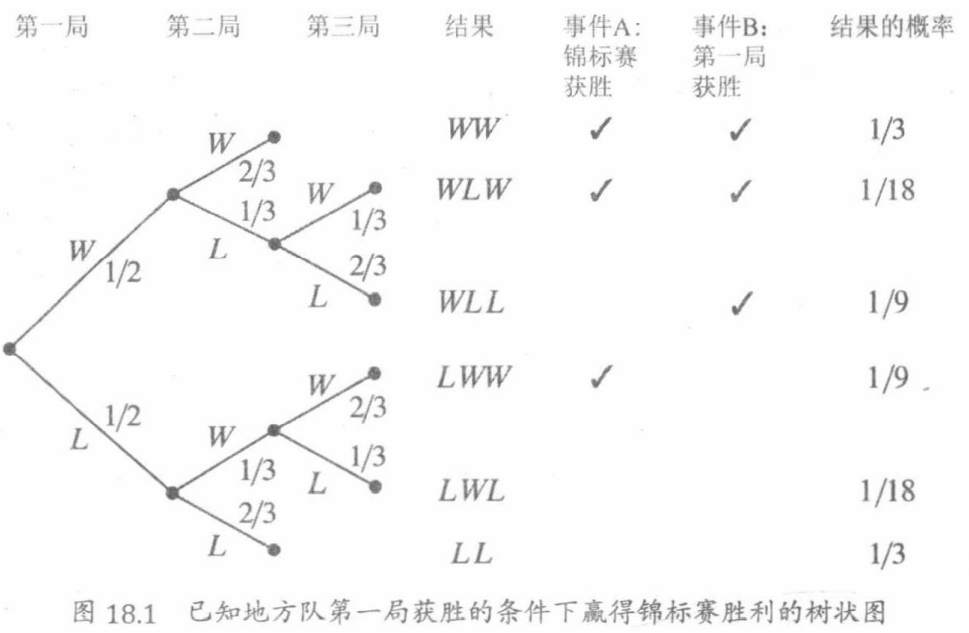
步骤一:确定样本空间

完整的样本空间是:

步骤二:定义目标事件

地方队赢得锦标赛的事件:

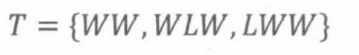
以及地方队赢得第一局的事件:

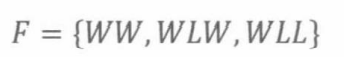
步骤三:确定结果的概率

接下来，我们必须为每个结果分配概率。首先,根据问题定义，给每条边赋值。然后，我们把根到叶子路径上的所有边的概率相乘，得到对应的结果的概率。例如，事件WLL的概率是:

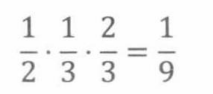
步骤四:计算事件的概率

现在我们可以计算，在已知赢得第一局的条件下，地方队赢得锦标赛的概率

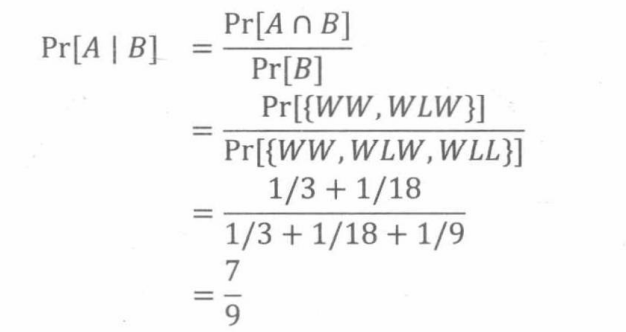
18.4为什么树状图有效

为什么这些图是有效的?

这涉及条件概率。事实上，树状图中边的概率就是条件概率。一般来说，树状图上的每一条边的概率是指，给定从根节点到父节点的条件下实验沿着这条路径推进到当前节点的概率。

法则(条件概率的乘法法则:两个事件)

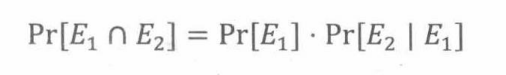
树状图的边概率相乘等于这个等式的右侧。例如:

法则(条件概率的乘法法则:三个事件)

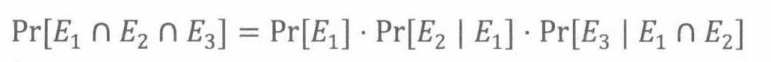
18.4.1 大小为k的子集的概率

条件概率乘法法则的一个简单应用就是，计算整数[1…n]内大小为k的子集的数量。

选择某个大小为k的子集S ⊂ [1…n]作为目标。设p是随机选择这个目标子集的概率。也就是说,选择S的概率是p,而所有子集被选中的概率相等，所以大小为k的子集数量等于1/p 。

那么p是多少呢?首先，随机目标集合S中最小的数即k个数中最小的一个，其概率是k /n。然后，在给定S中最小数的条件下，第二小的数在剩下k-1个数中的概率是(k -1)/(n- 1)。那么,根据乘法法则,两个最小的数同时在S中的概率为

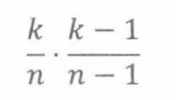
用这种方法继续计算，很容易得出随机选择的所有k个数全部在S中，即随机选择的集合就是目标集合S的概率是

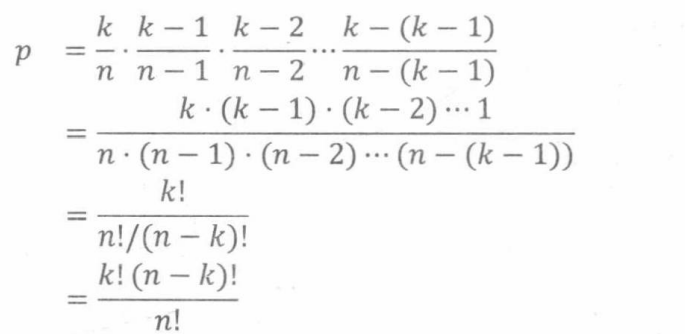
于是，我们再一次得出了[1…n]上大小为k的子集的数量，即1/p，等于

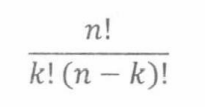
18.4.2医学检测

当前的乳腺X光检测大概有90%到95%的正确率，作为一种并不昂贵的无创检查，这样的准确率似乎已经很不错了。然而，乳腺X光检测结果也例证了条件概率与直觉相悖。

首先我们给出乳腺X光检测的精确定义:

18.4.3四步分析法

现在假设我们检测的对象是没有家族癌症病史的中年妇女，这一人群的乳腺癌发病率不超过1%。
步骤一:确定样本空间

步骤二:确定目标事件

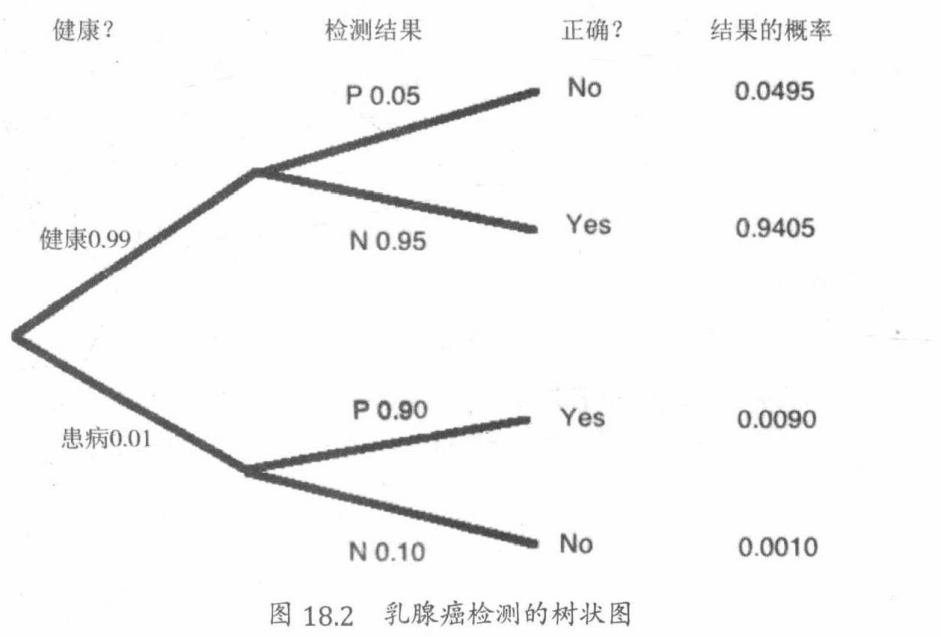
设事件A为被检测者实际患有乳腺癌，事件B为检测结果为阳性。每个事件中的结果被标在树状图上。我们想确定Pr[A |B],即给定检测结果为阳性的条件下被检测者患有乳腺癌的概率。

步骤三:计算结果的概率
首先确定边的概率。根据问题定义和乘法法则，每个结果的概率等于根到叶子的路径上所有边的概率之积。如图18.2所示。

步骤四:计算事件的概率

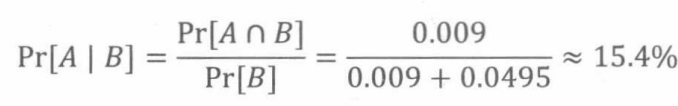
因此，如果检测结果为阳性，有84.6%的可能性这个检测结果是错误的!

18.4.4固有频率

实际患病的人的检测结果为阳性的概率只有15%，初看起开这似乎很令人吃惊。

考虑用“固有频率”来理解这些令人费解的结果例如，让我们来仔细考察乳腺X光检测的例子。

考察10000名女性。根据患病率，她们中的100个人可能患有乳腺癌其中又有90个会有阳性检测结果。剩下9900个人为健康女性，但是她们中有5%—约500人—会在乳腺X光检测中得到假阳性结果。这就是说，每不到600个阳性结果中只有90个是真正的阳性。所以，错误率为85%。

18.4.5后验概率

如果事件B在时间上先于事件A发生，那么条件概率Pr[B|A]称为后验概率。

假设我们将冰球队问题反过来:给定本地冰球队赢了锦标赛的条件下，他们赢得了第一局的概率是多少?

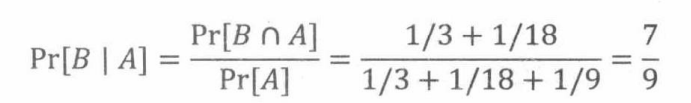
一般地，贝叶斯法则描述了这两种概率的关系。

定理18.4.1(贝叶斯公式)

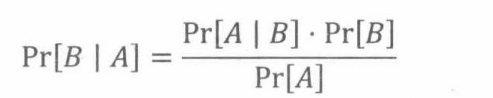
18.5 全概率定理

将概率计算拆分成不同的情况，能够简化很多问题。

法则18.5.1（全概率定理:单一事件)

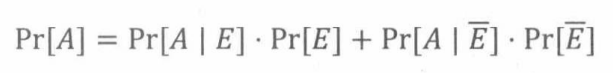
法则（全概率公式:三个事件）若 $E_1,E_2,和E_3$ 是不相交的，且 $Pr[E_1 \cup E_2\cup E_3]=1$ ，那么

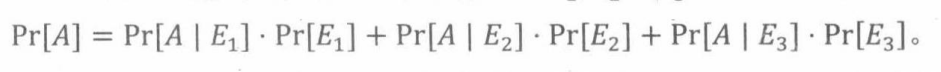
由此可得三个事件的贝叶斯公式，即根据给定 $E_1,E_2,和E_3$ 时A的条件概率“反过来”求给定A时 $E_1$ 的条件概率:

法则(贝叶斯法则:三个事件)：

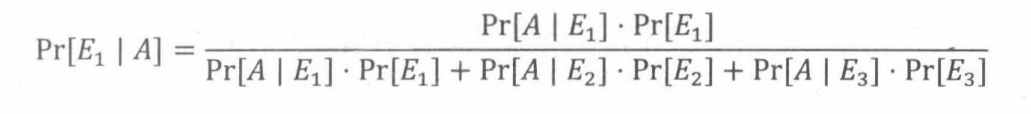
18.5.1以单一事件为条件

两个集合的容斥公式当所有概率都以事件C为条件时仍然成立:

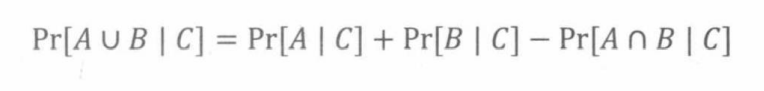
但是，下面这个式子是错的：

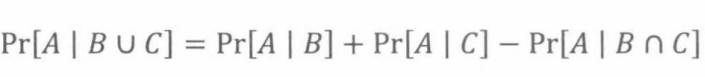
18.6辛普森悖论

辛普森悖论：即多个数据组呈现出类似的趋势，而这些数据组聚合起来呈现相反的趋势。要解释为什么会发生这种情况，首先我们使用条件概率理清问题。

某学校有两个系:EE和CS。进行随机选择一个候选人的试验。定义如下事件:

录情情况如表18-1所示。

男性候选人比女性候选人更容易被录取-—-可以表述为如下不等式:

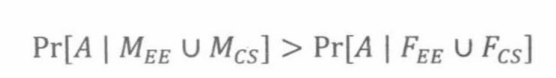
对任何系来说，女性申请者都比男性申请者更容易被录取——可以表述为:

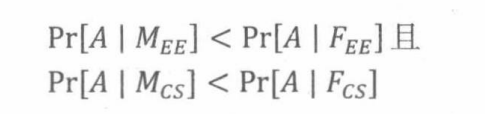
我们可以这么解释为什么全校整体录取率与系的录取情况存在差异:CS系比EE系更加苛刻,而CS系的女性申请者远远多于EE系。

事实上，我们对数据相关性的解释,取决于我们对影响录取的因素的最初信念。”这个例子强调了一个常常被忽视的统计学基本原理：永远不要假设相关关系意味着因果关系。

18.7 独立性

定义18.7.1：概率为0的事件是指独立于所有事件(包括它自己)的事件
如果 Pr[B]≠0, 那么事件A独立于事件B当且仅当

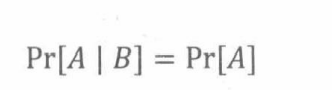
潜在陷阱

学生们有时觉得不相交的事件是独立的。这句话的否命题是成立的:如果A∩B 等于空集，那么如果A发生B就不会发生。不相交的事件不可能是独立的—除非其中一个事件的概率为0。

18.7.1另一个公式

定理18.7.2 A独立于B，当且仅当

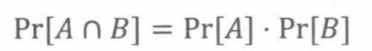
推论18.7.3 A独立于B当且仅当B独立于A。

18.7.2 独立性是一种假设

一般来说，独立性是建模时做出的假设。

判断何时该假设两个事件是独立的是一件棘手的事情。在实践中,由于很多有用的公式只在事件独立时成立，所以我们总是很想去假设独立性。但是你必须小心:我们将介绍几个著名的错误假设独立性带来麻烦的例子。如果不止两个事件，问题会变得更加棘手。

18.8相互独立性

如何定义两个以上的事件的独立性

给定一个事件集合，对其中任意一个事件来说，不论其他事件是否发生都不影响这个事件发生的概率，那么我们说这个事件集合是相互独立的。
另一种等价的说法是:对任意选择的两个及以上事件来说，这些事件同时发生的概率等于每一个事件发生概率的乘积。

18.8.1 DNA检测

在实践中，独立性假设稀松平常，而且大多是非常合理的。然而有时候独立性假设的合理性并不明显，而错误假设的后果是很严重的。

血液遗传标记与随机样本吻合的可能性至多为1亿7000万分之一。这个天文数字是从这样的统计数据中得出的:

将这些数字相乘，可得一个随机选择的人同时具有5个标记的概率:

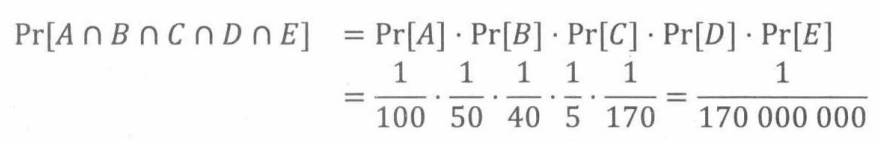
18.8.2两两独立

定义18.8.1：一个事件集合A1,A2,…是k-次独立的，当且仅当其中k个事件构成的子集是相互独立的。这个事件集合是两两独立的，当且仅当它是2-次独立的。

例如：如果上文中的A，B，C，D，E是两两独立的，则：

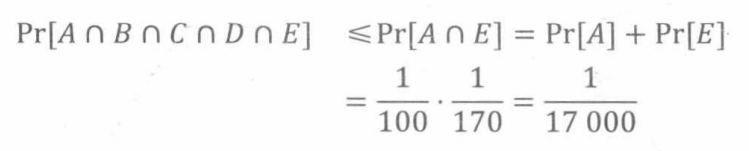
所以,更强的独立性假设能够为匹配概率提供更小的上界。重点是确定合理的独立性假设。

18.9 概率vs.置信度

18.9.1肺结核测试

令事件“TB”为一个人患有肺结核，事件“pos”为一个人肺结核测试为阳性。令：

这意味着，无论一个人是否真的有肺结核，这一测试99%产生的都是正确结果。一个谨慎的统计学家会做出以下断言:

引理18.9.1：你能够99%地确信测试结果是正确的。
推论18.9.1：如果检测结果是阳性，那么要么患有肺结核，要么发生了某件很不可能的事情(概率为1/100 )。

引理18.9.1和推论18.9.1看起来说的是：如果检测结果是阳性的，那么患有肺结核的概率是0.99。（错的）

实际上，上面那句话是错的

当检测结果为阳性时，我们似乎认为患有肺结核的可能性更大。但是,实际得肺结核的概率比测试出错的概率还要小很多。所以，我们应该认为是诊断出错了，而不是的肺结核。

18.9.2可能性修正

贝叶斯更新
将测试的概率转换成结果的概率，一个标准的方法就是使用贝叶斯定理（参见式18.2)。用“可能性”( odds)代替概率,重新阐述贝叶斯定理。

若H为一个事件，定义H的可能性为

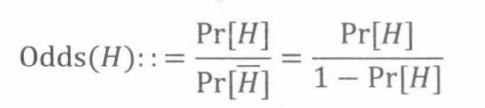
其中

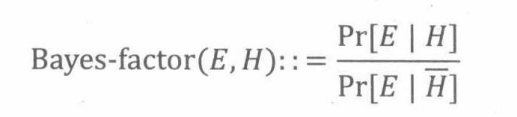
引理18.9.2

肺结核测试的可能性

所以阳性测试结果将患肺结核的可能性提高了100倍，也就是说，阳性测试结果是支持肺结核诊断的显著证据。

如果：

则

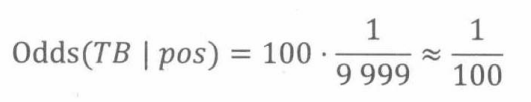
则，如果一个人被测试为阳性，那么他得肺结核的概率为1/100。

18.9.3很可能正确的事实

我们已经知道，如果一个随机的人被肺结核测试检测为阳性，那么他患病的概率大概是1/100。如果就是你不巧被检测为肺结核阳性，一个称职的医生一般会告诉你，你得肺结核的概率从1/10 000提高到1/100。但真的是这样吗?不见得。

医生做出判断的依据是，他认为与得肺结核相关的个体因素，或者考虑到误诊后果的严重性等。这些是很重要的医学判断，但不是数学判断。不同医生对于“像你一样的人”有着不同的判断，因此也会给出不同的概率。不存在关于你是谁的“正确”模型也不存在精确到个体的患肺结核的正确概率。

18.9.4 极端事件

公平硬币是指抛得正面和抛得反面概率都是1/2的硬币。设想抛一枚硬币100次,而且每次都得到正面。你觉得下一次还会抛得正面的可能性是多少?

根据“公平硬币”的定义，下一次抛得正面的概率依然是1/2。

一枚公平硬币抛得100次正面的概率小到可以忽略不计，这就动摇了这是一枚公平硬币的假设。那么，我们假设有两枚硬币:一枚是公平的，一枚是有偏向的，且有99/100的概率抛得正面。随机选择其中一枚硬币，但是公平硬币被选到的概率要大得多，有偏向的硬币被选到的概率只有 $2^{-50}$ 。将这个选中的硬币抛掷100次。令事件E为抛得100次正面，事件H为选择的是有偏向的硬币。

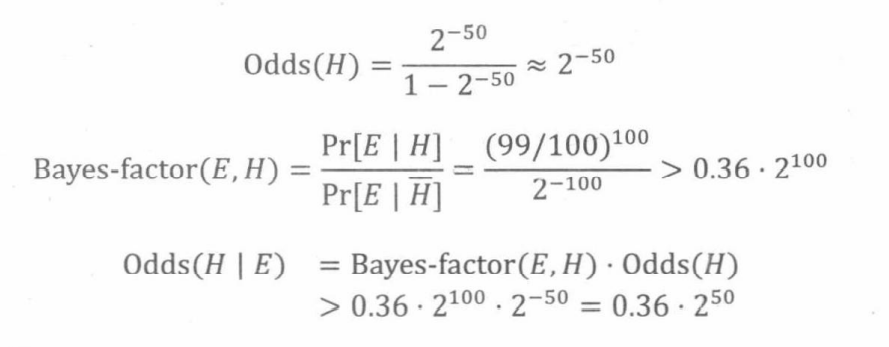
这表明，抛得100次正面之后，有偏向的硬币被选中的可能性压倒性地大，所以下一次也有很大概率抛得正面。

18.9.5下一次抛掷的置信度

如果考虑的是置信度而不是概率，就不需要对公平硬币的概率做任何贝叶斯假设。我们知道，如果抛得100次正面，则要么硬币是有偏向的，要么某个几乎不可能发生的事（概率为 $2^{-100}$ ）发生了。这意味着我们可以断言硬币有偏向的置信水平是1- $2^{-100}$ 。简单来说，如果掷得100次正面，我们差不多可以100%地确信这枚硬币是有偏向的。
件E为抛得100次正面，事件H为选择的是有偏向的硬币。