Matlab（数值微积分）

news2024/10/7 14:30:08

目录

1.多项式微分与积分

1.1 微分

1.2 多项式微分

1.3 如何正确的使用Matlab?

1.3.1 Matlab表达多项式

1.3.2  polyval() 多项式求值

 1.3.3 polyder()多项式微分

1.4 多项式积分

1.4.1 如何正确表达

1.4.2 polyint() 多项式积分

2.数值的微分与积分

2.1 数值微分

 2.2 diff() 计算差值

  2.3 误差的准确性

 2.4 二阶、三阶导数

 2.5 数值积分

 2.5.1中点规则

 2.5.2 梯形规则（trapz）

2.5.3 辛普森积分法

2.5.4 三种积分方式比较

3.函数句柄

3.1 创建函数句柄

 3.1.1 有参数的句柄函数

3.1.2 无参数的句柄函数

3.1.3 无参且无括号

3.2 匿名函数

3.3 错误示范

3.4 integral() 数值积分

3.4.1 一级积分

3.4.2 integral2() 二级积分

3.4.3 integral3() 三级积分

1.多项式微分与积分

1.1 微分

  • 函数f(x)导数写为：F'(x)或者 \frac{df(x)}{dx}
  • 函数f(x)关于x的变化率

f (x0) 表示点x0处曲线相切的直线的系数。

1.2 多项式微分

对于一个多项式：f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}   来说，其微分多项式为：

f(x)=a_{n}nx^{n-1}+a_{n-1}(n-1)x^{n-2}+...+2a_{2}x+a_{1}

1.3 如何正确的使用Matlab?

1.3.1 Matlab表达多项式

f(x)=x^{3}-2x-5  

在上式中，我们用Matlab应该怎么进行表示（多项式在Matlab中被表示为行向量）

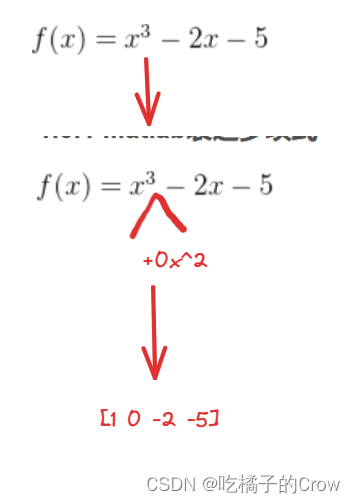
>> p=[1 0 -2 -5]

p =

     1     0    -2    -5

1.3.2  polyval() 多项式求值

语法：y=polyval(p,x)

y= polyval(p,x) 计算多项式 p 在 x 的每个点处的值。参数 p 是长度为 n+1 的向量，其元素是 n 次多项式的系数（降幂排序）：

p(x)=p_{1}x^{n}+p_{2}x^{n-1}+...+p_{n-1}x+p_{n}+1

示例1：

计算多项式 p(x)=3x^2+2x+1在点 x=5、7 、9 处的值。

>> p = [3 2 1];
x = [5 7 9];
y = polyval(p,x)

y =

    86   162   262

 示例2：

f(x)=9x^{3}-5x^{2}+3x+7   (-2<=x<=5) 

对该多项式进行画图求值

>> a = [9,-5,3,7]; x = -2:0.01:5;
f = polyval(a,x);
plot(x,f,'LineWidth', 2);%设置线条粗度
xlabel('x轴'); ylabel('f(x)');%设置xy轴名称
set(gca, 'FontSize', 14)%设置字体大小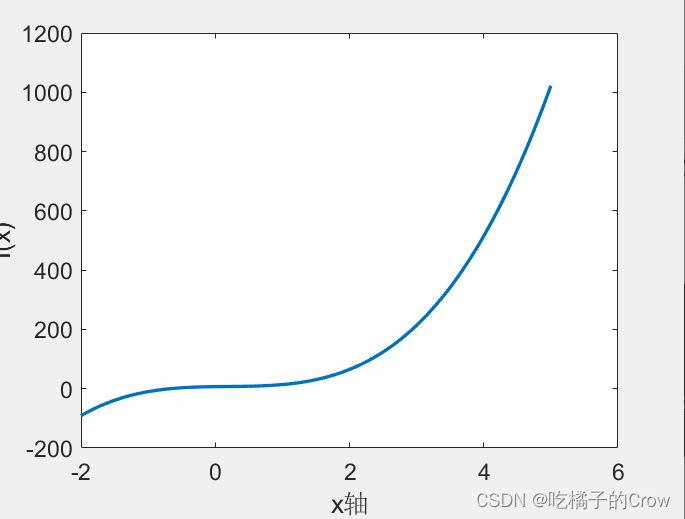

 1.3.3 polyder()多项式微分

语法一：k=polyder(p)

k=polyder(p)返回的p中的系数表示的多项式的导数  k(x)=\frac{d}{dx}p(x)

示例：

创建一个向量来表示多项式 p(x)=3x^5−2x^3+x+5。

p = [3 0 -2 0 1 5];

 使用polyder对多项式进行求导，结果为： q(x)=15x^{4}-6x^{2}+1

q = polyder(p)
q = 1×5

    15     0    -6     0     1

 语法二：k= polyder(a,b) 返回多项式 a 和 b 的乘积的导数  k(x)=\frac{d}{dx}[a(x)b(x)]

示例：

创建两个向量来表示多项式 a(x)=x^4−2x^3+11 和 b(x)=x^2−10x+15。

a = [1 -2 0 0 11];
b = [1 -10 15];
q = polyder(a,b)
q = 1×6

     6   -60   140   -90    22  -110
最后的结果为:

语法三：[q,d] = polyder(a,b) 返回多项式 a 和 b 的商的导数 \frac{q(x)}{d(x)}=\frac{d}{dx}[\frac{a(x)}{b(x)}]

示例：

创建两个向量来表示商中的多项式    \frac{x^{4}-3x^{2}-1}{x+4}

p = [1 0 -3 0 -1];
v = [1 4];
[q,d] = polyder(p,v)
q = 1×5

     3    16    -3   -24     1

d = 1×3

     1     8    16

 结果为：

\frac{q(x)}{d(x)}=\frac{3x^{4}+16x^{3}-3x^{2}-24x+1}{x^{2}+8x+16}

1.4 多项式积分

对于一个多项式：f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}

 积分多项式为： \int f(x)=\frac{1}{n+1}a_{n}x^{n+1}+\frac{1}{n}a_{n-1}x^{n}+...+a_{0}x+k

1.4.1 如何正确表达

1.4.2 polyint() 多项式积分

语法：q=polyint(p,k) 如果只有的一个参数p，默认k是0，使用积分常量k返回p中的系数所表示的多项积分

示例：

对两个多项式的乘积求积分  I=\int_{0}^{2}(x^{5}-x^{3}+1)(x^{2}+1)dx

  • 创建向量来表示多项式
p = [1 0 -1 0 0 1];
v = [1 0 1];
  •  多项式相乘，并使用积分常量k=3对所生成的表达式求积分
k = 3;
q = polyint(conv(p,v),k)
q = 1×9

    0.1250         0         0         0   -0.2500    0.3333         0    1.0000    3.0000
  •  通过在积分范围上计算q来求解I的值
a = 0;
b = 2;
I = diff(polyval(q,[a b]))
I = 
     32.6667

2.数值的微分与积分

2.1 数值微分

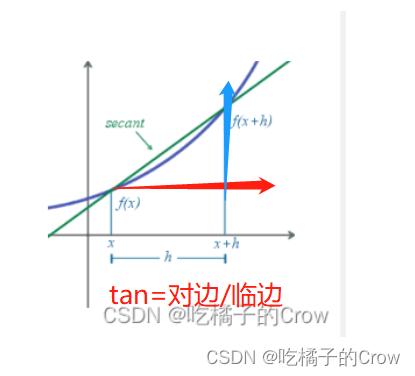
  • 最简单的方法：有限差分近似法
  • 计算x附近的割线   f'(x_{0})=\lim_{h \to0 } \frac{f((x_{0}+h)-f(x_{0}))}{h}  

​

 2.2 diff() 计算差值

diff() 计算向量中相邻元素之间的差值

x = [1 2 5 2 1];
diff(x)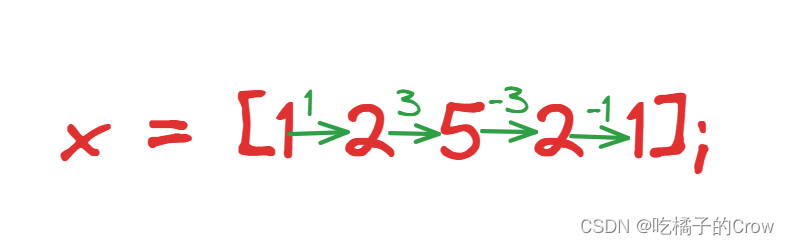

​

>> x = [1 2 5 2 1];
diff(x)

ans =

     1     3    -3    -1

 示例：

求出两点之间的斜率

​

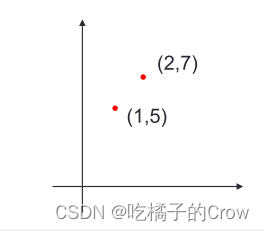
>> x = [1 2]; y = [5 7];
slope = diff(y)./diff(x) %y的变化量/x的变化量

slope =

     2

  2.3 误差的准确性

 f'(x_{0})=\lim_{h \to0 } \frac{f((x_{0}+h)-f(x_{0}))}{h}  当f(x)=sin(x)   h=0.1、0.01、0.001s时误差有什么变化？

当h=0.1时：

>> x0 = pi/2; h = 0.1;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)

m =

   -0.0500

当h=0.01时：

>> x0 = pi/2; h = 0.01;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)

m =

   -0.0050

当h=0.001时：

>> 
x0 = pi/2; h = 0.001;
x = [x0 x0+h];
y = [sin(x0) sin(x0+h)];
m = diff(y)./diff(x)

m =

  -5.0000e-04

由分析得：所以当h->0时，误差越小

g = colormap(lines); hold on;
for i=1:4
x = 0:power(10, -i):pi;
y = sin(x); m = diff(y)./diff(x);
plot(x(1:end-1), m, 'Color', g(i,:));%每次微分，系数的个数少1
end
hold off;
set(gca, 'XLim', [0, pi/2]); set(gca, 'YLim', [0, 1.2]);
set(gca, 'FontSize', 18); set(gca, 'FontName', 'symbol');
set(gca, 'XTick', 0:pi/4:pi/2);
set(gca, 'XTickLabel', {'0', 'p/4', 'p/2'});
h = legend('h=0.1','h=0.01','h=0.001','h=0.0001');
set(h,'FontName', 'Times New Roman'); box on;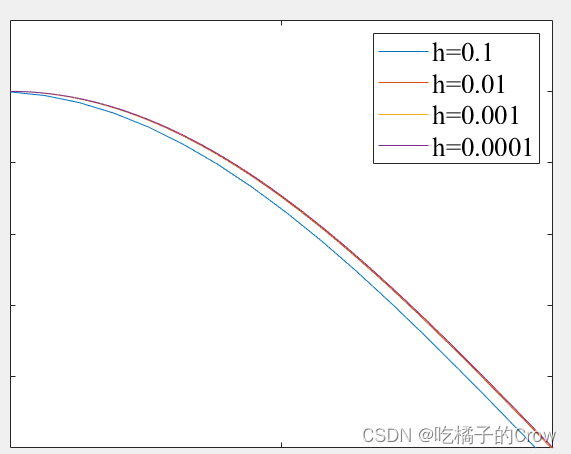

​

 2.4 二阶、三阶导数

f(x)=x^{3}     (-2<=x<=2)

>> x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x);
m2 = diff(m)./diff(x(1:end-1));
plot(x,y,x(1:end-1),m,x(1:end-2),m2);%每次导数系数减1
xlabel('x', 'FontSize', 18);
ylabel('y', 'FontSize', 18);
legend('f(x) =x^3','f''(x)','f''''(x)');
set(gca, 'FontSize', 18);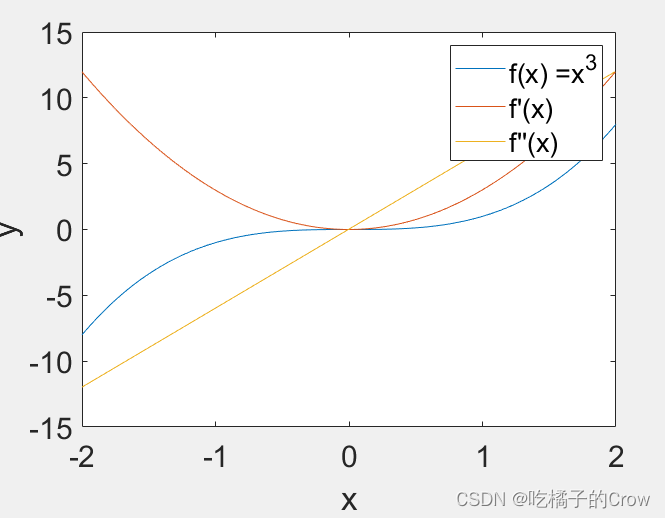

​

 2.5 数值积分

s=\int_{a}^{b}f(x)d(x)\approx \sum_{i=0}^{n}f(x_{i})\int_{a}^{b}L_{i}(x)dx

  • 求积法——用有限集点逼近积分

​

​

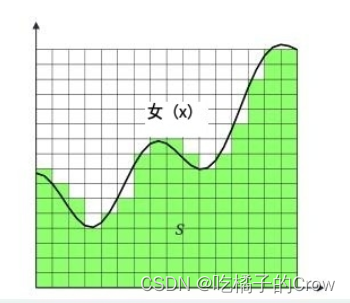
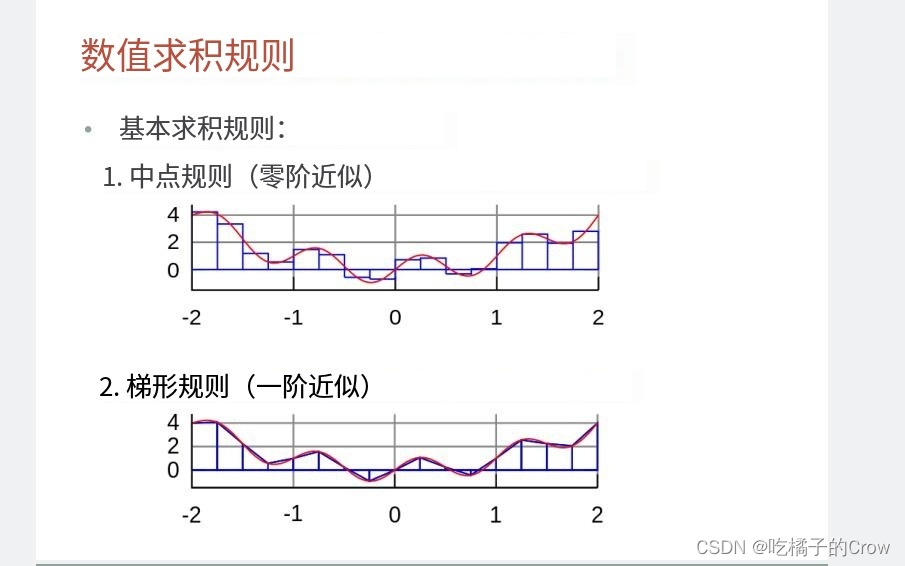
 2.5.1中点规则

​

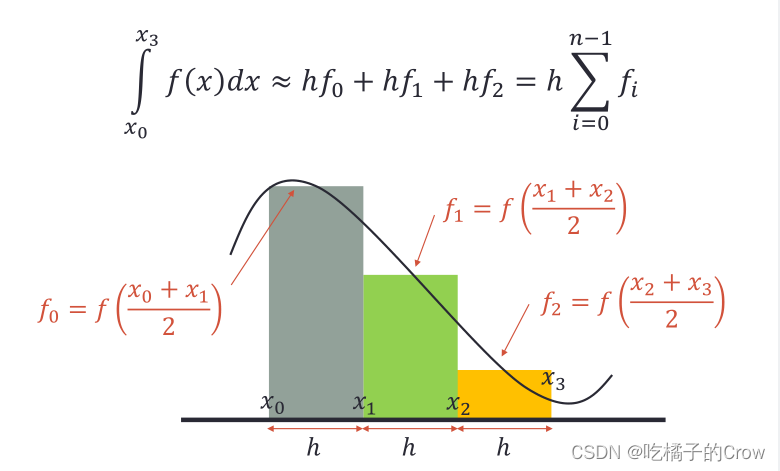
 示例：

我们通过积分可以求得：

A=\int_{0}^{2}4x^{3}dx=x^{4}|_{0}^{2}=(2)^{4}-(0)^{4}=16

但是我们通过中点积分可得：

>> h = 0.05; x = 0:h:2;
midpoint = (x(1:end-1)+x(2:end))./2;
y = 4*midpoint.^3;
s = sum(h*y)

s =

   15.9950

解释：

midpoint = (x(1:end-1)+x(2:end))./2;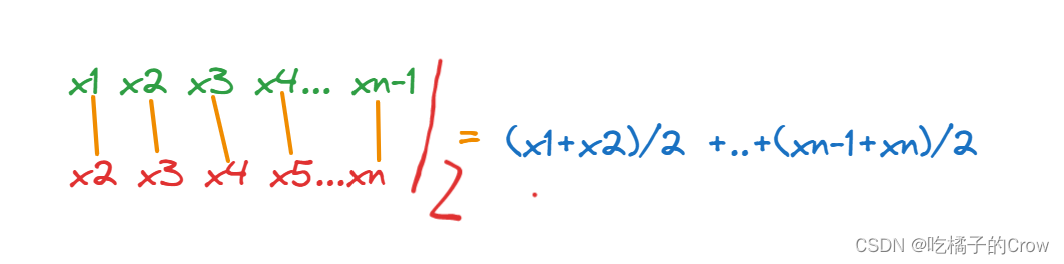

​

 2.5.2 梯形规则（trapz）

​

 A=\int_{0}^{2}4x^{3}dx=x^{4}|_{0}^{2}=(2)^{4}-(0)^{4}=16

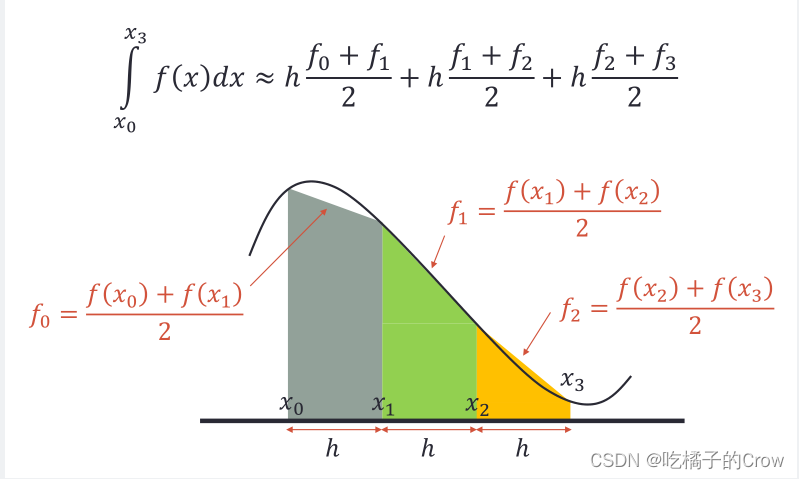
>> h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h*trapz(y)

s =

   16.0100

我们也可以自定义该函数：

h = 0.05; x = 0:h:2; y = 4*x.^3;
trapezoid = (y(1:end-1)+y(2:end))/2;
s = h*sum(trapezoid)

s =

   16.0100

2.5.3 辛普森积分法

​

 A=\int_{0}^{2}4x^{3}dx=x^{4}|_{0}^{2}=(2)^{4}-(0)^{4}=16


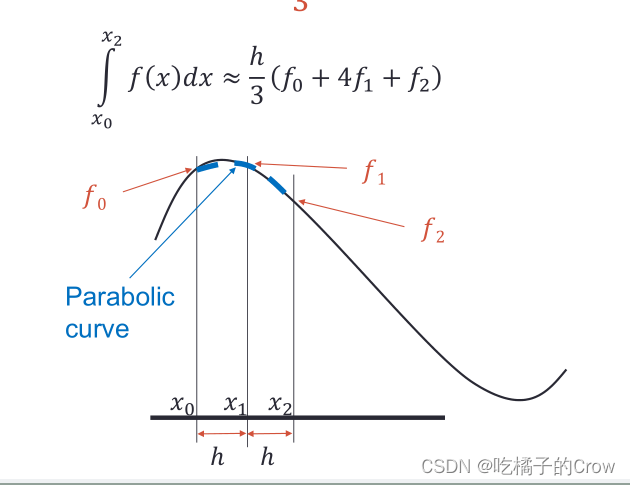
>> h = 0.05; x = 0:h:2; y = 4*x.^3;
s = h/3*(y(1)+2*sum(y(3:2:end-2))+...
4*sum(y(2:2:end))+y(end))

s =

    16

2.5.4 三种积分方式比较

​

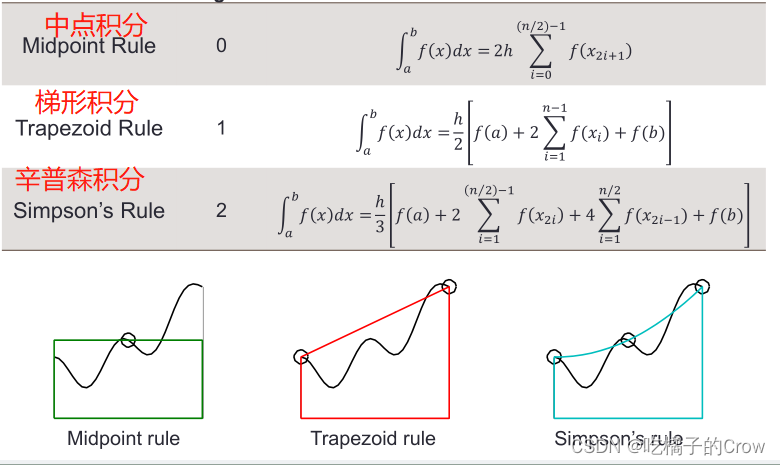
由分析易得： 辛普森积分法误差最小

3.函数句柄

       函数句柄是一种存储指向函数的关联关系的Matlab数据类型，间接调用函数使您在调用函数时无需考虑调用位置，函数句柄的典型用法包括：

  • 将一个函数传递到另一个函数（通常称为复合函数）
  • 指定回调函数
  • 构造以内联方式定义而非存储在程序文件(匿名函数)中的函数句柄
  • 从主函数外调用局部函数

查看h是否是函数句柄

isa(h,'function_handle')

3.1 创建函数句柄

通过在函数名称前添加一个 @ 符号来为函数创建句柄。

f = @myfunction;

 3.1.1 有参数的句柄函数

使用句柄调用函数的方式与直接调用函数一样，例如：

function y = computeSquare(x)
y = x.^2;
end

创建句柄并调用该函数以计算 4 的平方。

f = @computeSquare;
a = 4;
b = f(a)
b =

    16

3.1.2 无参数的句柄函数

如果该函数不需要任何输入，则您可以使用空括号调用该函数，例如：

h = @ones;
a = h()
a =

    1

3.1.3 无参且无括号

如果不使用括号，则该赋值会创建另一个函数句柄。

a = h
a = 

    @ones

3.2 匿名函数

        您可以创建指向匿名函数的句柄。匿名函数是基于单行表达式的 MATLAB 函数，不需要程序文件。构造指向匿名函数的句柄，方法是定义 anonymous_function 函数主体，以及指向匿名函数 arglist 的以逗号分隔的输入参数列表。语法为：

h = @(arglist)anonymous_function

例如，创建一个指向用于计算平方数的匿名函数的句柄 sqr，并使用其句柄调用该匿名函数。

sqr = @(n) n.^2;
x = sqr(3)
x =

     9

3.3 错误示范

function [y] = xy_plot(input,x)
% xy_plot receives the handle of a function
% and plots that function of x
y = input(x); plot(x,y,'r--');
xlabel('x'); ylabel('function(x)');
end

>> xy_plot(sin,0:0.01:2*pi)
错误使用 sin
输入参数的数目不足。

       调用参数的时候，如果该参数也是一个函数，这个时候直接将函数当成参数输入进去是不妥的，会直接报错，这个时候我们就需要句柄

>> 
xy_plot(@sin,0:0.01:2*pi)

ans =

  列 1 至 11

         0    0.0100    0.0200    0.0300    0.0400    0.0500    0.0600    0.0699    0.0799    0.0899    0.0998

  列 12 至 22

    0.1098    0.1197    0.1296    0.1395    0.1494    0.1593    0.1692    0.1790    0.1889    0.1987    0.2085

  列 23 至 33

    0.2182    0.2280    0.2377    0.2474    0.2571    0.2667    0.2764    0.2860    0.2955    0.3051    0.3146
...

3.4 integral() 数值积分

3.4.1 一级积分

\int_{0}^{2}\frac{1}{x^{3}-2x-5}dx

我们通过句柄该怎么去解决呢？

>> y = @(x) 1./(x.^3-2*x-5);
integral(y,0,2)

ans =

   -0.4605

3.4.2 integral2() 二级积分


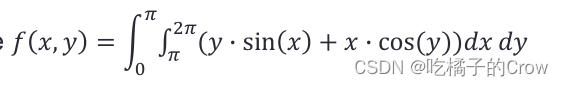
>> f = @(x,y) y.*sin(x)+x.*cos(y);
integral2(f,pi,2*pi,0,pi)

ans =

   -9.8696

3.4.3 integral3() 三级积分


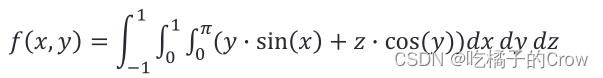
>> f = @(x,y,z) y.*sin(x)+z.*cos(y);
integral3(f,0,pi,0,1,-1,1)

ans =

    2.0000

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/963218.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

windows server 2019 安装sqlserver2012

windows server 2019 安装sqlserver2012

在安装前&#xff0c;应先关闭系统防火墙 双击exe 选择【全新SQL Server独立安装或向现有安装添加功能】选项 运行完成后&#xff0c;如无失败或警告&#xff0c;点击确定&#xff0c;如果出现警告&#xff0c;需要处理掉再继续执行 点击下一步 勾选接受许可&#xff0c;点击下…
阅读更多...
第一课：使用C++实现图片去水印

第一课：使用C++实现图片去水印

1.功能概述 实现图片去水印的方法有很多，下面提供一种基于OpenCV库的C++实现方法。主要思路是利用图像中不同水印区域之间的差异，进行区域提取、重构和合成，从而实现去除水印的效果。 2.具体实现 2.1.导入OpenCV库和头文件 #include <iostream> #include <o…
阅读更多...
图 —— 基础概念详解

图 —— 基础概念详解

文章目录 前言1. 顶点、边、阶2. 无向图、有向图、简单图、多重图、完全图&#x1f351; 无向图&#x1f351; 有向图&#x1f351; 简单图&#x1f351; 多重图&#x1f351; 完全图 3. 顶点的度、入度、出度4. 顶点之间的关系、路径、边5. 连通图、子图6. 生成树、生成森林7.…
阅读更多...
bazel远程构建(Remote Execution)

bazel远程构建(Remote Execution)

原理 既然 ActionResult 可以被不同的 Bazel 任务共享&#xff0c;说明 ActionResult 和 Action 在哪里执行并没有关系。因此&#xff0c;Bazel 在构建时&#xff0c;可以把 Action 发送给另一台服务器执行&#xff0c;对方执行完&#xff0c;向 CAS 上传 ActionResult&#x…
阅读更多...
ESLint 中的“ space-before-function-paren ”相关报错及其解决方案

ESLint 中的“ space-before-function-paren ”相关报错及其解决方案

ESLint 中的“ space-before-function-paren ”相关报错及其解决方案 出现的问题及其报错&#xff1a; 在 VScode 中&#xff0c;在使用带有 ESLint 工具的项目中&#xff0c;保存会发现报错&#xff0c;并且修改好代码格式后&#xff0c;保存会发现代码格式依然出现问题&…
阅读更多...
SpringBoot 整合 RabbitMQ

SpringBoot 整合 RabbitMQ

1. 创建 SpringBoot 工程 把版本改为 2.7.14 引入这两个依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId></dependency><dependency><groupId>org.springfr…
阅读更多...
在Mac 上安装flutter 遇到的问题

在Mac 上安装flutter 遇到的问题

准备工作 1、升级Macos系统为最新系统 2、安装最新的Xcode 3、电脑上面需要安装brew https://brew.sh/ 4、安装chrome浏览器(开发web用) 下载Flutter、配置Flutter环境变量、配置Flutter镜像 下载Flutter SDK https://docs.flutter.dev/release/archive?tabmacos 根据自己…
阅读更多...
吐槽丨为什么我依然喜欢用旧版UWP网易云音乐

吐槽丨为什么我依然喜欢用旧版UWP网易云音乐

实在忍不住吐槽一下 左侧&#xff1a;网易云音乐 真UWP版&#xff0c;UI间距宽松&#xff0c;页面清爽。 右侧&#xff1a;网易云音乐 假PC移植版&#xff0c;文字密集&#xff0c;显得杂乱无章&#xff0c;列表行距太窄。 左侧&#xff1a;真UWP版页面UI自适配&#xff0c;随…
阅读更多...
GEEMAP 基本操作（三）如何对图像进行 3D 叠加显示 （图像混合 blend）

GEEMAP 基本操作（三）如何对图像进行 3D 叠加显示 （图像混合 blend）

最近在 GIS 界有很多大神在讨论如何将图像下面混合一幅地形数据&#xff0c;这样看起来是 3D 的比较酷炫。 比如这样&#xff1a; 以上图片来自网络&#xff0c;是在专业软件中制作的。 GEEMAP 中是否可行呢&#xff1f;当然没问题&#xff0c;使用 blend 即可。下面的例子请笑…
阅读更多...
Flutter启动页

Flutter启动页

效果图 import dart:async; import package:flutter/cupertino.dart; import package:flutter/material.dart; import jumpPage.dart;class TransitPage extends StatefulWidget {const TransitPage({super.key});overrideState<TransitPage> createState() > _Trans…
阅读更多...
Gateway的服务网关

Gateway的服务网关

Gateway服务网关 Gateway网关是我们服务的守门神&#xff0c;所有微服务的统一入口。 网关的核心功能特性&#xff1a; 请求路由 权限控制 限流 架构如下&#xff1a; gateway使用 引入依赖 创建gateway服务&#xff0c;引入依赖 <!--网关--> <dependency>…
阅读更多...
PHP8的数组-PHP8知识详解

PHP8的数组-PHP8知识详解

今天开始学习数组&#xff0c; 本文主要讲了三点&#xff1a;什么是数组、php8中数组的改进、数组函数。 一、什么是数组 在PHP8中&#xff0c;数组是非常重要的数据类型。相对于其他的数据类型&#xff0c;数组更像一种结构&#xff0c;而这种结构可以储存一系列数值。 数组…
阅读更多...
ETLCloud制造业轻量级数据中台解决方案

ETLCloud制造业轻量级数据中台解决方案

制造业数据处理特点 制造业在业务发展过程中产生大量的业务交易数据以及设备运行过程中的状态数据&#xff0c;但是制造业有别于其他互联网或零售行业&#xff0c;其数据处理具有以下特点&#xff1a; 数据量不大&#xff0c;大部分业务系统的数据库表在1000W以下数据结构复杂…
阅读更多...
数据指标体系峰会——构建与应用

数据指标体系峰会——构建与应用

京东物流指标体系 流量指标体系 如何构建和应用指标体系 落地关键保障与举措 数据标准化&#xff0c;一致化比较困难。 火山引擎抖音集团指标分析与增长实践指南 实践Case 指标分析方法 策略假设方法论 《测出转化率》 lift模型 紧急度&#xff1a; 外部驱动&#xff…
阅读更多...
华为OD机试 - 敏感字段加密（Java 2023 B卷 100分）

华为OD机试 - 敏感字段加密（Java 2023 B卷 100分）

目录 专栏导读一、题目描述二、输入描述三、输出描述四、解题思路五、Java算法源码六、效果展示1、输入2、输出 华为OD机试 2023B卷题库疯狂收录中&#xff0c;刷题点这里 专栏导读 本专栏收录于《华为OD机试&#xff08;JAVA&#xff09;真题&#xff08;A卷B卷&#xff09;》…
阅读更多...
敦煌网、newegg店铺优化三大方法，测评补单原来可以这样做

敦煌网、newegg店铺优化三大方法，测评补单原来可以这样做

我们都知道敦煌网、newegg流量是一个店铺的血液&#xff0c;没有流量的支撑&#xff0c;其他也都将成为浮云。流量能够成为转化率的保证&#xff0c;如何让店铺拥有傲人的流量成为重要之重&#xff0c;店铺的流量又主要来源于以下几部分&#xff1a; 一、主要流量的来源 1.搜索…
阅读更多...
【探索SpringCloud】服务发现-Nacos服务端数据结构和模型

【探索SpringCloud】服务发现-Nacos服务端数据结构和模型

前言 上一文中&#xff0c;我们从官方的图示了解到Nacos的服务数据结构。但我关心的是&#xff0c;Nacos2.x不是重构了吗&#xff1f;怎么还是这种数据结构&#xff1f;我推测&#xff0c;必然是为了对Nacos1.x的兼容&#xff0c;实际存储应该不是这样的。于是&#xff0c;沿着…
阅读更多...
JAVA设计模式3：抽象工厂模式，这是一种创建型设计模式

JAVA设计模式3：抽象工厂模式，这是一种创建型设计模式

作者主页&#xff1a;Designer 小郑 作者简介&#xff1a;3年JAVA全栈开发经验&#xff0c;专注JAVA技术、系统定制、远程指导&#xff0c;致力于企业数字化转型&#xff0c;CSDN学院、蓝桥云课认证讲师。 主打方向&#xff1a;Vue、SpringBoot、微信小程序 本文讲解了 Java 设…
阅读更多...
嵌入式BL304可提供4路RS485/RS232口

嵌入式BL304可提供4路RS485/RS232口

BL304网关具有多功能的数据通信和处理设备&#xff0c;具有多种输入和输出接口&#xff0c;支持多种操作系统和应用程序&#xff0c;以及数据库连接。下面我们将详细介绍该产品的特点和功能。 设备提供了多路RS485/RS232接口、CAN口、网口、DI口、PWM口输出以及USB接口&#xf…
阅读更多...
算法面试-深度学习基础面试题整理（2023.8.29开始，每天下午持续更新....）

算法面试-深度学习基础面试题整理（2023.8.29开始，每天下午持续更新....）

一、无监督相关&#xff08;聚类、异常检测&#xff09; 1、常见的距离度量方法有哪些&#xff1f;写一下距离计算公式。 1&#xff09;连续数据的距离计算&#xff1a; 闵可夫斯基距离家族&#xff1a; 当p 1时&#xff0c;为曼哈顿距离&#xff1b;p 2时&#xff0c;为欧…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023