---

前言

图这种数据结构比树更加复杂，树形结构中的节点或者说数据之间有明显的层次关系，一个父节点可以有多个子节点，当然，一个子节点只能有唯一的父节点。但在图形结构中，节点之间可以有任意的关系，即任意两个数据都可能相关。

关于图的话，涉及的概念和术语比较多，需要反复记住。

图的基本概念：

重要知识点：

1. 顶点、边、阶

在图中，数据元素被称为 顶点，和在树中将数据元素称为节点是有区别的，用 v（Vertex）表示。不同的顶点之间的连线称为 边，用 e（Edge）表示。

图（Graph）是由顶点的 有穷非空 集合和顶点之间的连线（边）的集合组成。通常表示为 G=(V, E)，其中 G 表示一个图，V(G) 代表图 G 中的顶点集合，E(G) 代表图 G 中的边集合。

用 |V| 表示图 G 中顶点个数，也称为图 G 的阶。

用 |E| 表示图 G 中边的条数。

下图所示就是一个图，其中 A、B、C、D、E、F 是顶点。

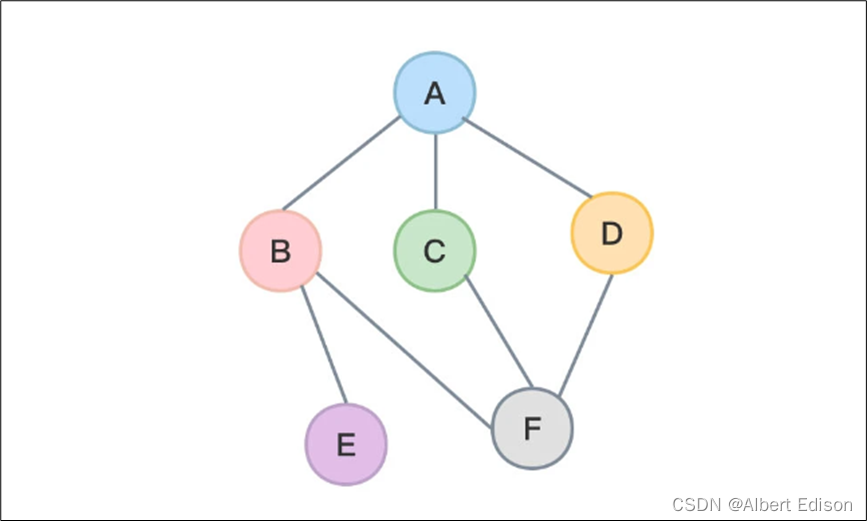
注意：图不可以为空，换句话说，顶点集合 V 不可以为空集。而边集合 E 可以为空，所以，下图 2 所示也是一个图。

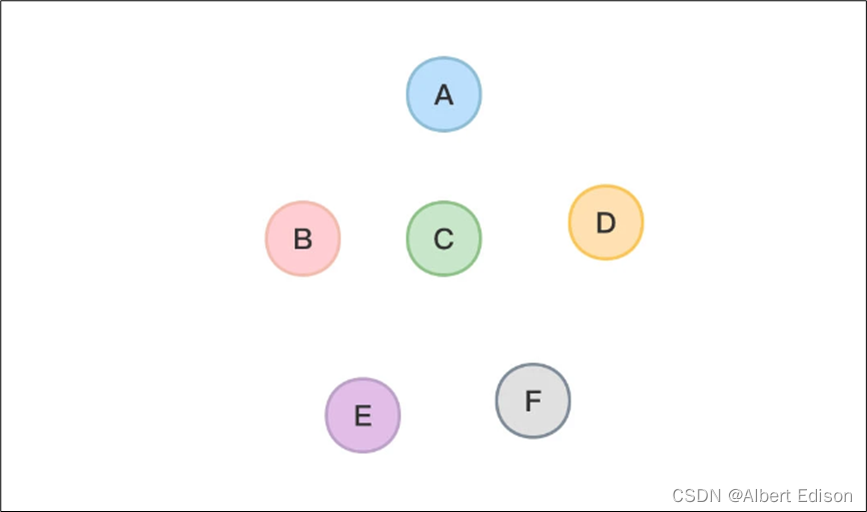
2. 无向图、有向图、简单图、多重图、完全图

🍑 无向图

上面介绍的图中的边是没有方向的，这种边就叫做 无向边（简称边）。

如果图中任意两个顶点之间的边都是无向边，则称该图为 无向图。

如下图所示：

对于无向图，只要两个顶点之间有一条边，则这两个顶点之间可以互相到达。

上图中，连接顶点 A 与 B 之间的边因为不存在方向问题，因此可以表示为无序对 (A,B) 或者 (B,A)。

注意：这里用的是 圆括号 表示无向边。

🍑 有向图

当然，从一个顶点到另外一个顶点的边也可以是有方向的，这种边称为 有向边，也称为 弧。

如果图中任意两个顶点之间的边都是有向边，则称该图为 有向图。

如下图所示：

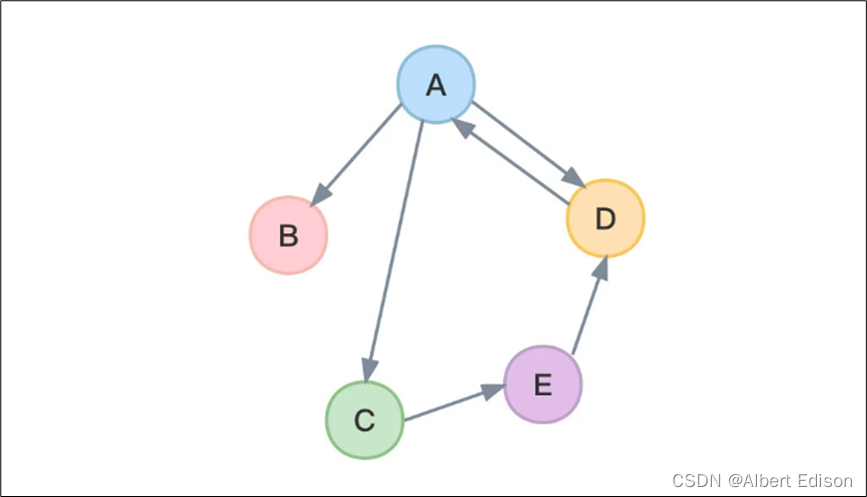
在上图中，顶点 A 到 B 之间存在一条有向边（从 A 指向 B 的箭头），这表示从顶点 A 可以到达顶点 B，但因为顶点 B 到顶点 A 之间并不存在有向边，所以从顶点 B 不可以到达顶点 A。

这里你可以设想一下 CSDN 用户之间的关系。你关注喜欢的用户之后，可以看到对方发的文章，但这并不等于人家也关注了你，如果对方没有关注你，那也看不到你发的文章。

顶点 A 到顶点 B 的有向边（箭头）就是弧。箭头开始的顶点 A 叫 弧尾，箭头指向的顶点 B 叫 弧头。这条弧可以用 <A,B> 表示，注意这里用的是 尖括号 表示有向边。另外还需要注意方向，不可以写成 <B,A>。

🍑 简单图

图中若不存在 顶点到其自身 的边，并且同一条边 不会重复 出现，这种图称为 简单图。

简单图分为：简单无向图和简单有向图。

🍑 多重图

图中某两个顶点之间的边数多于一条，或者顶点通过一条边和自己关联，这种图称为 多重图。

多重图分为：多重无向图和多重有向图。

如下如图 4 所示：

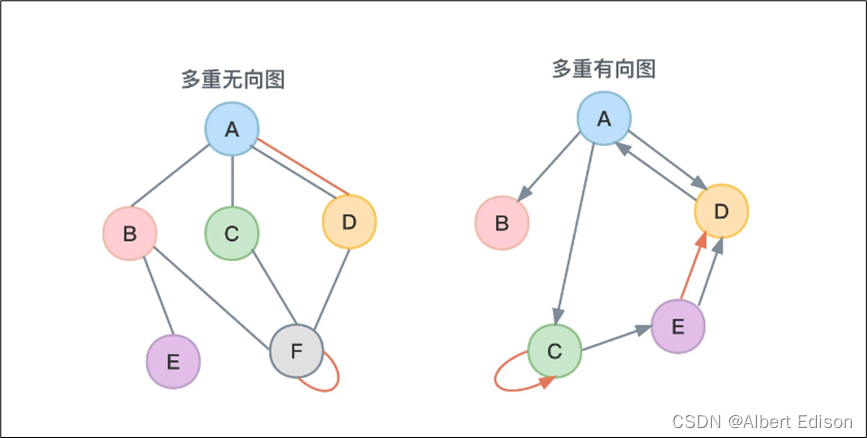
数据结构中所讨论的图都是 简单图，多重图不在讨论之中。基本上，绝大部分问题通过简单图都可以得到解决，比如 CSDN 中不需要自己加自己为好友，也不需要加同一个人多次好友。

🍑 完全图

在无向图中，如果任意两个顶点之间都存在边，则称该图为 无向完全图。

如下图所示：

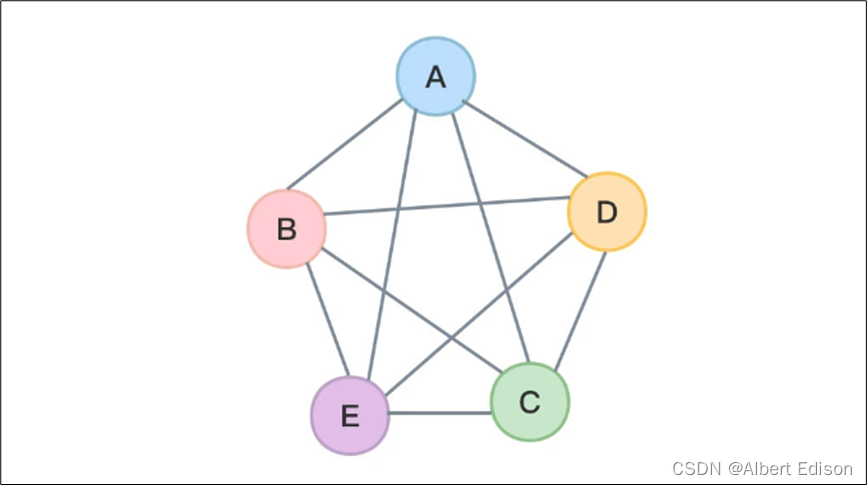
仔细观察后会发现，含有 n 个顶点的无向完全图有 $n(n-1)/2$ ​条边。

比上图中，一共有 5 个顶点，每个顶点有 4 条边，所以一共有 20 条边，但因为边是两两重复的，比如顶点 A 与顶点 B 的边也是顶点 B 与顶点 A 的边，所以边数要除以 2 也就是 $20/2=10$ 条边。

在有向图中，如果任意两个顶点之间都存在方向相反的两条弧，则称该图为 有向完全图。

如下图所示：

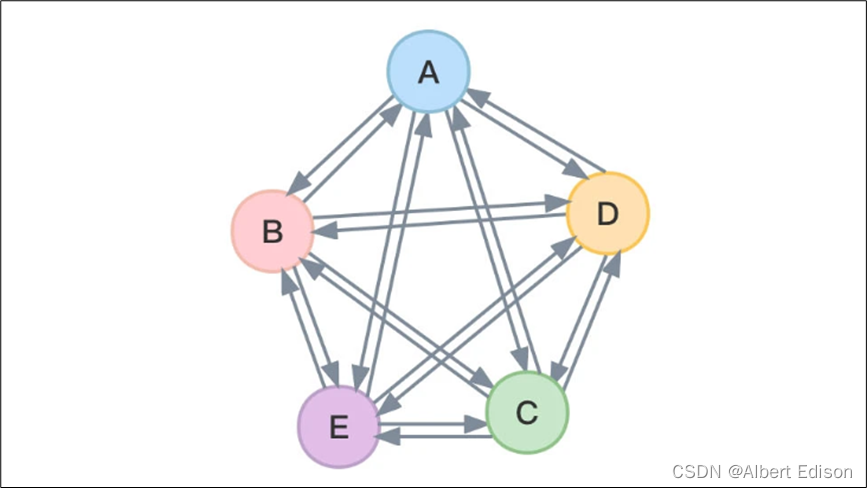
从上图中不难看出，含有 5 个顶点的有向完全图含有 20 条边，因此，含有 n 个顶点的有向完全图有 $n(n-1)$ 条边 。

有很少条边或者弧的图称为稀疏图，反之称为稠密图。这里稀疏和稠密都是相对而言的，并不是一个精确的数值。

3. 顶点的度、入度、出度

在无向图中，顶点 v 的度（Degree）是和 v 相关联的边的数目，记为 TD(v)。

比如下图中，顶点 A 的度为 3。

深入思考一下，无向图中，因为一条边可以给与这条边相连接的两个顶点分别提供 1 度，所以，无向图中所有顶点的度之和就应该是边数 * 2，即 2|E|。

在有向图中，以顶点 v 为终点（箭头指向 v）的有向边的数目称为顶点 v 的 入度（InDegree），记为 ID(v)。

以顶点 v 为起点的有向边的数目称为顶点 v 的 出度（OutDegree），记为 OD(v)。

所以，有向图中顶点 v 的度等于其 入度和出度之和，既 TD(v)=ID(v)+OD(v)。

比如下图中，顶点 A 的入度为 1，出度为 3，所以顶点 A 的度为 4。

有向图中，因为一条边可以给与这条边相连接的两个顶点分别提供 1 出度和 1 入度，所以 有向图所有顶点的入度之和与出度之和相等并且等于弧的数量。

4. 顶点之间的关系、路径、边

顶点 $v_m$​ 和顶点 $v_n$​ 的路径是一个顶点序列 $v_m,v_1,v_2,v_3,\dots \dots v_n$，该序列中的顶点属于图中的顶点集合。

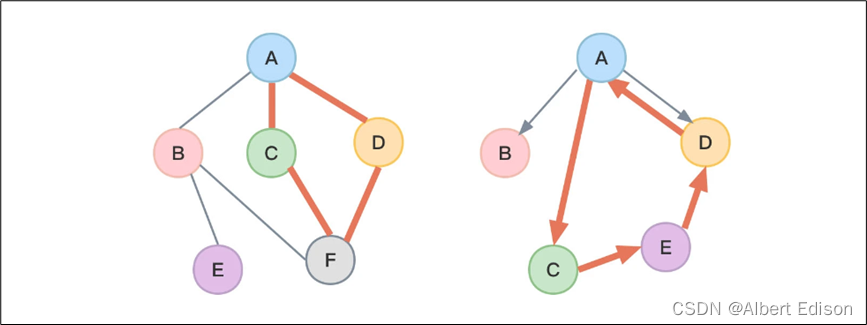
两个顶点的路径并不唯一，下图展示了无向图中从顶点 B 到 D 四种不同的路径，如粗线条所示（当然还有更多）。

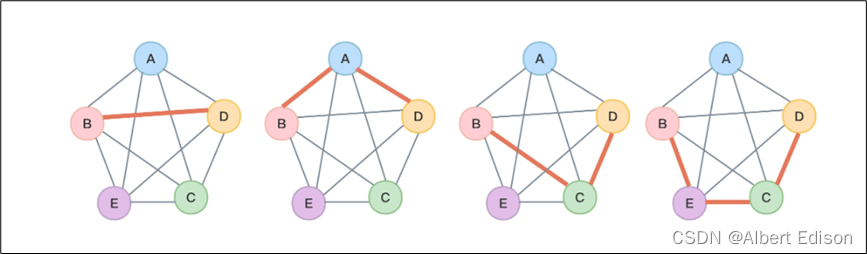
这里注意，对于有向图，路径也是有向的，下图展示了有向图中从顶点 A 到顶点 D 的两种不同路径。而对于 B 到 A 之间就不存在路径。

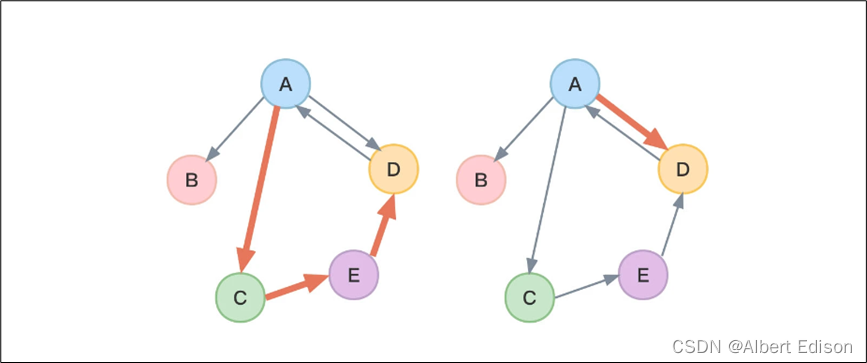
我们把第一个顶点和最后一个顶点相同的路径称为回路或环。如下图所示：

这么多的路径，其实也是涉及了一些专有名词的。

（1）简单路径

定义：在路径序列中顶点不重复出现的路径称为简单路径。

下图中，从顶点 A 到顶点 D 可以有多种不同路径，比如 A、B、A、D 这个路径，因为顶点 A 重复出现了，所以这就不是一个简单路径。

（2）简单回路 / 简单环

定义：除第一个顶点和最后一个顶点，其余顶点不重复出现的回路叫简单回路或简单环。

（3）路径长度

定义：路径上的边或弧的数目。

下图中的四幅图路径长度分别为 1、2、2、3

这幅图中的两幅图路径长度分别为 3、1。

（2）点到点的距离

定义：从顶点 $v_m$​ 到 $v_n$​ 的 最短路径 如果存在，则此路径的长度称为从顶点 $v_m$​ 到 $v_n$​ 的距离，如果 $v_m$​ 到 $v_n$​ 之间不存在路径，则称他们之间的距离为 无穷（∞）。

无向图中，若从顶点 $v_m$​ 到 $v_n$​ 之间有路径存在，则称 $v_m$​ 和 $v_n$​ 是 连通 的。

下图中，顶点 F 与其他顶点之间不连通，而除 F 外的其他顶点是彼此连通的。

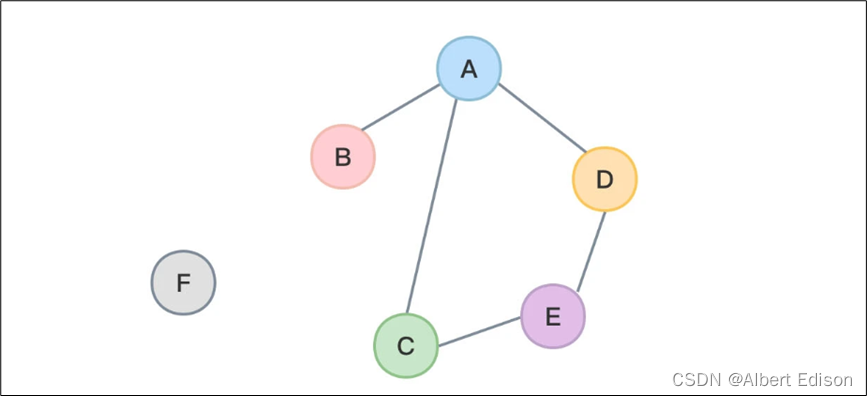
有向图中，若从顶点 $v_m$​ 到 $v_n$​ 之间和从顶点 $v_n$​ 到 $v_m$ 之间都有路径，则称这两个 顶点是强连通 的。

下图中，顶点 A 和 D 之间就是强连通的，而顶点 A 和 B 之间就不是强连通的，因为从 B 到 A 不存在路径。

有些图的边或弧有与其相关的数字，这种与图的边或者弧相关的数字叫 权（Weight）或者 权值。

这些权值可以表示从一个顶点到另一个顶点的距离、时间、票价等数据。

这种带权的图通常称为 带权图 或 网。

如下图所示：

5. 连通图、子图

局部的顶点、边了解完之后，我们再将视角放大，着眼于整张图。

如果 无向图 中任意两个顶点都是连通的，则称图为 连通图，否则称为 非连通图。

比如下图就是一个连通图。

因此得出几个结论：

• 对于具有 n 个顶点的无向图，如果是连通图，则最少要有 n-1 条边。
• 对于具有 n 个顶点的无向图，如果是非连通图，则最多只能有 $(n-1)(n-2)/2$ ​条边。

如何推出这个结论呢？

试想一下，含有 n 个顶点的无向完全图有 $n(n-1)/2$​ 条边，比如含有 5 个顶点的无向完全图有 10 条边，那么如果再增加进来一个顶点变成 6 个顶点，现在只要将这个新增加的顶点和任意其他顶点连线，就构成了连通图，所以 6 个顶点的非连通图最多只能有 10 条边。

如果 有向图 中任意一对顶点都是强连通的呢？那我们称此图为 强连通图。

如下图所示：

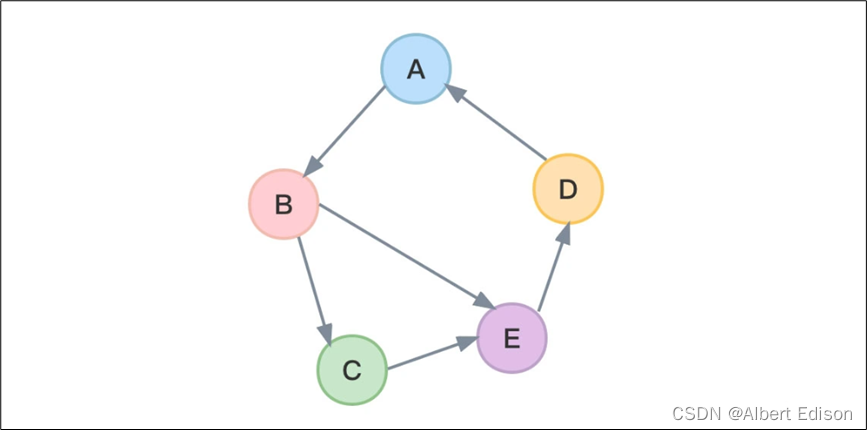
不难想象，对于有 n 个顶点的有向图，若是强连通图，则最少要有 n 条边以构成回路，如下图所示：

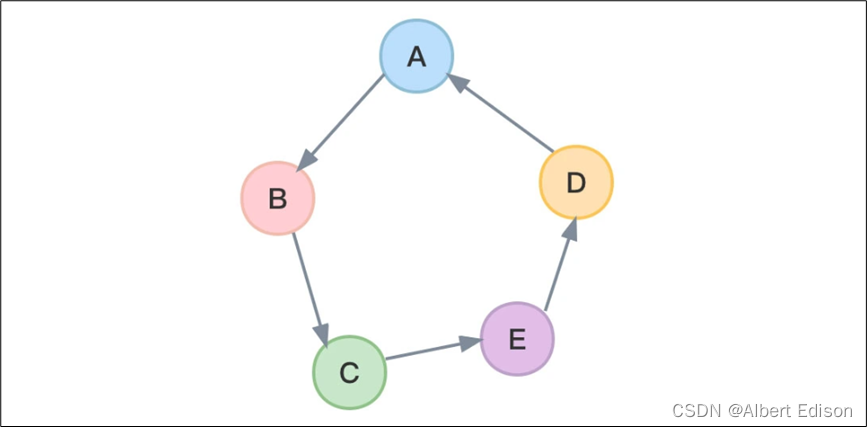
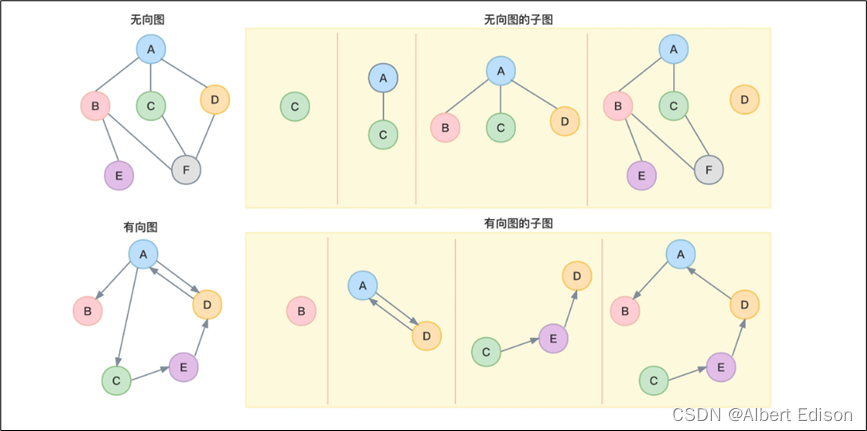
我们假设有图 1 和图 2 两个图，如果图 2 的顶点是图 1 的顶点的子集，并且图 2 的边是图 1 边的子集，则称图 2 是图 1 的 子图。

如果子图包含原图的所有顶点，则称该子图为原图的一个 生成子图。

下图所示，从第 2 个图开始的图都是第 1 个图的子图，而最后一个子图是原图的生成子图。

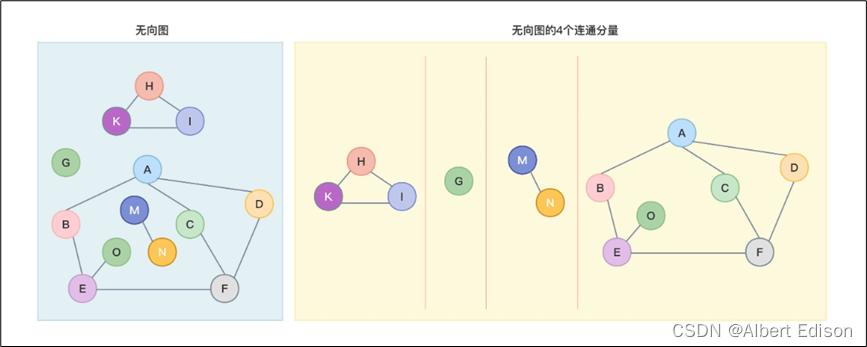
连通分量： 无向图中的极大连通子图称为连通分量。

换句话说，极大连通子图必须连通并且包含尽可能多的顶点和边，如下图所示：

举个例子，全国各个城市的地铁网，比如上海地铁网是全国地铁网的连通分量，深圳地铁网是全国地铁网的连通分量，诸如此类。

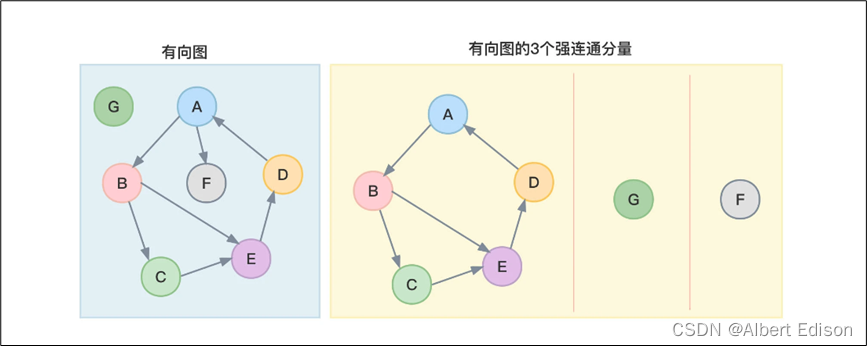
强连通分量： 有向图中的极大强连通子图称为强连通分量。这里的强连通意味着两两可达。如下图所示：

6. 生成树、生成森林

一个无向的连通图的生成树是包含图中全部顶点的一个极小的连通子图。

这里的极小指边尽可能要少，如下图所示：

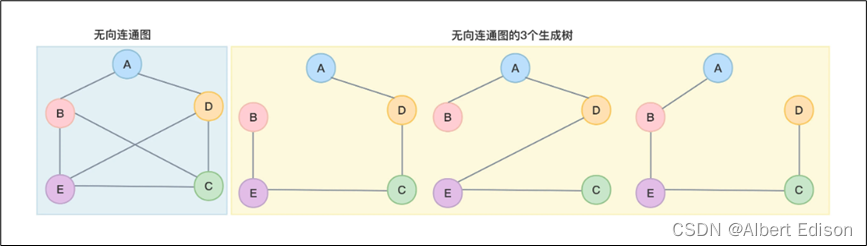
从上图可以看到，无向连通图的生成树可以有多个，生成树中如果有 n 个顶点，则必须有 n-1 条边。因为我们前面说过，n 个顶点的无向图，如果是连通图，则最少要有 n-1 条边。

话说回来：

• 如果一个无向图有 n 个顶点和小于 n-1 条边，则肯定是非连通图。
• 如果它多于 n-1 条边，则一定有回路（环）。
• 但有 n-1 条边的图不一定是生成树，因为生成树要求连通。

你可以想象一下通往各个城市的道路铺设场景，其中就可以用到生成树。

生成树 既可以保证各个城市之间彼此都可以到达，又可以保证铺设的道路尽可能少，而后可以在多个生成树中挑选最优的生成树方案。

比如如果想最节省成本，就可以把修每段路（边）的价格作为权值来计算总成本并最终挑选出总成本最少的修路方案。

如下图所示：

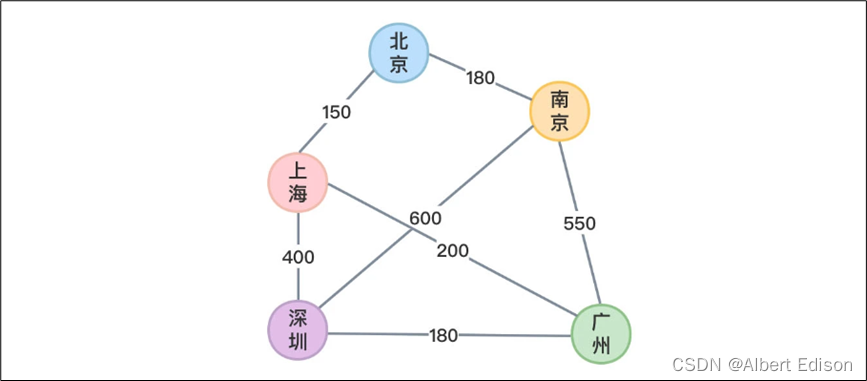
当图是带权图时，一条路径上所有边的权值之和称为 带权路径长度。

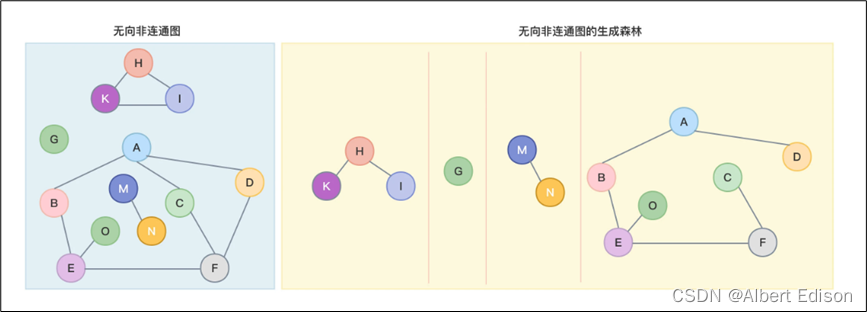
在无向非连通图中，连通分量的生成树构成了无向非连通图的生成森林。

如下图所示：

7. 树、有向树

在无向图中，树是连通且不存在回路的。

如下图所示：

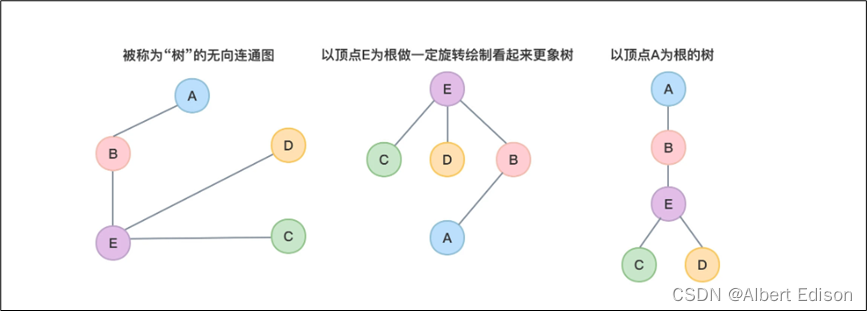
从上图可以看到，以 E、A 为根向下绘制看起来更像一棵树，当然，以任何其他顶点为根都是可以的。

注意：具有 n 个顶点的树，必然会有 n-1 条边，否则一定会是有回路的。

而在有向图中，一个顶点的入度为 0，其余顶点的入度均为 1，称为 有向树。

如下图所示：

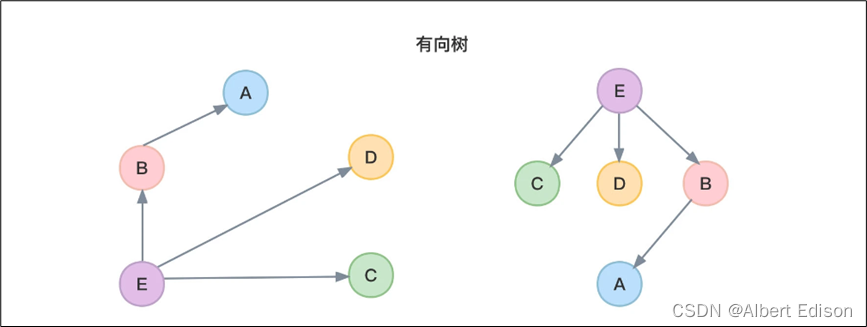
上图就是有向树，其中入度为 0 的顶点可以当做树的根，所以顶点 E 作为根。

8. 总结

关于图的概念不少，可以这篇文章的内容分成几个主题，把主题以及主题中一些比较重要的文字列举出来作为线索，然后重点理解和记忆。

主题一：顶点、边、阶

主题二：无向图、有向图、简单图、多重图、完全图

• 含有 n 个顶点的无向完全图有 $n(n-1)/2$​ 条边。
• 含有 n 个顶点的有向完全图有 $n(n-1)$ 条边。

主题三：顶点的度、入度、出度

• 无向图中所有顶点的度之和是边数 * 2，即 2|E|。
• 有向图所有顶点的 入度之和 与 出度之和 相等，并且等于 弧的数量。

主题四：顶点之间的关系、路径、边

主题五：连通图、子图

• 对于具有 n 个顶点的无向图，如果是连通图，则最少要有 $n-1$ 条边。
• 对于具有 n 个顶点的无向图，如果是非连通图，则最多只能有 $(n-1)(n-2)/2$​ 条边。
• 对于有 n 个顶点的有向图，若是强连通图，则最少要有 n 条边以构成回路。

主题六：生成树、生成森林

• 如果一个无向图有 n 个顶点和小于 n-1 条边，则肯定是非连通图。
• 如果它多于 n-1 条边，则一定有回路（环）。

主题七：树、有向树