向量空间是线性代数的重要研究对象，具有广泛的应用。

1 n维向量运算

    向量既有大小又有方向，如下表示：

m*n个数aij(i=1,2,...,m;j=1,2,...,n)排成m行n列的矩形数表

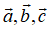
    若向量大小相当，方向相同则着两个向量相等

    n个数a1,a2,...,an组成的有序数组(a1,a2,...,an)称为n维向量，这n个数称为该向量的n个分量，分量全为实数的向量称为实向量，分量中有复数的向量称为复向量。列向量用字母αβ表示，行向量用αT,βT表示

    两个向量相等得满足以下条件：

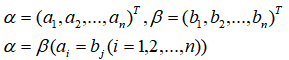
    分量全为0的向量称为0向量，记为0

    向量的线性运算和矩阵运算类似：

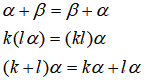
    我们可以用n维向量研究n元线性方程组：

    实数域上的全体n维向量，构成n维向量空间，记为R^n

2 向量组的线性相关性

    如果α1，α2，...，αm,β∈R^n，存在一组实数k1,k2,...,km，满足下面公式，则称β是向量组α1，α2，...，αm的一个线性组合，称k1,k2,...,km为组合系数

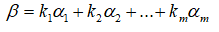
    下列公式中，当k1,k2,...,km是不全为0的实数，则称α1，α2，...，αm线性相关，否则称线性无关

    α1，α2，...，αm线性相关的充要条件是|A|=0

    矩阵A=(α1，α2，...，αm)的秩小于m则称α1，α2，...，αm线性相关，否则称线性无关

    α1，α2，...，αm线性相关的充要条件是至少有一个向量可以由其余m-1个向量线性表示

    设两个n维向量组A：α1，α2，...，αs和B：β1，β2，...，βt，若B中任一向量都可以由A中的向量线性表示，则称B可以由A线性表示

    若A能由B表示，B能由A表示，则称A与B等价，记作A~B

    如果向量组A：α1，α2，...，αs中有一个部分组B：αi1，αi2，...，αir，若B线性无关，再添加A中任意其他向量α，αi1，αi2，...，αir，α线性相关，则称B为A的一个极大线性无关组

    向量组A的极大线性无关组中所含向量的个数称为这个向量组的秩，记为r(A)

    若向量组A可由向量组B线性表示，则r(A)<=r(B)

    r(A+B)<=r(A)+r(B)，r(AB)<=min{r(A)，r(B)}

    矩阵的行向量组的秩称为A的行秩，矩阵的列向量组的秩称为A的列秩

    矩阵的初等行变换不改变列向量之间的线性关系，矩阵的初等列变换不改变行向量之间的线性关系

3 向量空间

    设V是n维向量空间R^n的一个非空子集，如果

• V对于向量加法是封闭的，即任意α，β∈V，有α+β∈V

• V对于数乘向量是封闭的，即任意α∈V，任意k∈R，有kα∈V

    则称集合V是一个向量空间

    设α1，α2，...，αr是向量空间V中的向量，满足

• α1，α2，...，αr线性无关

• V中任一向量都可以由α1，α2，...，αr线性表示

    则称α1，α2，...，αr为向量空间V的一个基，r称为向量空间V的维数，并称V为r维向量空间

    A：α1，α2，...，αn和B：β1，β2，...，βn是R的两组基，若(β1，β2，...，βn)=(α1，α2，...，αn)C，则称矩阵C为α到β的过渡矩阵

    设α=(a1,a2,...,an)^T，β=(b1,b2,...,bn)^T为R^n中的两个向量，记(α,β)称为α与β的内积，内积为实数，如下所示：

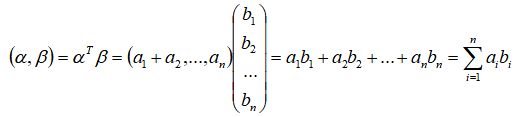
    向量α的长度称为α的模|α|，如下：

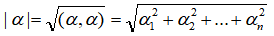
    长度为1的向量为单位向量

    设两个非零向量α，β∈R，规定α与β的夹角θ，如下：

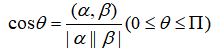
    如果(α,β)=0，称α与β正交，即两个非零向量正交的充要条件是θ=π/2

    若向量组α1，α2，...，αr两两正交，则α1，α2，...，αr称为正交向量组，正交向量组一定是线性无关的向量组

    若矩阵A满足以下条件则称为正交矩阵：

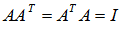
    正交矩阵有以下性质：