合并多个有序数组
- 题目描述
- 思想
- 代码实现
- 变形题目
题目描述
我们现在有多个已经有序的数组,我们知道每个有序数组的元素个数和总共的有序数组的个数,现在请设计一个算法来实现这多个有序数组的合并(合并成一个数组);
例如:
输入:[1,2,3,4,5,],[6,7],[8,9,10],[11,12,13,14];
输出:[1,2,3,4,5,6,7,8,9,10,11,12,13,14];
函数接口:
int* MulArrSort(int** nums, int Row, int* Col, int* returnSize)
{
//returnSize//返回合并的数组的元素个数
//Row有多少个有序数组
//Col数组,表示每个有序数组里面有多少个元素
}
思想
首先这道题的思路与合并两个有序数组 这道题的思路非常相似,都是每次从有序数组中选出较小的值出来,然后较小的值的下标往后挪动;
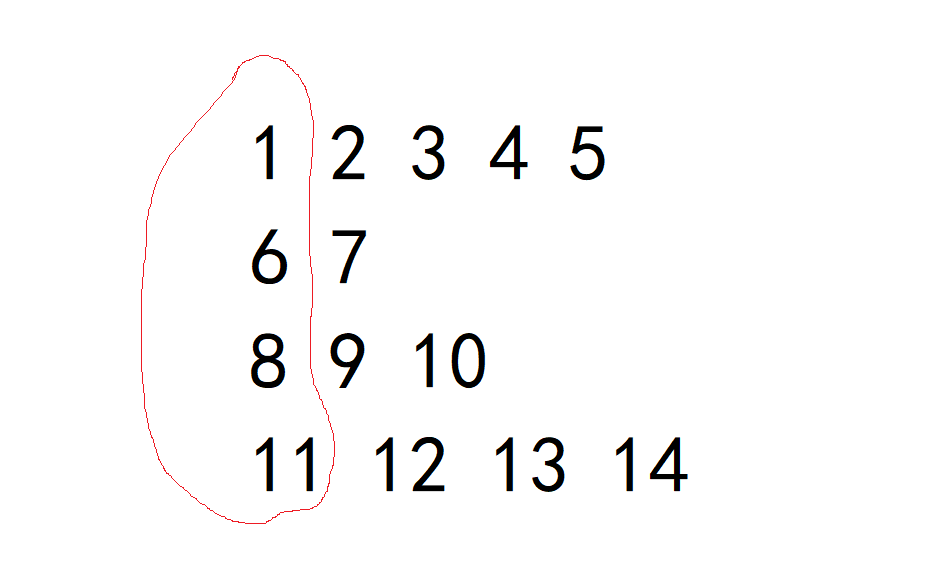
本题的思想也是如此,我们可以先将每个有序数组的最小值圈在一起,然后从这些最小值中选出较小的放入临时数组中,并且该较小值的下标也往后挪动一下:
比如:
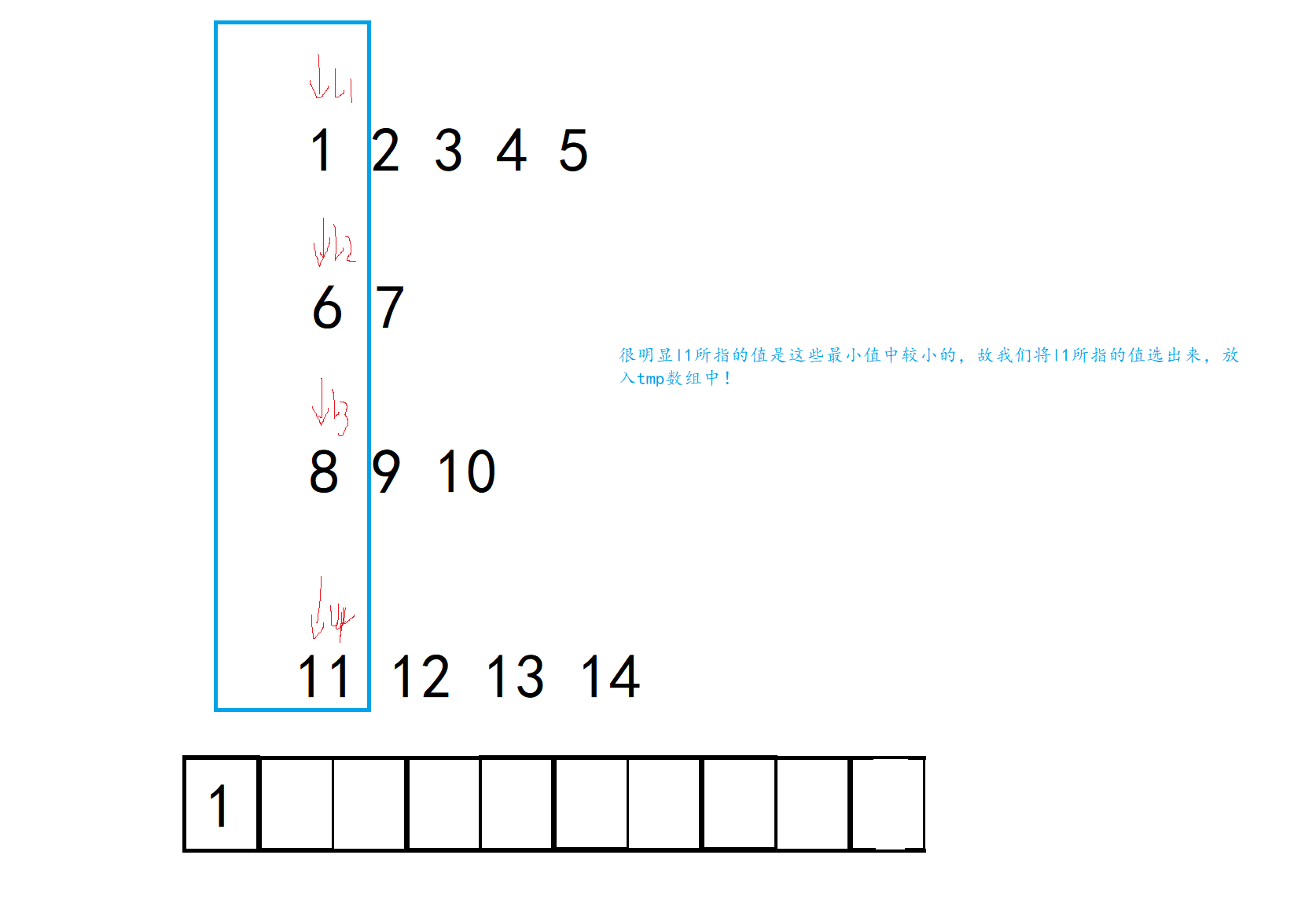
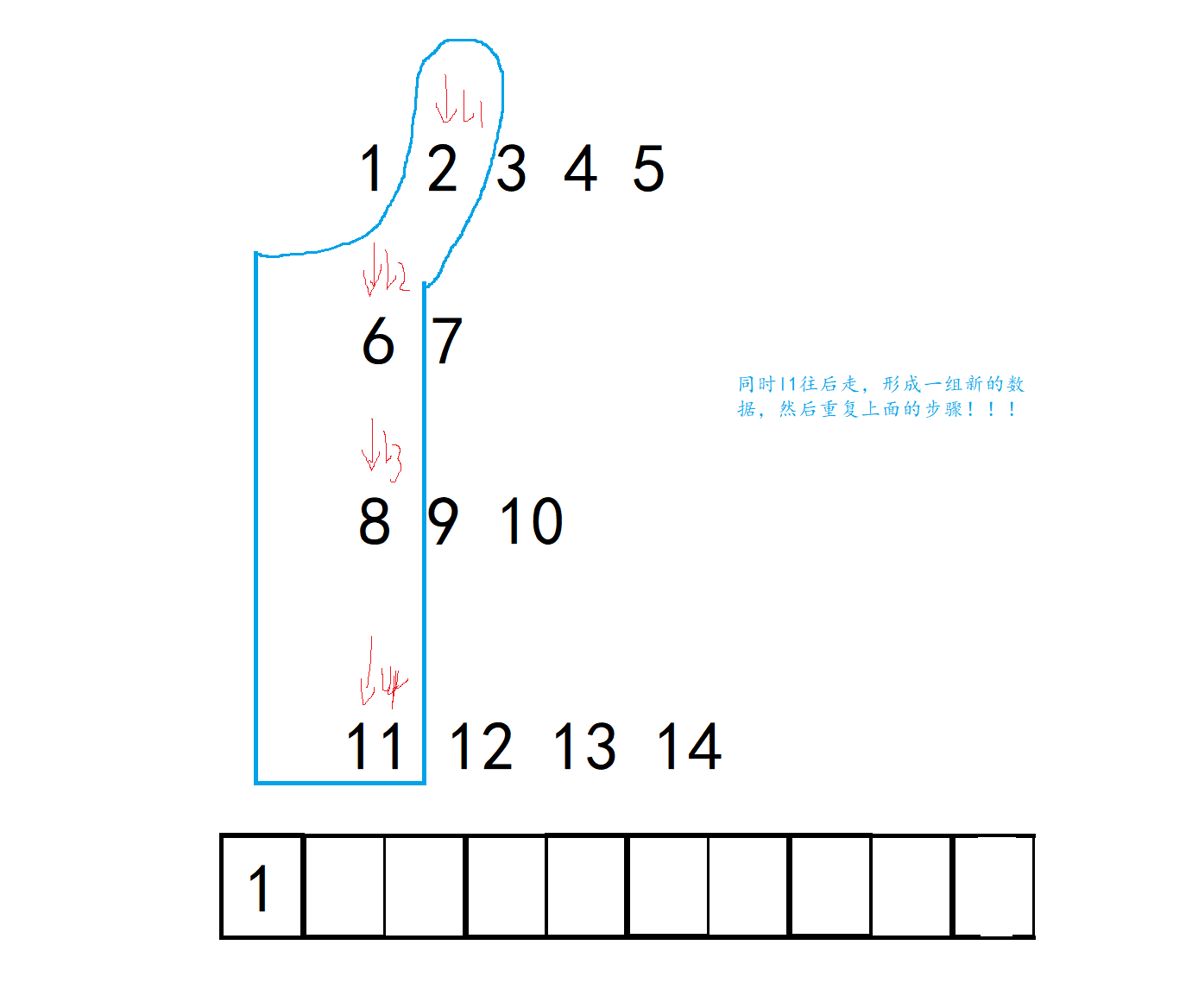
现在问题的关键是,我们怎么从这些数据中选出较小值,解决了这个问题本题也就轻松一半!
有两个方法
1、暴力选举
就对这些数一个一个遍历,选出最小值,时间复杂度O(K),时间开销太大了;
2、建立小堆
我们可以对这些数据进行建立小堆处理,然后堆顶元素就是这些数据中的较小值!时间复杂度也很乐观:O(logK);
为此我们选择第二种办法:
但是我们是直接对这些单一数据进行建堆吗?
当然不是,首先我们得想到,我们选出了较小值然后呢?如何往后走?是在那个有序数组里面往后走呢?
这些都是我们需要思考的问题,因此为了解决如何往后走的问题,我们需要一个结构体,这个结构体:包含当前元素的下标、当前数组的总元素个数、当前有序数组的数组名;

1、这就是我们建立的单个堆元素,我们以当前元素的大小来进行比较建立小堆;
2、然后每次选出堆顶元素所表示的值存储起来,同时更新堆顶元素,并重新利用向下调整算法调整小堆;
3、当某一个有序数组的元素被选完时,他就已经没有下个元素了,这时我们就需要将堆尾元素与堆顶元素进行替换,然后小堆的有效元素个数减1,而对于正常情况的话则对对顶元素进行正常替换即可;当小堆里面的有效元素没有了,就说明多个有序数组的合并也就完成了;
代码实现
struct Node
{
int index;//记录当前元素的位置
int* arr;//当前元素所在的数组
int len;//当前元素所在的数组的总长度
};
void Swap(struct Node* a, struct Node* b)
{
struct Node tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustDown(struct Node* Heap, int top, int end)
{
int parent = top;
int child = 2*parent+1;
while (child < end)
{
if (child + 1 < end && Heap[child + 1].arr[Heap[child + 1].index] < Heap[child].arr[Heap[child].index])
{
child++;
}
if (Heap[child].arr[Heap[child].index] >= Heap[parent].arr[Heap[parent].index])
break;
else
{
Swap(Heap+child,Heap+parent);
parent = child;
child = 2 * parent + 1;
}
}
}
int* MulArrSort(int** nums, int Row, int* Col, int* returnSize)
{
*returnSize = 0;
//计算合并数组的总元素个数
for (int i = 0; i < Row; i++)
{
*returnSize += Col[i];
}
//合并的总数组,用于存储合并的元素
int* ret = (int*)malloc(sizeof(int) * (*returnSize));
if (!ret)
exit(EXIT_FAILURE);
//1、建立初始堆数组
struct Node* Heap = (struct Node*)malloc(sizeof(struct Node) * (Row));
if (!Heap)
exit(EXIT_FAILURE);
int size = 0;//记录有效数组个数
for (int i = 0; i < Row; i++)
{
if (nums[i])//如果给的有序数组中有空数组,我们就不将其考虑进去建堆中
{
Heap[size].arr = nums[i];
Heap[size].index = 0;
Heap[size].len = Col[i];
size++;
}
}
int HeapSize = size;
//2、建立小堆
for (int top = (HeapSize - 1 - 1) / 2; top >= 0; top--)
{
AdjustDown(Heap,top,HeapSize);
}
int k = 0;//记录合并数组的下标
struct Node NextNode ={ 0 };
//3、开始选数
while (HeapSize)
{
ret[k++] = Heap[0].arr[Heap[0].index];//存入堆顶元素
NextNode = Heap[0];
NextNode.index++;//下标往后挪
//4、更新小堆
if (NextNode.index >= NextNode.len)//说明某一组有序数组已经选完了,这时候堆顶元素的跟新不需要特俗处理,由于当前有序数组已经遍历完毕,没有下一个元素,因此NextNode是无效数据,因此堆顶数据不能用NextNode更新,需要用堆尾元素更新,然后有效小堆元素个数--;
{
Swap(Heap+HeapSize-1,Heap);
HeapSize--;//有效元素--;
}
else//正常来到下一次的位置
{
Heap[0] = NextNode;//正常更新下一次位置
}
AdjustDown(Heap,0,HeapSize);
}
free(Heap);
return ret;
}
测试:
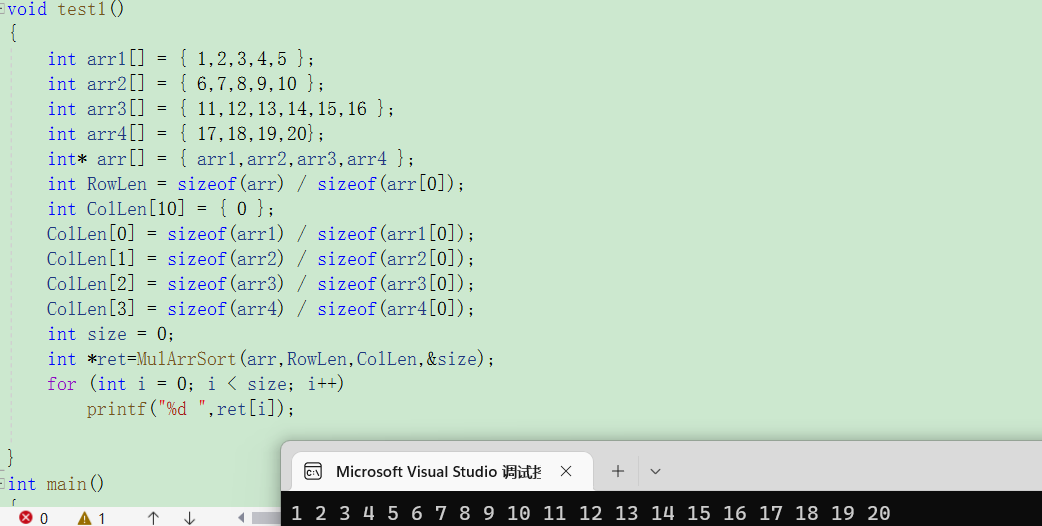
时间复杂度:O(K x n x logK)
空间复杂度:O(K)
变形题目
合并有序链表;
参考代码:
struct ListNode*BuyNode(int val)
{
struct ListNode*Node=(struct ListNode*)malloc(sizeof(struct ListNode));
Node->val=val;
Node->next=NULL;
return Node;
}
void Swap(struct ListNode**a,struct ListNode**b)
{
struct ListNode*tmp=*a;
*a=*b;
*b=tmp;
}
void AdjustDown(struct ListNode** lists,int top,int end)
{
int parent=top;
int child=2*top+1;
while(child<end)
{
if(child+1<end&&lists[child+1]->val<lists[child]->val)
child++;
if(lists[child]->val>=lists[parent]->val)
break;
else
{
Swap(lists+parent,lists+child);
parent=child;
child=2*parent+1;
}
}
}
struct ListNode* mergeKLists(struct ListNode** lists, int listsSize){
struct ListNode** Heap=(struct ListNode**)malloc(sizeof(struct ListNode*)*listsSize);
int size=0;
for(int i=0;i<listsSize;i++)
{
if(lists[i])
{
Heap[size++]=lists[i];
}
}
int HeapSize=size;
for(int top=(HeapSize-2)/2;top>=0;top--)
{
AdjustDown(Heap,top,HeapSize);
}
struct ListNode*dummyhead=(struct ListNode*)malloc(sizeof(struct ListNode));
dummyhead->next=NULL;
struct ListNode*cur=dummyhead;
while(HeapSize)
{
struct ListNode*next=Heap[0]->next;
struct ListNode*NewNode=BuyNode(Heap[0]->val);
cur->next=NewNode;
cur=NewNode;
if(next)
{
Heap[0]=next;
}
else
{
Swap(Heap,Heap+HeapSize-1);
HeapSize--;
}
AdjustDown(Heap,0,HeapSize);
}
struct ListNode*Head=dummyhead->next;
free(dummyhead);
free(Heap);
return Head;
}