1053.不相交的线

不会，这题和1143题代码一样，只不过题意不太能懂，难想，难想。

115.不同的子序列

难想，这种题就跟该画dp图去理解，太难了。

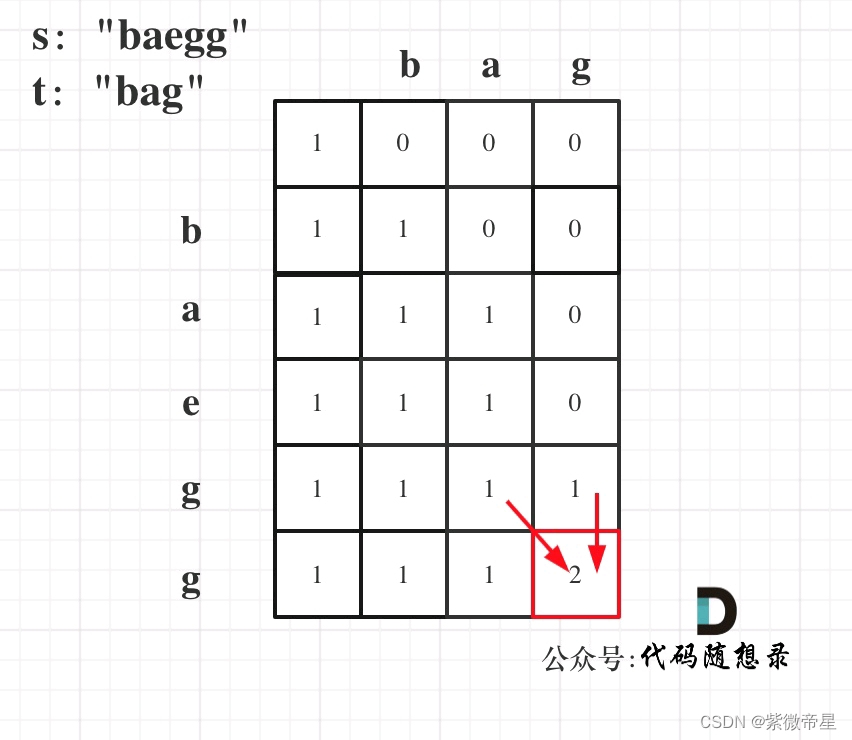
 跟着图去模拟一下，要不然真的答案都看不懂。

dp[i][j]：以s（i-1）为结尾的s子串的子序列中出现以t（j-1）为结尾的t子串的个数。

s[i - 1] 与 t[j - 1]相等，

s[i - 1] 与 t[j - 1] 不相等，

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。

class Solution {

    public int numDistinct(String s, String t) {

        int n1=s.length();

        int n2=t.length();

        int[][] dp=new int[n1+1][n2+1];

        for(int i=0;i<=n1;i++){

            dp[i][0]=1;

        }

        for(int i=1;i<=n1;i++){

            for(int j=1;j<=n2;j++){

                if(s.charAt(i-1)==t.charAt(j-1))

                dp[i][j]=dp[i-1][j-1]+dp[i-1][j];

                else

                dp[i][j]=dp[i-1][j];

            }

        }

        return dp[n1][n2];

 

    }

}