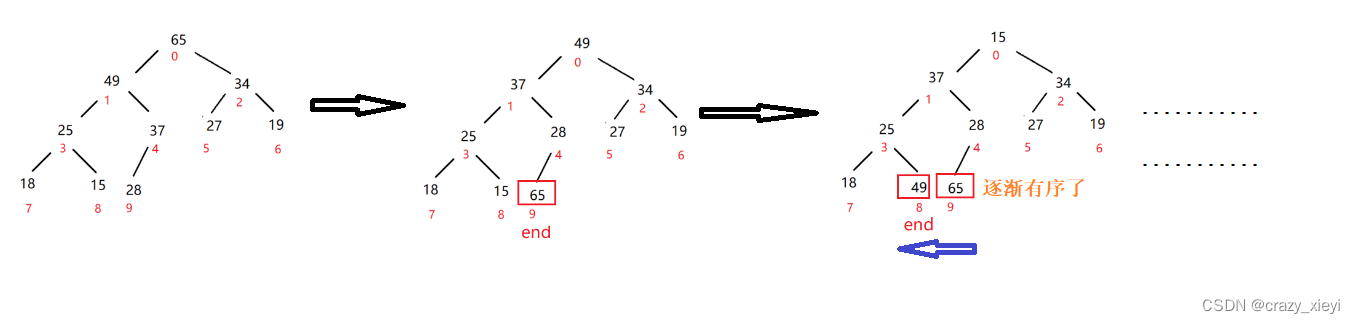
如果一个算法分阶段的工作,并且在每一个阶段都认为所做的决定是最好的,而不考虑将来的后果,这样的算法就叫做贪婪算法。贪婪算法只考虑当前局部的最优解,而不去考虑全局的情况,如果最终得到的结果是全局最优的,那么算法就是正确的,否则贪婪算法就只能得到一个次优解。如果不要求得到绝对的答案,那么使用贪婪算法得到次优解也是可以的,否则就需要使用更复杂的算法来得到准确结果。
举一个例子来说明贪婪算法不一定能够得到最优解:如果有12,10,5,1四种面值的纸币,要用最少的纸币来得到16元,如果使用贪婪算法,那么第一张选择12,还需要选择4张1元,这就需要5张纸币,但使用一张10,一张5以及一张1,就只需要三张纸币,这就说明贪婪算法并不总是成功的。
调度问题:
单处理器:
贪婪算法的一个例子是调度问题。现在有作业四份作业,完成这四份作业的时间分别为
,只有一个处理器,并且使用非预占调度:一旦开始一个作业,就必须把当前的作业运行完。如果要使完成作业的平均时间最短,应该如何调度?
| 作业 | 时间 |
| 15 | |
| 8 | |
| 3 | |
| 10 |
设表示处理的顺序,
表示作业的编号,那么处理完这四份作业所需要的总时间(即每个作业从处理器开始工作到完成该作业所花费的时间总和):
在第二个方程中,可以看到,等式后面的第一项是与作业处理顺序无关的,而要使最小,第二项就应该尽可能的大 ,那么由数学中的排序不等式可知,当
与
为同序时,也就是花费时间少的作业,处理的顺序也应该靠前,这样就能使第二项达到最大,从而使总时间达到最小。所以最优调度方案如图:

多处理器:
将问题推广到多处理器,假设有9份作业和3个处理器,那么最优调度方案其实与单处理器相似,只需要将9份作业从小到大排序,依次交由三个处理器处理即可(即使作业的份数不能整除处理器的个数,最优解依然是存在的):
| 工作 | 时间 |
| 3 | |
| 5 | |
| 6 | |
| 10 | |
| 11 | |
| 14 | |
| 15 | |
| 18 | |
| 20 |

但多个处理器在平均时间最优的情况下会有一个最终结束时间问题,如果交换7,8,9三份作业的位置,如下图:

那么可以看到,第二个方案的最终结束时间是38,而第一个方案是40。文中的这个例子存在一个最优的结束时间:

虽然对于单个处理器来说,完成自身所有任务的平均时间可能并没有前两个方案好,但是如果在实际中,我们需要等待这些任务处理完成后,再去进行下一步的操作,那么这时候最短的结束时间就是很有必要的。
Huffman编码:
贪婪算法的另一个例子就是文件压缩问题。
对于一个需要传输的文件,如果将文件中的所有字符都以ASCII码值编码,那么每个字符就需要8个bit,在文件比较大并且带宽较小的情况下,这个文件的传输将会非常的耗时。实际上,ASCII码值占8个bit是由于:标准的ASCII字符集由100个可打印字符及一些非打印字符组成,1个bit能表示两种情况,那么7个bit就能够表示128种不同的字符,再加上最高位作为奇偶校验位(校验数据传输是否正确),总共8个bit。
那么,如果一个文件中出现的不同字符总共有个,实际上每个字符就需要
个比特位来表示,在这种编码下,文件就被缩小了。
假设有一个文件,包含字符a、e、i、s、t,再加上一些空格和换行,并且有10个a、15个e、12个i、3个s、4个t、13个空格和1个换行,如图所示,这个文件就需要174位来表示:
| 字符 | 二进制编码 | 频率 | 总位数 |
| a | 000 | 10 | 30 |
| e | 001 | 15 | 45 |
| i | 010 | 12 | 36 |
| s | 011 | 3 | 9 |
| t | 100 | 4 | 12 |
| 空格 | 101 | 13 | 39 |
| 换行 | 110 | 1 | 3 |
| 总和 | 174 |
这个编码值可以使用一棵二叉树来表示:

在树中,左边表示0,右边表示1,每一个叶节点都代表一个字符,这样就可以保证编码无冲突,从根节点找到一个叶节点所经过的路径,就代表了这个叶节点字符的编码值。观察这幅图可以发现,换行符的父节点只有它一个孩子,所以可以将换行符放到它父节点的位置:
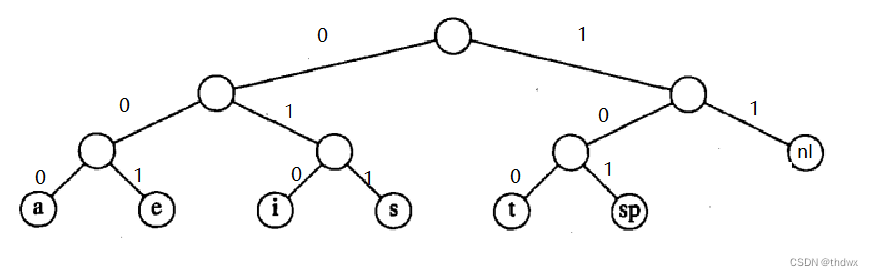 此时,换行符的编码就变成了11,则文件的总位数也变成了173,节省了一个bit的长度。上图中的树称为满树:所有的节点要么是叶子节点,要么有两个子节点。一些最优的编码总是具有这个性质,否则根据刚才的操作,我们总可以将只有一个孩子的节点向上移动一层 。
此时,换行符的编码就变成了11,则文件的总位数也变成了173,节省了一个bit的长度。上图中的树称为满树:所有的节点要么是叶子节点,要么有两个子节点。一些最优的编码总是具有这个性质,否则根据刚才的操作,我们总可以将只有一个孩子的节点向上移动一层 。
如果字符只放在叶子节点上,那么所有的字符就总是能被无歧义的编码。否则,假设o的编码是00,那么o的位置如图:

对于二进制码000001,我们就不能够知道它代表的是 ae 还是 oo或是其他,这样在编码时就会产生歧义,因为o是a的前缀编码。所以只有字符都放在叶子节点上,那么它们就不可能是任何其他字符的前缀编码,自然也就不会产生歧义。在文件中,e出现了最多次,那么如果我们将nl与e的位置互换,最后文件就只有159位,这就是Huffman算法的思想。
Huffman算法:
由Huffman算法生成的树就叫作Huffman树,得到的编码就是Huffman编码。Huffman算法的基本思想就是:对于一个文件中出现的所有字符,首先将其建立为一个森林,每个节点都存放字符本身以及字符出现的频率,然后选择其中频率最小的两个节点合并为一棵树,这棵树的频率为合并的两个节点频率树之和,然后将合并后的树放回森林,再找到两个频率最小的节点重复上述工作,直到最后只剩一棵树,就完成了Huffman编码。对于上述文件,建立Huffman树的具体过程如下:
首先建立初始森林:

选择频率最小的两个节点nl、s进行合并:
 然后重复操作:
然后重复操作:




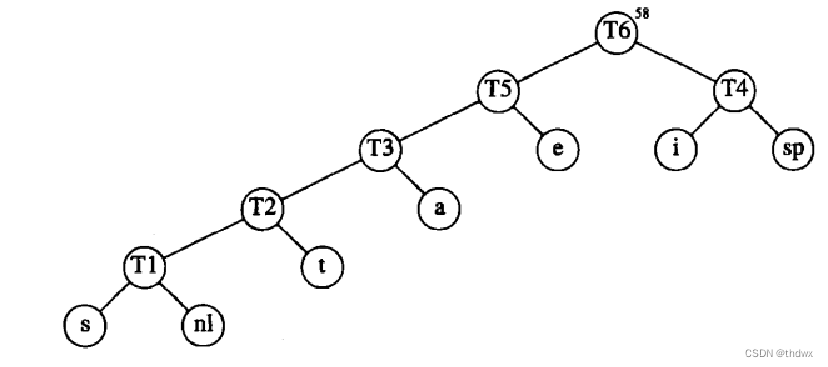
到这里就完成了Huffman树的建立。
Huffman树一定是一棵满树,因为如果不是满树,就一定存在一个只有一个孩子的节点,那么在合并时,就一定是只将森林中的一个节点与一个NULL进行合并,这与我们的操作过程是不符的;频率最小的节点一定是最深的,由数学归纳法知,在第一次合并时,显然结论是成立的。假设在T3次合并时结论也成立,那么在T5次合并时,如果e的频率小于T3的频率 ,并且e的频率要小于a或是T2的频率,那么在T3合并时,就会先将e进行合并,所以e的频率一定是大于比它更深的节点的。这样就可以使出现次数最多的字符的编码值是最短的,得到的编码就是最优的。
Huffman算法是一个贪婪算法是因为,在每次合并时,都是选择当前频率最小的两个节点进行合并,而并没有进行全局的考虑。如果使用堆来找到节点中频率最小的两个节点,那么Huffman算法的时间复杂度为,
为不同字符的个数。如果使用插入排序的话,时间复杂度就为
。将
个节点合并成一棵树需要线性时间,所以时间主要花费在排序上。
有两个细节需要考虑:
一是在传输压缩文件时,必须要传送编码信息,否则将无法解码,如果文件本身并不大,那么传输编码信息的代价可能超过了编码所带来的节省,这个时候不对文件进行压缩可能是一个更好的选择。
二是我们首先要直到文件中每个字符的频率,然后才能对它们使用Huffman算法,如果文件过大,那么就需要慎重考虑得到字符频率的算法。
Huffman算法代码如下:
typedef struct TreeNode {//树的节点,存放字符、频率以及子节点信息
char ch;
int times;
struct TreeNode* nodes[2];//向左为0,向右为1,正好以数组下标来表示
}TreeNode;
typedef struct HuffmanTree {//Huffman树,存放树的根节点
TreeNode* root;
}HuffmanTree;
void insertion_sort(TreeNode** p, int n) {//插入排序
for (int i = 1; i < n; i++) {
TreeNode* tmp = p[i];
int j;
for (j = i; j >= 1 && p[j - 1]->times < tmp->times; j--) {
p[j] = p[j - 1];
}
p[j] = tmp;
}
}
HuffmanTree* BuildHuffmanTree(TreeNode* arr, int n) {//建立一个Huffman树
HuffmanTree* p = (HuffmanTree*)malloc(sizeof(HuffmanTree));
p->root = NULL;
TreeNode** pt = (TreeNode**)malloc(sizeof(TreeNode*) * n);//建立一个森林
for (int i = 0; i < n; i++) {//将每个字符的数据都建立成一个树节点
TreeNode* ptt = (TreeNode*)malloc(sizeof(TreeNode));
ptt->ch = arr[i].ch;
ptt->nodes[0] = ptt->nodes[1] = NULL;
ptt->times = arr[i].times;
pt[i] = ptt;
}
insertion_sort(pt, n);//对森林进行排序,从大到小
for (int i = n - 1; i >= 1; i--) {
TreeNode* ptt = (TreeNode*)malloc(sizeof(TreeNode));
ptt->nodes[0] = pt[i];//选择最小的两个节点,并将它们合并
ptt->nodes[1] = pt[i-1];
ptt->times = pt[i]->times + pt[i - 1]->times;
pt[i - 1] = ptt;//每合并两个节点,森林中的节点数就会-1,所以将合并后的节点放在pt[i-1]位置,并重新排序
insertion_sort(pt, i);
}
p->root = pt[0];//当最后合并的节点放在pt[0]处时,说明森林中只剩一棵树,那么这个节点就是Huffman树的根节点
return p;//返回根节点
}
void print(TreeNode* p, char* buff, int i) {
if (p->nodes[0] == NULL && p->nodes[1] == NULL) {//如果左右子树都为空,说明这个就是字符所在的叶节点
buff[i] = 0;//那么buff就是该字符的编码值,所以直接输出
printf("%c %s\n", p->ch, buff);
return;
}
buff[i] = '0';//否则,向左走为0,向右走为1,深度也+1
print(p->nodes[0], buff, i + 1);
buff[i] = '1';
print(p->nodes[1], buff, i + 1);
}
void Print(HuffmanTree* tree) {//打印所有字符的编码值
char* buff = (char*)calloc(10, 1);//使用一个字符数组来存放当前层的前缀
if (tree->root == NULL) {//根节点为空说明没有编码
printf("Huffman树为空\n");
return;
}
int i = 0;//用来记录层数
print(tree->root, buff, i);
}测试代码:
void test() {
//输入10个小写字母以及它们的频次
#define NUM 10
TreeNode arr[NUM] = { 0 };//用来存放字符信息,以便生成森林
char str[10] = { 0 };
for (int i = 0; i < NUM; i++) {
scanf("%s %d", str, &arr[i].times);//直接以字符串形式读入,就不必再考虑空格换行符等情况
arr[i].ch = str[0];
}
HuffmanTree* p = BuildHuffmanTree(arr, NUM);
Print(p);
return;
}