在CNN模型的构建中,涉及到特别多的超参数,比如:学习率、训练次数、batchsize、各个卷积层的卷积核大小与卷积核数量(feature map数),全连接层的节点数等。直接选择的话,很难选到一组满意的参数,因此采用优化算法进行超参数优化,相比于多次尝试,优化算法会遵循自己的一套策略进行优化选择。
基于此思想,本文采用麻雀优化算法,对CNN上述9个超参数进行优化。
1,麻雀优化算法原理
麻雀优化是2020年提出来得,具体原理:原理点这里
2、麻雀优化CNN的原理
一般情况下进行参数的优化的时候,就是给CNN网络设一组超参数,然后训练并验证,取验证集精度最高的那个模型(这个模型就可以认为具有最优超参数)。其实优化算法也是这样,它们都是不断地产生新的超参数组合,然后用这组超参数建立CNN网络,训练并验证。只不过,优化算法是有自己的学习规律。我们对CNN超参数进行优化,也就是让SSA一直有去找能够让验证集满足精度最大化的那一组超参数。
3、代码实现:
数据采用多输入单输出,在我的excel表中,最后一列是输出,前几列都是输入,当然你也可以换成多输出格式,这样把自己的input和output写对即可。
3.1 CNN模型
clc;clear;close all;rng(0)
%% 数据的提取
data=xlsread('data.xlsx');
input=data(:,1:end-1);%x
output=data(:,end);%y
%% 数据处理
n=randperm(size(input,1));
m=round(size(input,1)*0.7);%随机70%作为训练集 其余30%作为测试集
train_x=input(n(1:m),:);
train_y=output(n(1:m),:);
test_x=input(n(m+1:end),:);
test_y=output(n(m+1:end),:);
% 归一化或者标准化
method=@mapminmax;
% method=@mapstd;
[train_x,train_ps]=method(train_x');
test_x=method('apply',test_x',train_ps);
[train_y,output_ps]=method(train_y');
test_y=method('apply',test_y',output_ps);
feature=size(train_x,1);
num_train=size(train_x,2);
num_test=size(test_x,2);
trainD=reshape(train_x,[feature,1,1,num_train]);
testD=reshape(test_x,[feature,1,1,num_test]);
targetD = train_y';
targetD_test = test_y';
%%
layers = [
imageInputLayer([size(trainD,1) size(trainD,2) size(trainD,3)]) % 输入
convolution2dLayer(3,4,'Stride',1,'Padding','same')%核3*1 数量4 步长1 填充为same
reluLayer%relu激活
convolution2dLayer(3,8,'Stride',1,'Padding','same')%核3*1 数量8 步长1 填充为same
reluLayer%relu激活
fullyConnectedLayer(20) % 全连接层1 20个神经元
reluLayer
fullyConnectedLayer(20) % 全连接层2 20个神经元
reluLayer
fullyConnectedLayer(size(targetD,2)) %输出层
regressionLayer];
options = trainingOptions('adam', ...
'ExecutionEnvironment','cpu', ...
'MaxEpochs',30, ...
'MiniBatchSize',16, ...
'InitialLearnRate',0.01, ...
'GradientThreshold',1, ...
'shuffle','every-epoch',...
'Verbose',false);
train_again=1;% 为1就代码重新训练模型,为0就是调用训练好的网络
if train_again==1
[net,traininfo] = trainNetwork(trainD,targetD,layers,options);
save result/cnn_net net traininfo
else
load result/cnn_net
end
figure;
plot(traininfo.TrainingLoss,'b')
hold on;grid on
ylabel('损失')
xlabel('训练次数')
title('CNN')
%% 结果评价
YPred = predict(net,testD);YPred=double(YPred);
% 反归一化
predict_value=method('reverse',YPred',output_ps);predict_value=double(predict_value);
true_value=method('reverse',targetD_test',output_ps);true_value=double(true_value);
save result/cnn_result predict_value true_value
%%
figure
plot(true_value,'-*','linewidth',3)
hold on
plot(predict_value,'-s','linewidth',3)
legend('实际值','预测值')
title('CNN')
grid on
result(true_value,predict_value)
损失曲线与测试集结果如图所示:


结果如下:
R-square决定系数(R2):0.79945
平均相对误差(MPE):0.20031
平均绝对百分误差(MAPE):20.0306%
平均绝对误差(MAE):0.32544
根均方差(RMSE):0.47113
3.2 SSA优化CNN
clc;clear;close all;format compact;rng(0)
%% 数据的提取
data=xlsread('data.xlsx');
input=data(:,1:end-1);%x
output=data(:,end);%y
%% 数据处理
n=randperm(size(input,1));
m=round(size(input,1)*0.7);%随机70%作为训练集 其余30%作为测试集
train_x=input(n(1:m),:);
train_y=output(n(1:m),:);
test_x=input(n(m+1:end),:);
test_y=output(n(m+1:end),:);
% 归一化或者标准化
method=@mapminmax;
% method=@mapstd;
[train_x,train_ps]=method(train_x');
test_x=method('apply',test_x',train_ps);
[train_y,output_ps]=method(train_y');
test_y=method('apply',test_y',output_ps);
feature=size(train_x,1);
num_train=size(train_x,2);
num_test=size(test_x,2);
trainD=reshape(train_x,[feature,1,1,num_train]);
testD=reshape(test_x,[feature,1,1,num_test]);
targetD = train_y';
targetD_test = test_y';
%% SSA优化CNN的超参数
%一共有9个参数需要优化,分别是学习率、迭代次数、batchsize、第一层卷积层的核大小、和数量、第2层卷积层的核大小、和数量,以及两个全连接层的神经元数量
optimaztion=1;
if optimaztion==1
[x,trace]=ssa_cnn(trainD,targetD,testD,targetD_test);
save result/ssa_result x trace
else
load result/ssa_result
end
%%
figure
plot(trace)
title('适应度曲线')
xlabel('优化次数')
ylabel('适应度值')
disp('优化后的各超参数')
lr=x(1)%学习率
iter=x(2)%迭代次数
minibatch=x(3)%batchsize
kernel1_size=x(4)
kernel1_num=x(5)%第一层卷积层的核大小
kernel2_size=x(6)
kernel2_num=x(7)%第2层卷积层的核大小
fc1_num=x(8)
fc2_num=x(9)%两个全连接层的神经元数量
%% 利用寻优得到参数重新训练CNN与预测
rng(0)
layers = [
imageInputLayer([size(trainD,1) size(trainD,2) size(trainD,3)])
convolution2dLayer(kernel1_size,kernel1_num,'Stride',1,'Padding','same')
reluLayer
convolution2dLayer(kernel2_size,kernel2_num,'Stride',1,'Padding','same')
reluLayer
fullyConnectedLayer(fc1_num)
reluLayer
fullyConnectedLayer(fc2_num)
reluLayer
fullyConnectedLayer(size(targetD,2))
regressionLayer];
options = trainingOptions('adam', ...
'ExecutionEnvironment','cpu', ...
'MaxEpochs',iter, ...
'MiniBatchSize',minibatch, ...
'InitialLearnRate',lr, ...
'GradientThreshold',1, ...
'Verbose',false);
train_again=1;% 为1就重新训练模型,为0就是调用训练好的网络 load options_data1600.mat ,changed!must retrain train_again=0;% 为1就重新训练模型,为0就是调用训练好的网络
if train_again==1
[net,traininfo] = trainNetwork(trainD,targetD,layers,options);
save result/ssacnn_net net traininfo
else
load result/ssacnn_net
end
figure;
plot(traininfo.TrainingLoss,'b')
hold on;grid on
ylabel('损失')
xlabel('训练次数')
title('SSA-CNN')
%% 结果评价
YPred = predict(net,testD);YPred=double(YPred);
% 反归一化
predict_value=method('reverse',YPred',output_ps);predict_value=double(predict_value);
true_value=method('reverse',targetD_test',output_ps);true_value=double(true_value);
save result/ssa_cnn_result predict_value true_value
%%
figure
plot(true_value,'-*','linewidth',3)
hold on
plot(predict_value,'-s','linewidth',3)
legend('实际值','预测值')
title('SSA-CNN')
grid on
result(true_value,predict_value)
以最小化测试集真实值与预测值的均方差为适应度函数,目的就是找到一组超参数,使得网络均方误差最低。所以适应度曲线是一条下降的曲线


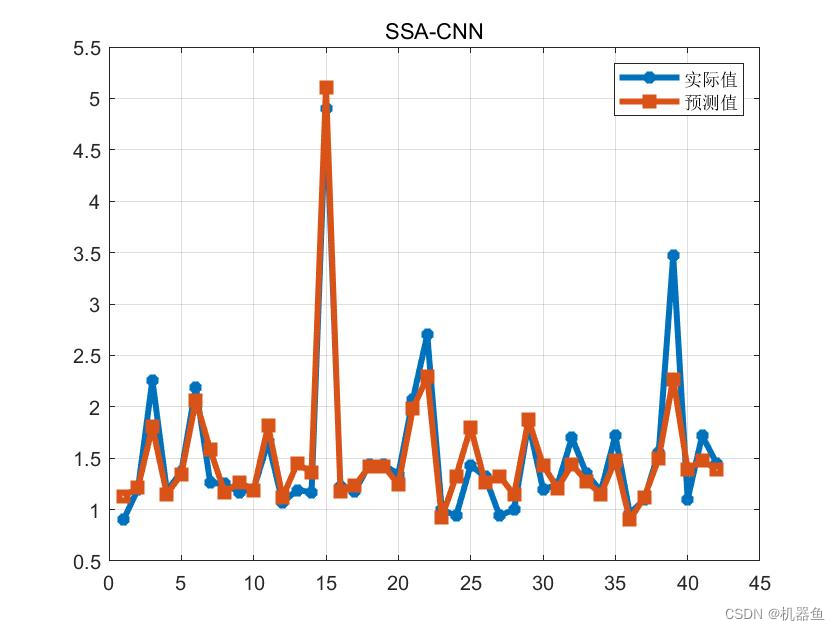
结果如下:
R-square决定系数(R2):0.86547
平均相对误差(MPE):0.114
平均绝对百分误差(MAPE):11.3997%
平均绝对误差(MAE):0.17238
根均方差(RMSE):0.26745
可以看到测试集指标具有明显提升。
4.代码
代码见评论区,还有更多哦
1.MATLAB麻雀优化CNN超参数回归