系列文章目录

数据结构之堆_crazy_xieyi的博客-CSDN博客

文章目录

前言
一、Top-k问题
1.前K个最小数（第k个最小数）
2.前K个最大数（第K个最大数）
二、堆排序
- 1.从小到大排序（建大根堆）
- 2.从大到小排序（建小跟堆）

前言

JDK1.8 中的 PriorityQueue底层使用了堆的数据结构，用堆作为底层结构 封装了优先级队列。

建堆（向下调整）的时间复杂度O(N)：

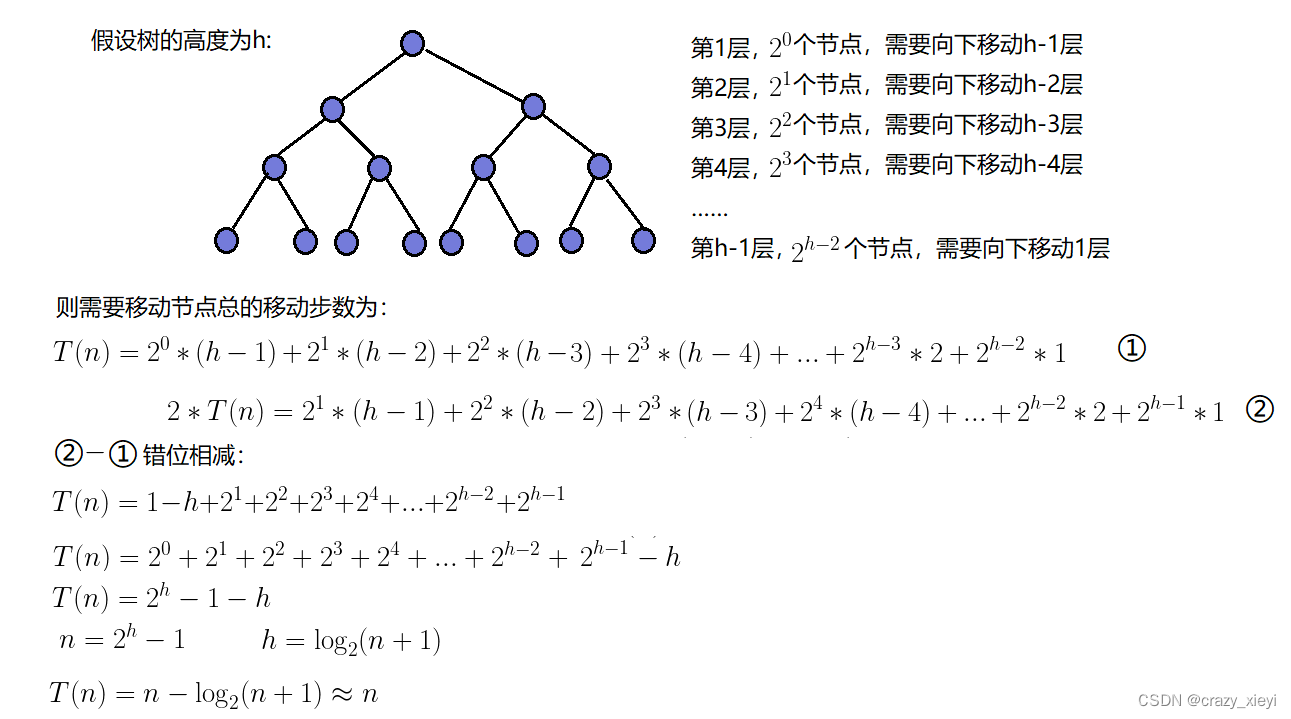
向上调整建堆的时间复杂度为O(nlogn).

一、Top-k问题

示例：在给定的一个数组中求前K个最小的数

第一种思路：把给定的数组直接进行排序，然后前K个一定是最小的数；

 public int[] getLeastNumbers(int[] arr, int k) {
           Arrays.sort(arr);
            int[] str = new int[k];
            for (int i = 0; i < k; i++) {
                 str[i] = arr[i];
            }
            return str;
    }

显然这种方式是不可取的，如果数据量非常大，排序就不太可取了(可能数据都

不能一下子全部加载到内存中 ) 。最佳的方式就是用堆来解决。

第二种思路：把整个数组整体建小根堆，然后依次弹出K个堆顶的数据。

public static int[] smallestK(int[] arr, int k) {
        //1. 建立一个小根堆
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        //2、取出数组当中的每个元素，存放到小跟堆当中
        for (int i = 0; i < arr.length; i++) {
            minHeap.offer(arr[i]);
        }
        //3.弹出K个元素，存放到数组当中,返回即可
        int[] tmp = new int[k];
        for (int i = 0; i < k; i++) {
            tmp[i] = minHeap.poll();
        }
        return tmp;
    }

但是你会发现，这种方式虽然可以，但是时间复杂度比较高，还是不可取得。整体建堆的时间复杂度为o(n),然后弹出K次时间复杂度为Klogn，则总体时间复杂度为 O(N + Klogn);

第三种思路：

1. 用数据集合中前 K个元素来建堆： 前 k 个最大的元素，则建小堆；前 k 个最小的元素，则建大堆。

2. 用剩余的 N-K 个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余 N-K 个元素依次与堆顶元素比完之后，堆中剩余的 K 个元素就是所求的前 K 个最小或者最大的元素。

下面还是用上面求前K个最小的数为例：

        public int[] getLeastNumbers(int[] arr, int k) {
           PriorityQueue<Integer> minHeap = new PriorityQueue<>(new Comparator<Integer>() {
                @Override
                public int compare(Integer o1, Integer o2) {
                    return o2.compareTo(o1);
                }
            });
            if (arr == null || k == 0)return new int[0];
            //用K个元素，先建立一个大根堆
            for (int i = 0; i < k; i++) {
                minHeap.offer(arr[i]);
            }
            //剩余元素与堆元素进行比较
            for (int i = k; i < arr.length; i++) {
                if (arr[i] < minHeap.peek()){
                    minHeap.poll();
                    minHeap.offer(arr[i]);
                }
            }
            //返回前K个元素
            int[] str = new int[k];
            for (int i = 0; i < k; i++) {
                str[i] = minHeap.poll();
            }
            return str;
        }

此时时间复杂度为：k + (n-k)logk ,约等于nlogk。

那么现在有一个小问题，就是第K个最小的怎么求？

其实这一点非常简单，求第K个最小的，只需要弹出一次就好了，因为此时是大跟堆，那么第K个最小的肯定就是堆顶的元素。

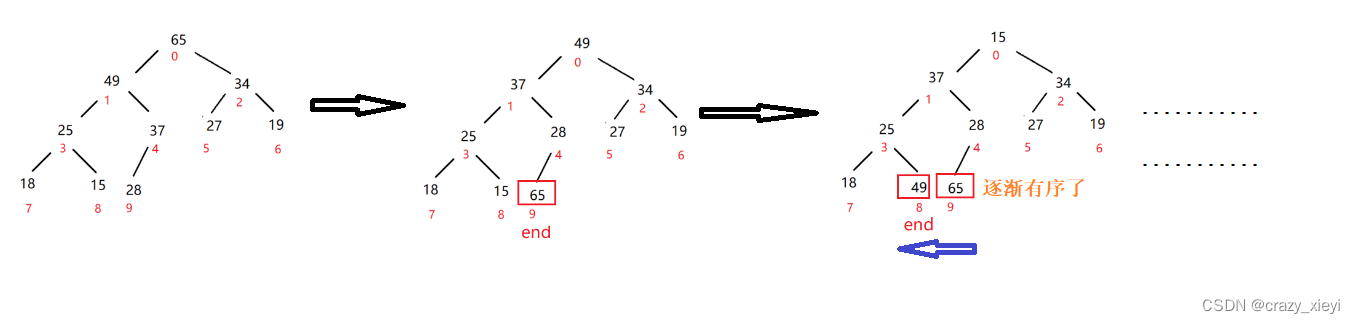
二、堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

    /**
     * 时间复杂度：
     *  O(n) + O(n*logn) 约等于 O(nlogn)
     *  空间复杂度：O(1)
     */
    public void heapSort() {
        //1.建立大根堆 O(n)
        createHeap();
        //2.然后排序
        int end = usedSize-1;
        while (end > 0) {
            int tmp = elem[0];
            elem[0] = elem[end];
            elem[end] = tmp;
            shiftDown(0,end);
            end--;
        }
    }

    private void shiftDown(int root,int len) {
        int child = root*2 + 1;
        while (elem[child] > elem[root]){
            if (child+1 < len && elem[child] < elem[child+1]){
                child++;
            }
            if (elem[child] > elem[root]){
                int temp = elem[child];
                elem[child] = elem[root];
                elem[root] = temp;
                child = root;
                root = (child-1)/2;
            }else {
                break;
            }
        }
    }