文章目录

1.二叉树层序遍历

2.完全二叉树的判断

文章内容

1.二叉树层序遍历

        二叉树的层序遍历需要一个队列来帮助实现。

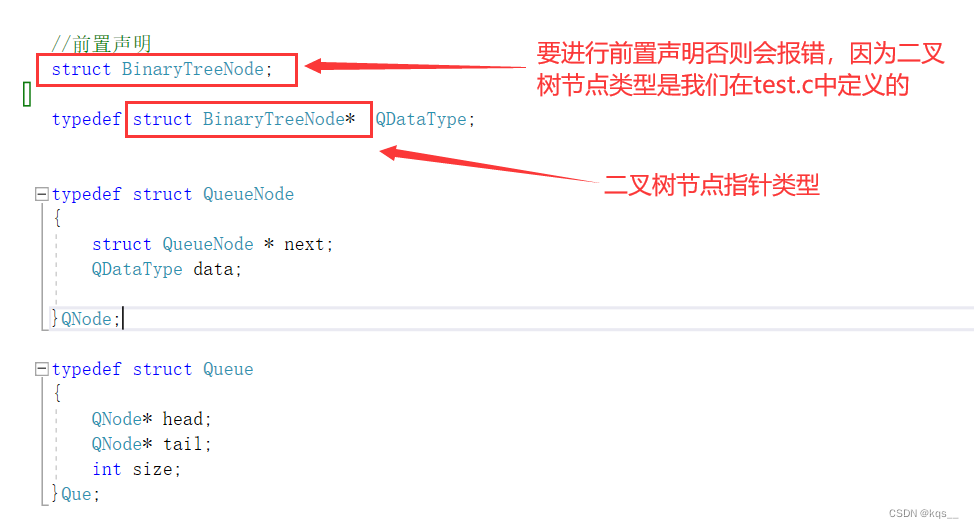
        我们在队列中存储的是节点的地址，所以我们要对队列结构体的数据域重定义，

        

 

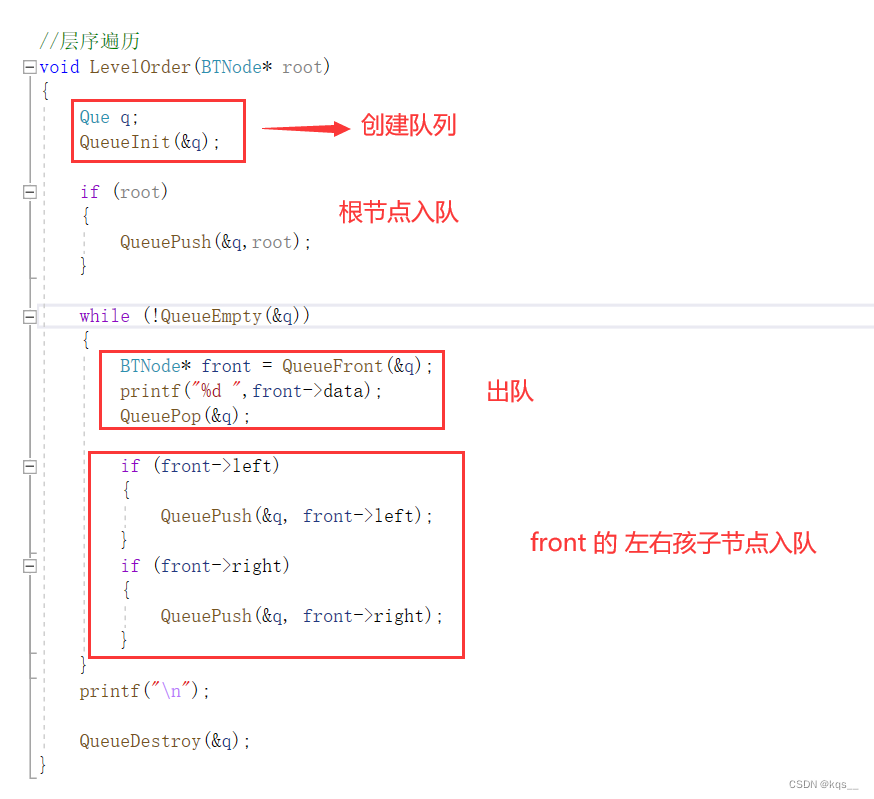
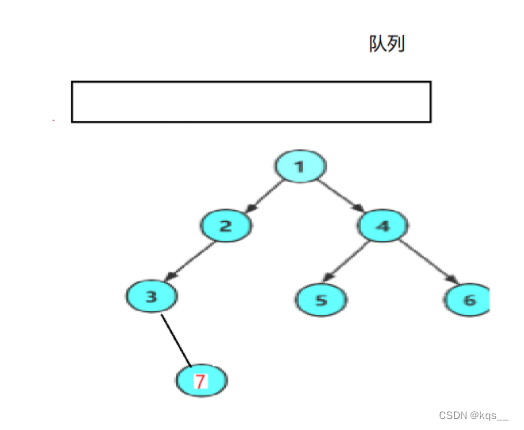
        以上代码 从逻辑上来讲就是1入队，1出队，2(1的左孩子)入队，4(1的右孩子)入队，2出队......

//层序遍历
void LevelOrder(BTNode* root)
{
	Que q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q,root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ",front->data);
		QueuePop(&q);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	printf("\n");

	QueueDestroy(&q);
}

2.完全二叉树的判断

        完全二叉树的判断和二叉树的层序的思想差不多，都需要借助队列来实现。

 

 

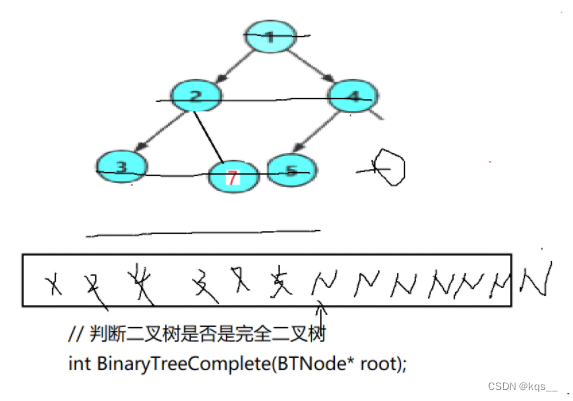
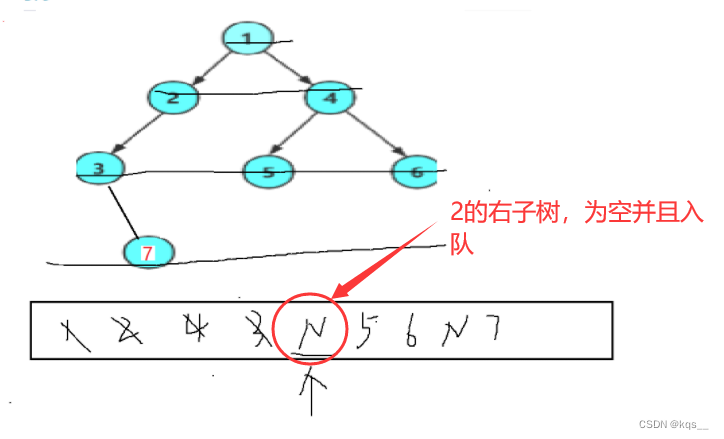
bool TreeComplete(BTNode* root)
{
	Que q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{

		BTNode* front = QueueFront(&q);
	//	printf("%d ", front->data);
		QueuePop(&q);

		if (front) //front的左子树 右子树 不管为不为空都入队
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break;//当front 为空的时候，跳出循环开始判断是否为完全二叉树
		}
	}

	while (!QueueEmpty(root))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front)
		{
			QueueDestroy(root);
			return false;
		}
	}
//	printf("\n");

	return true;
}