题目描述

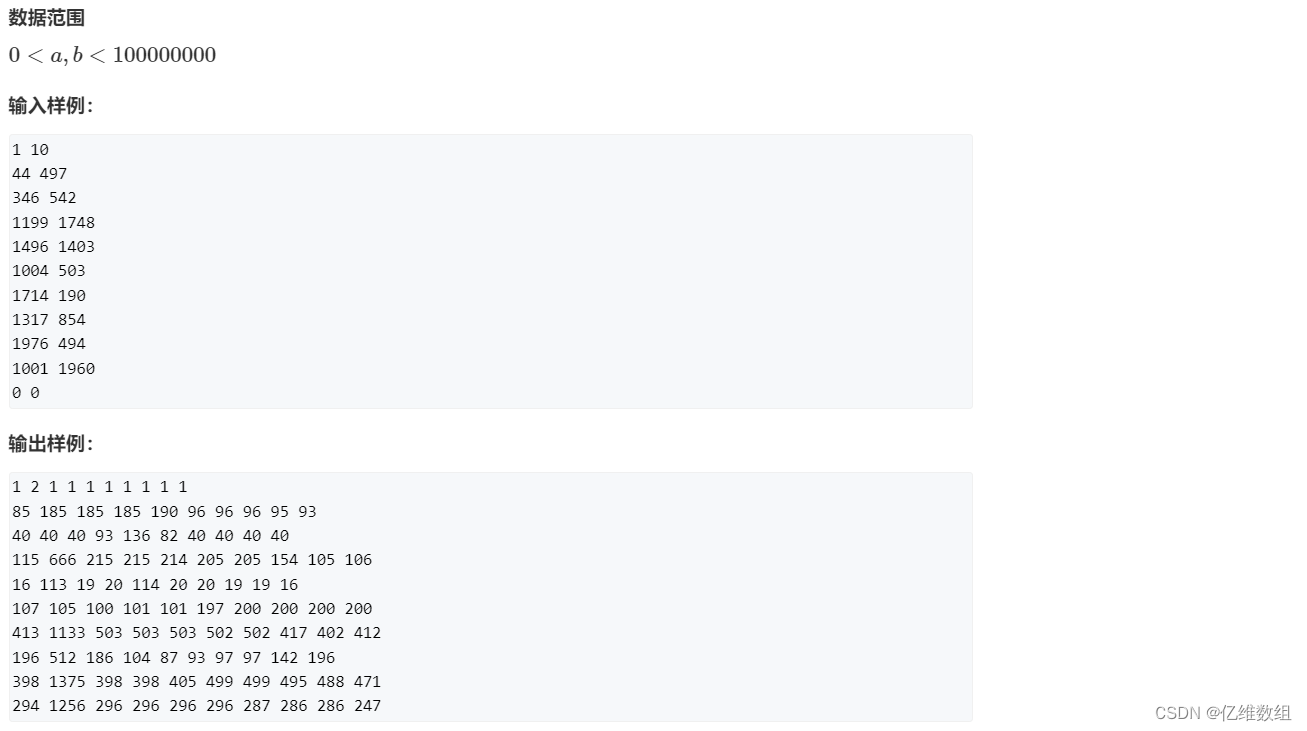举个栗子+分类讨论

求a~b中x的个数，可以转换为1~b中x的个数减去1~a-1中x的个数

所以核心是求1~n中x的个数，可以转换为求x在1~n中每一个数的每一位上出现的次数的和

假设要求1~abcdefg（这是一个七位数）中x=1的个数，可以求1在个位数上出现的总次数n1、1在十位数上出现的总次数n2、1在百位数上出现的总次数n3......以此类推，然后把n1、n2...求和，即为1~n之间所有数字1出现的总次数，同理其它数字0,2,3，...，9，也用类似的方式加起来即可。

现在以“1在第4位上出现的总次数”为例，进行分类讨论

1<=xxx1yyy<=abcdefg

如果xxx=0~abc-1，那么yyy可以取遍000~999，总共的情况数为：1000*abc

特例：如果在这里是求0在第4位上出现的总次数，那么xxx不能为0，此时总情况为999*abc

如果xxx=abc：

如果d<1，此时1不可能在第4位上出现

如果d=1，此时yyy可以取遍000~efg，总共efg+1种情况

如果d>1，此时yyy可以取遍000~999，总共1000种情况

所以当n=abcdefg时，“1在第4位上出现的总次数”就是1000*abc+efg+1+1000

当求1在其他位上出现的总次数时，只需要和上述类比即可

同理，求其他数字出现的次数时，和重复上述方法即可（注意上述说的x=0的一个小特殊情况）

代码与注释

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int a,b;
int power10(int i)//计算10的i次方
{
    int res=1;
    while(i)
    {
        res*=10;
        i--;
    }
    return res;
}
LL count(int n,int x)//统计1~n中x出现了多少次
{
    if(!n)return 0;
    LL res=0;
    int cnt=0;
    int temp=n;
    while(temp)
    {
        temp/=10;
        cnt++;
    }
    for(int i=0;i<cnt;i++)
    {
        int l=n/power10(i+1);//得到所求那一位的左边的数，比如例子中abcdefg,左边的就是abc，右边的就是efg
        int r=power10(i);//得到10的所求那一位的右边的位数次幂，比如例子中abcdefg，d右边的efg是三位数，得到1000
        if(x)res+=r*l;
        else res+=(l-1)*r;
        int d=(n/r)%10;//abcdefg中的d
        if(d==x)res+=(n%r)+1;
        else if(d>x)res+=r;
    }
    return res;
}
int main()
{
    while(cin>>a>>b,a||b)
    {
        if(a>b)swap(a,b);
        for(int i=0;i<=9;i++)
        cout<<count(b,i)-count(a-1,i)<<" ";
        cout<<endl;
    }
    return 0;
}