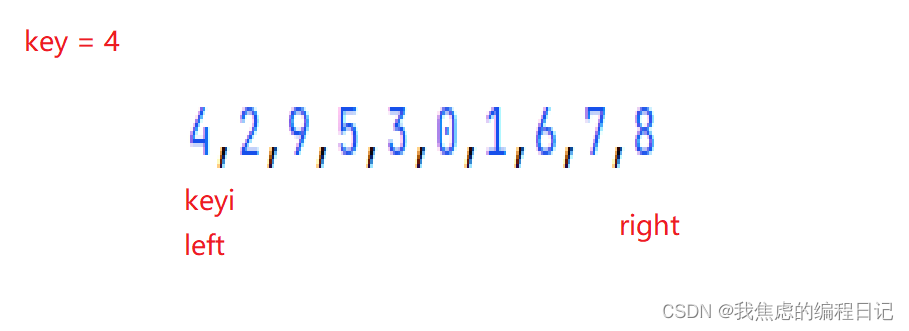定义

快排是Hoare在1962年（~~彼时的中国，是三年困难时期~~，好好学习建设祖国！）提出的基于二叉树结构的排序。

为什么说是基于二叉树？
因为这种排序每次选出一个基准值，然后将比其小的全部放在左边，大的放在右边。

这样就完成了一次循环。
接着这样就将这个数组分成了两半，一半大的，一半小的，

再对于这两半数组（相当于根节点（keyi的值）的两个子树）重复上述循环，直至只剩下一个元素或者没有的情况停止递归。

图解

定义三个下标

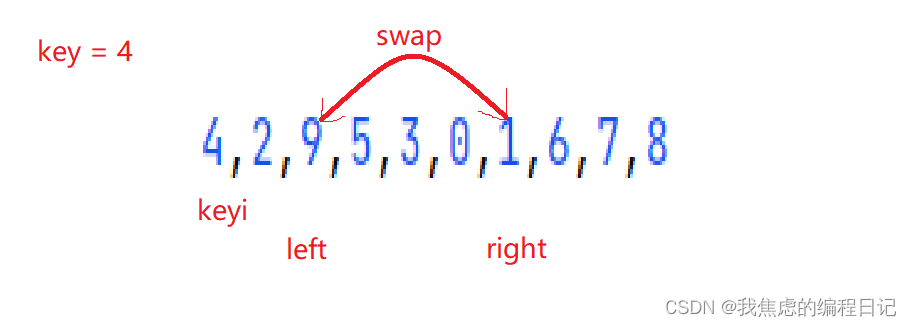
进行找大于key和小于key的值

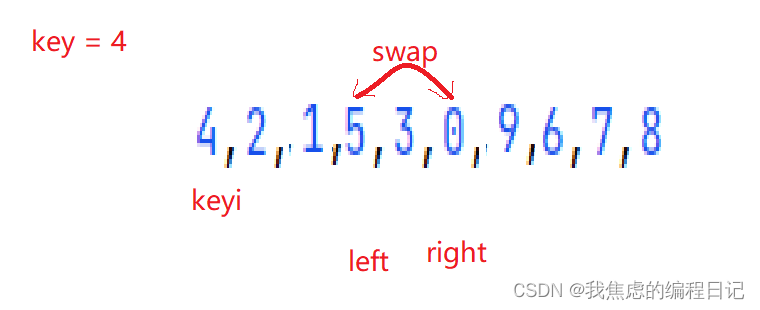
直到 left 和 right 相遇，进行交换 left 和 keyi 的值

一轮结束

4左边的都是小于4的，右边的都是大于4的。
左边的就是根节点4 的左子树，右边的就是根节点4 的右子树

重复上述过程，直至剩下一个或0个元素。

时间复杂度

最好情况：每次都能均分这个数组，最后是一个满二叉树或者完全二叉树，时间复杂度就是建树的时间，O(n * log₂n)。
最坏情况：有序的数组，每次都不能进行均分，是一棵单分支树，从前往后扫描每次都需要进行全部扫描，是一个等差数列，O(n²)。

空间复杂度

最好情况：递归建栈是一棵满（完全）二叉树的高度，为O(log₂n)。
最坏情况：是一棵单分支树，为O(n)。

稳定性

不稳定，交换会导致易位。

代码

/**
     * 快排Hoare法
     * @param array
     */
    public void quickSort(int[] array) {
        quickSort(array, 0, array.length-1);
    }

    /**
     * 进行递归选值放在key的左右
     * @param array
     * @param left
     * @param right
     */
    private void quickSort(int[] array, int left, int right) {
        // 直至剩下一个元素，那就为有序
        if (left >= right) return;
        // 至此，keyi的左边都是比他小的，右边都是比他大的
        int pivot = parttion(array, left, right);
        quickSort(array, left, pivot-1);
        quickSort(array, pivot+1, right);
    }
    private int parttion(int[] array, int left, int right) {

        int keyi = left;

        // 只要left在 right 的左边就说明没有遍历完
        while (left < right) {
            // 再加一条这样的规定，不然可能会right到-1处
            while (left < right && array[right] >= array[keyi]) {
                right--;
            }
            // 选大的放在右边
            while (left < right && array[left] <= array[keyi]) {
                left++;
            }

            // left 和 right 都找到了大于和小于下标在 keyi 的值
            // 如果这一轮没有找到大于和小于的，那就不交换了
            if (left == right) {
                break;
            }
            // 进行交换
            swap(array, left, right);
        }
        // 交换keyi的和相遇的
        swap(array, keyi, left);
        return left;
    }