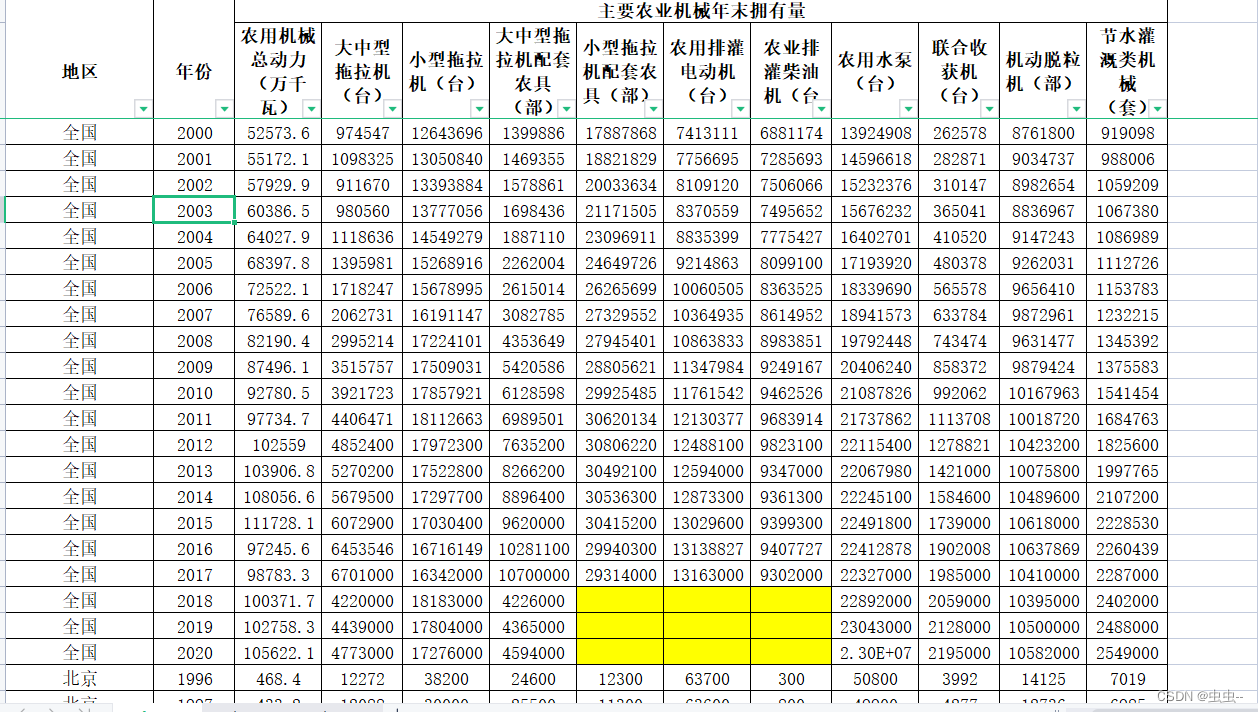
Problem - A - Codeforces
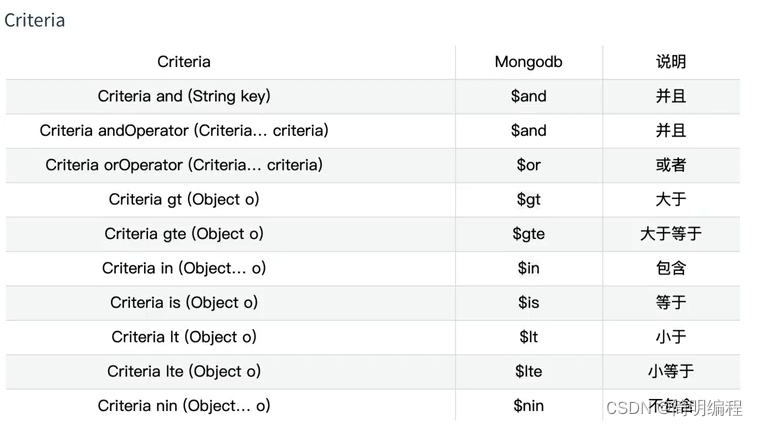
彭教授建造了n个不同高度的积木塔。第i座塔的高度为ai。
寿教授不喜欢这些塔,因为它们的高度是任意的。他决定首先精确地移除其中的m个,然后执行以下一些(或不执行)操作。
选择一座塔,将其高度ai增加1。
选择一座塔,把它的高度ai减少1。
选择一座塔,将其高度ai除以2,如果新的高度不是整数,则向下取整。
寿教授永远不能选择一个被移除的塔。如果在一次操作之后,塔的高度会变成0,那么这个操作是不允许的。在这些约束条件下,寿教授可以按照任意的顺序进行任意数量的操作。
寿教授希望所有未被移除的塔都有相同的高度。请计算出实现这一目标的最少操作数。
输入
第一行包含一个整数T(1≤T≤10),即测试案例的数量。
对于每个测试案例,第一行包含两个整数n,m (1≤n≤500,0≤m<n),即塔的数量,和塔的数量Prof.Shou在执行操作前应删除。
下一行包含n个整数a1,...,an(1≤ai≤109),即塔的初始高度。
输出
对于每个测试案例,在一行中输出最小的操作数。
例子
输入复制
3
2 0
2 6
5 0
1 2 3 4 5
5 3
1 2 3 4 5
输出拷贝
2
4
1
题解:
通过其给出的数据范围很小,我们应该推测出这并不是一个需要通过什么算法进行优化的题
我们直接暴力枚举所有可能的值
但是1e9数据范围也很大,那我们应该咋办呢?
其实可能值只会是每个塔的
for(int i = 1;i <= n;i++)
{
cin >> a[i];
int t = a[i];
while(t)
{
p[++idx] = t;
t = t/2;
}
}为什么是这样呢?
我们设最优解为t 与 t/2的两端中间的数
如果最优解在这部分因为我们已经把t/2存进去,所以答案要么是?-t/2,要么是t - ?
如果最优解比这个还要小
说明在t/2/2 ~ t/2之间,依次类推(结合完整代码后面看一下确实不太好理解)
#include<iostream>
#include<algorithm>
#include<string>
#include<queue>
#include<vector>
#include<map>
#include<cstring>
#include<cmath>
using namespace std;
#define int long long
int a[505];
int p[100005];
int cnt[100060];
void solve()
{
int n,m;
cin >> n >> m;
int idx = 0;
for(int i = 1;i <= n;i++)
{
cin >> a[i];
int t = a[i];
while(t)
{
p[++idx] = t;
t = t/2;
}
}
int ans = 1e18;
for(int i = 1;i <= n;i++)
{
int sum = 0;
for(int j = 1;j <= n;j++)
{
cnt[j] = 1e18;
if(p[i] > a[j])
{
cnt[j] = p[i] - a[j];
}
else if(p[i] == a[j])
{
cnt[j] = 0;
}
else
{
int k = a[j];
int s = 0;
while(k >= p[i])
{
if(k/2 <= p[i])
{
cnt[j] = min(k - p[i]+s,s + 1 + p[i] - k/2);
break;
}
s++;
k /= 2;
}
}
}
sort(cnt+1,cnt+n+1);
for(int i = 1;i <= n - m;i++)
{
sum += cnt[i];
}
ans = min(ans,sum);
}
cout << ans<<"\n";
}
//32 2 4
//32 16 8 4 2 1
//2 1
//4 2 1
signed main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);
// cout.tie(0);
int t = 1;
cin >> t;
while(t--)
{
solve();
}
}
//0 0 0 1 0 0 0 2