视频:GAN论文逐段精读【论文精读】_哔哩哔哩_bilibili
课程:CS231n 2022PPT笔记- 生成模型Generative Modeling
李宏毅机器学习——对抗生成网络(GAN)_iwill323的博客-CSDN博客
拓展网站:This Person Does Not Exist
https://www.reddit.com/r/MachineLearning/top/?t=month
https://crypko.ai/
博文:本文主要参考下面博文并摘取了文字和图片李沐论文精读系列一: ResNet、Transformer、GAN、BERT_神洛华的博客-
要想较为详细了解GAN,推荐博文:生成对抗网络,从DCGAN到StyleGAN、pixel2pixel,人脸生成和图像翻译。_神洛华的博客-CSDN博客_人像油画生成 对抗网络
目录
1.简介
2 导论
3 相关工作
4 目标函数及其求解
目标函数
1.生成器G
2.判别器D
3.两个模型同时训练
模型训练过程演示
迭代求解过程
5 理论结果:全局最优解 pg=pdata
收敛证明
6 GAN的优势与缺陷
优势
问题
7代码实现
8 影响
9. 关于损失函数的讨论
二元分类
discriminator
generator
1.简介
GANs(Generative Adversarial Networks,生成对抗网络)是从对抗训练中估计一个生成模型,其由两个基础神经网络组成,即生成器神经网络G(Generator Neural Network) 和判别器神经网络D(Discriminator Neural Network)
生成器G从给定噪声中(一般是指均匀分布或者正态分布)采样来合成数据,判别器D用于判别样本是真实样本还是G生成的样本。G的目标就是尽量生成真实的图片去欺骗判别网络D,使D犯错;而D的目标就是尽量把G生成的图片和真实的图片分别开来。二者互相博弈,共同进化,最理想的状态下,G可以生成足以“以假乱真”的图片G(z);对于D来说,它难以判定G生成的图片究竟是不是真实的,因此D(G(z)) = 0.5,此时噪声分布接近真实数据分布。

发展:
2 导论
深度学习是用来发现一些丰富的、有层次的模型,这些模型能够对AI里的各种数据做一个概率分布的表示。深度学习网络只是一种手段而已。
深度学习不仅是学习网络,更是对数据分布的一种表示。这和统计学习方法里面的观点不谋而合,后者认为机器学习模型从概率论的角度讲,就是一个概率分布Pθ(X) (这里以概率密度函数来代表概率分布)
机器学习的任务就是求最优参数θt ,使得概率分布 Pθ(X) 最大(即已发生的事实,其对应的概率理应最大)。
argmax 函数代表的是取参数使得数据的概率密度最大。求解最优参数θt的过程,我们称之为模型的训练过程( Training )
深度学习在判别模型上取得了很好的效果,但是在生成模型上比较差。难点在于最大化似然函数时,要对概率分布做很多近似,近似带来了很大的计算困难。
本文的核心观点就是, 不用再去近似似然函数了,可以用更好的办法(GAN)来计算模型。
GAN是一个框架,里面的模型都是MLP。生成器G这个MLP的输入是随机噪声,通常是高斯分布,然后将其映射到任何一个我们想去拟合的分布;判别器D也是MLP,所以可以通过误差的反向传递来训练,而不需要像使用马尔可夫链这样的算法对一个分布进行复杂的采样。这样模型就比较简单,计算上有优势。
3 相关工作
之前的生成模型总是想构造一个分布函数出来,同时这些函数提供了一些参数可以学习。这些参数通过最大化对数似然函数来求解。这样做的缺点是,采样一个分布时,求解参数算起来很难,特别是高维数据。因为这样计算很困难,所以最近有一些Generative Machines,不再去构造分布函数,而是学习一个模型来近似这个分布。
前者真的是在数学上学习出一个分布,明明白白知道数据是什么分布 ,里面的均值方差等等到底是什么东西。而GAN就是通过一个模型来近似分布的结果,而不需要构造分布函数。这样计算起来简单,缺点是不知道最终的分布到底是什么样子。
对f的期望求导,等价于对f自己求导。这也是为什么通过误差反向传递来对GAN求解。
- 光看上面描述看不懂,可以简单参考:CS231n 2022PPT笔记- 生成模型Generative Modeling_iwill323的博客-CSDN博客_cs231n2022
生成模型可以解决密度估计问题,有两种方式:
- 显式密度模型会显式地给出一个和输入数据的分布pmodel(x)
- 隐式密度模型训练一个模型,从输入数据中采样,并直接输出样本,而不用显式地给出分布的表达式。

4 目标函数及其求解
目标函数
GAN最简单的框架就是模型都是MLP。
1.生成器G
生成器是要在数据x上学习一个分布pg(x),其输入是定义在一个先验噪声z上面,z的分布为pz(z),比如高斯分布。生成模型G的任务就是用MLP把噪声z映射成数据x。比如图片生成,假设不同的生成图片是100个变量控制的,而MLP理论上可以拟合任何一个函数,那么我们就构造一个100维的向量,MLP强行把z映射成x,从而生成像样的图片。z可以先验的设定为一个100维向量,其均值为0,方差为1,呈高斯分布。这么做优点是算起来简单,缺点是MLP并不是真的了解背后的z是如何控制输出的,只是学出来随机选一个比较好的z来近似x,所以最终效果也就一般。
2.判别器D
判别器输出一个标量(概率),判断其输入是G生成的数据,还是真实的数据。对于D,真实数据label=1,假的数据label=0
3.两个模型同时训练
最终目标函数公式如下所示,E代表期望,公式中同时有minmax,所以是对抗训练。
![]()
G表示生成网络,D 表示判别网络,θd是判别器参数,θg是生成器的参数,训练目标是让目标函数在θg上取得最小值,同时在 θd上取得最大值。
- 第一项:pdata 表示真实数据的分布。D(x)是判别器网络对真实数据(训练数据)x的判别结果,输出一个 0-1 的概率(0表示假,1表示真)。E表示我们考虑的是整个训练集中所有样本的一个期望,而不是具体某个样本的概率。
- 第二项:p(z)表示噪声的分布。使用 G(z) 可以生成一个样本,D(G(z))代表了判别器网路对生成的伪数据的判别结果。
- θd的目标:整个表达式越大越好。希望logD(x) 越大越好,即判别器对于真实样本的判别为真的期望越大越好;希望 log(1−D(G(z)))越大越好,也就是希望判别器对假的样本判别为真的概率越小越好。因此如果能最大化这一结果,就意味着判别器能够很好的区别真实数据和伪造数据。
- θg的目标:整个式子越小越好。G的目标是希望生成的图片越接近真实越好,使得D(G(z))接近1,也就是最小化log(1−D(G(z)))。结果就是训练一个G,使判别器尽量犯错,无法区分出数据来源,意味着生成器在生成与真实样本非常相似的数据
3模型训练过程演示
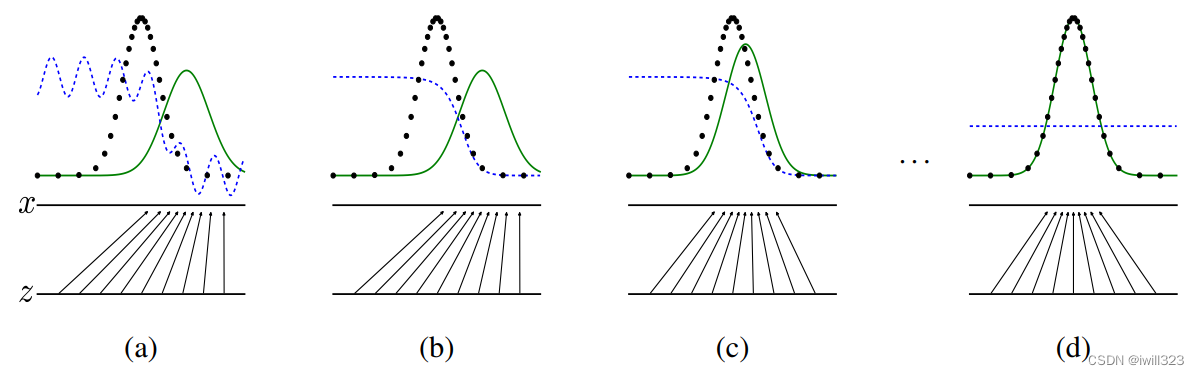
如上图所示,假设x和z都是一维向量,且z是均匀分布。虚线点为真实数据分布,蓝色虚线是判别器D判别结果的分布,绿色实线为生成器G的分布。
a. 生成器从均匀分布学成绿色实线表示的高斯分布,这时候判别器还很差;
b. 判别器学成图b所示的分布,可以把真实数据和生成数据区别开来;
c. 随着训练进行,生成器波峰靠向真实数据波峰,使得判别器难以分辨了;辨别器为了更准,其分布也往真实数据靠拢;
d. 最终训练的结果,生成器拟合真实分布,判别器难以分辨,输出概率都为0.5,即D(x) = 1/2
迭代求解过程
下面是具体的算法过程:

完整的训练过程:在每一个训练迭代期都先训练判别器网络,然后训练生成器网络。
- 1)对于判别器网络,先从噪声先验分布z中采样得到一个小批量样本,接着从训练数据x中采样获得小批量的真实样本,将噪声样本传给生成器网络,并在生成器的输出端获得生成的图像。此时我们有了一个小批量伪造图像和小批量真实图像,在判别器生进行一次梯度计算,利用梯度信息更新判别器参数,按照以上步骤迭代k次来训练判别器。
- 2)训练生成器,采样获得一个小批量噪声样本,将它传入生成器,对生成器进行反向传播,优化目标函数。
训练完之后,将噪声图像传给生成网络,就能生成伪造图像。
Optimizing D to completion in the inner loop of training is computationally prohibitive, and on finite datasets would result in overfitting. Instead, we alternate between k steps of optimizing D and one step of optimizing G. This results in D being maintained near its optimal solution, so long as G changes slowly enough.
k是一个超参数,不能太小也不能太大。要保证判别器D可以足够更新,但也不能更新太好。
- 如果D更新的不够好,那么G训练时在一个判别很差的模型里面更新参数,继续糊弄D意义不大;
- 如果D训练的很完美,那么 log(1−D(G(z)))趋近于0,求导结果也趋近于0,生成器难以训练
- 整体来说GAN的收敛是很不稳定的,所以之后有很多工作对其进行改进。
另一个问题:
早期G非常弱,所以很容易把D训练的很好,这样就造成刚刚说的G训练不动了。
In practice, equation 1 may not provide sufficient gradient for G to learn well. Early in learning, when G is poor, D can reject samples with high confidence because they are clearly different from the training data. In this case, log(1 - D(G(z))) saturates.
所以作者建议G的目标函数改为最大化logD(G(z)),这样可以得到同样的G和D的不动点,同时又能在早期更好的下降。
Rather than training G to minimize log(1 - D(G(z))) we can train G to maximize log D(G(z)). This objective function results in the same fixed point of the dynamics of G and D but provides much stronger gradients early in learning
下面从优化目标曲线的形状角度来解释:

上图的蓝色曲线为 log(1−D(G(z)))。当生成器效果不好(D(G(z)接近0)时,梯度非常平缓,模型训练很慢;当生成器效果好(D(G(z)接近1)时,梯度很陡峭,模型更新地会过快。这就与我们期望的相反了,我们希望在生成器效果不好的时候梯度更陡峭,这样能学到更多,在即将收敛的时候应该放缓更新步伐。
max logD(G(z))图像如下图绿色曲线所示,它就有很好的特性,即初始时梯度大,最后梯度小,符合训练的需要,实际训练中基本都用这个式子。

李沐:带来的问题是,D(G(z))→0的时候,log0是负无穷大,会带来数值上的问题。
关于目标函数的部分让人看的云里雾里,其实说白了就是二分类问题误差函数的构造,比如,我们会去min -log(y^),会去min -log(1-y^),而不会去min log(1-y^),见最后一部分的讨论
5 理论结果:全局最优解 pg=pdata
具体证明部分可以参考帖子GAN论文阅读——原始GAN(基本概念及理论推导)_StarCoo的博客-CSDN博客_gan 原始论文
1.先训练D。固定生成器G,最优的辨别器应该是

- *表示最优解
- pg(x) 和 pdata(x)分别表示x在生成器拟合的分布里和真实数据的分布里,它的概率分别是多少。
- 当pg(x)=pdata(x)时,结果为1/2,表示两个分布完全相同,最优的判别器也无法将其分辨出来。
- 这个公式的意义是,从两个分布里面分别采样数据,用目标函数 min max V(D,G)训练一个二分类器,如果分类器输出的值都是0.5,则可以认为这两个分布是完全重合的。在统计学上,这个叫two sample test,用于判断两块数据是否来自同一分布。
注:two sample test是一个很实用的技术,比如在一个训练集上训练了一个模型,然后部署到另一个环境,需要看看测试数据的分布和训练数据是不是一样的,就可以像这样训练一个二分类器,看能否区分数据来源,避免部署的环境和我们训练的模型不匹配。
证明:
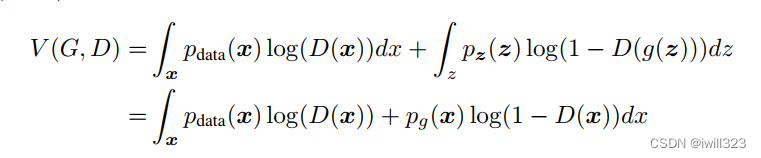
第一行是密度函数求积分,换元g(z)=x得到第二行(这个换元没看懂)
假设上面看懂了,那么后面的就简单了。在数据给定,G 给定的前提下, Pdata(x)与 PG(x)都可以看作是常数,我们可以分别用 a,b来表示他们,这样我们就可以得到如下的式子:

证毕。
2.然后训练G。把D的最优解代回目标函数,目标函数只和G相关,写作C(G):
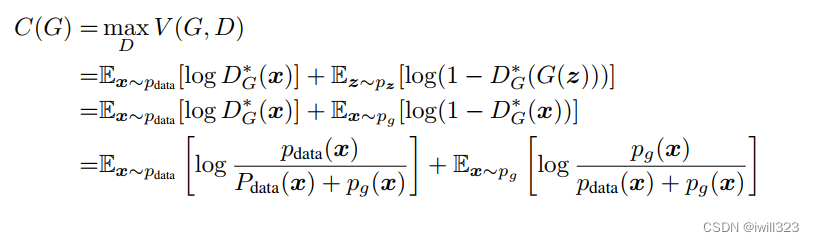
现在只需要最小化这一项就行。
可以证明,当且仅当pg=pdata时有最优解 C(G)=−log4。
- 上式两项可以写成KL散度,KL散度用来衡量这两个分布的差异,
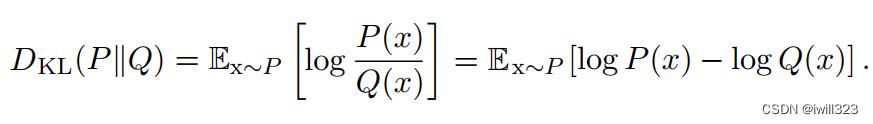
它表示了假如我们采取某种编码方式使编码Q分布所需的比特数最少,那么编码P分布所需的额外的比特数。假如P和Q分布完全相同,则其KL divergence 为零。
KL散度有很多有用的性质,最重要的是,它是非负的。KL散度为0,当且仅当P和Q在离散型变量的情况下是相同的分布,或者在连续型变量的情况下是“几乎处处”相同的。
使用KL散度,简化上面的式子:

- 又因为JS散度定义为:

所以进一步化简成:

要求 minC(G),当且仅当最后一项等于0的时候成立(JS散度≥0),此时pg=pdata,表示两个分布完全相同,带入到D*(x)表达式,结果为1/2,最优的判别器也无法将其分辨出来。
注:JS散度跟KL散度的区别是前者是对称的,pg和 pdata可以互换,而后者不对称。
综上所述,目标函数 min maxV(D,G)有全局最优解,这个解当且仅当 pg=pdata时成立,也就是生成器学到的分布等于真实数据的分布,可以取得最优生成器。
The global minimum of the virtual training criterion C(G) is achieved if and only if pg = pdata. At that point, C(G) achieves the value - log 4.
收敛证明
这部分证明了:给定足够的训练数据和正确的环境,在算法1中每一步允许D达到最优解的时候,对G进行下面的迭代:

训练过程将收敛到pg=pdata,此时生成器G是最优生成器。
其实我们每次只是k个steps训练D,离上述前提条件还很远,结论是否真的适用,就不那么好说了
6 GAN的优势与缺陷
参考GAN论文阅读——原始GAN(基本概念及理论推导)_StarCoo的博客-CSDN博客_gan 原始论文
优势
与其他生成式模型相比较,生成式对抗网络有以下四个优势深度 | OpenAI Ian Goodfellow的Quora问答:
- 比其它模型生成效果更好(图像更锐利、清晰)。
- GAN能训练任何一种生成器网络(理论上-实践中,用 REINFORCE 来训练带有离散输出的生成网络非常困难)。大部分其他的框架需要该生成器网络有一些特定的函数形式,比如输出层是高斯的。重要的是所有其他的框架需要生成器网络遍布非零质量(non-zero mass)。
- 不需要设计遵循任何种类的因式分解的模型,任何生成器网络和任何判别器都会有用。
- 无需利用马尔科夫链反复采样,无需在学习过程中进行推断(Inference),回避了近似计算棘手的概率的难题。
问题
GAN目前存在的主要问题:
- 难以收敛(non-convergence)
目前面临的基本问题是:所有的理论都认为 GAN 应该在纳什均衡(Nash equilibrium)上有卓越的表现,但梯度下降只有在凸函数的情况下才能保证实现纳什均衡。当博弈双方都由神经网络表示时,在没有实际达到均衡的情况下,让它们永远保持对自己策略的调整是可能的深度深度 | OpenAI Ian Goodfellow的Quora问答
- 难以训练:崩溃问题(collapse problem)
GAN模型被定义为极小极大问题,没有损失函数,在训练过程中很难区分是否正在取得进展。GAN的学习过程可能发生崩溃问题,生成器开始退化,总是生成同样的样本点,无法继续学习。当生成模型崩溃时,判别模型也会对相似的样本点指向相似的方向,训练无法继续。
- 无需预先建模,模型过于自由不可控。
与其他生成式模型相比,GAN不需要构造分布函数,而是使用一种分布直接进行采样,从而真正达到理论上可以完全逼近真实数据,这也是GAN最大的优势。然而,这种不需要预先建模的方法缺点是太过自由了,对于较大的图片,较多的 pixel的情形,基于简单 GAN 的方式就不太可控了(超高维)。
所以可以看到,最终作者生成的图片分辨率都很低。在GAN 中,每次学习参数的更新过程,被设为D更新k回,G才更新1回,也是出于类似的考虑。
7代码实现
代码:李宏毅机器学习作业6-使用GAN生成动漫人物脸
CS231n对抗生成网络代码
pytorch版参考 https://pytorch.org/tutorials/beginner/dcgan_faces_tutorial.html
8 影响
1.开创了GAN这个领域
2.GAN本身是无监督学习,不需要标注数据。GAN的思想应用于无监督学习。
3.其训练方式是用有监督学习的损失函数来做无监督学习(有监督的标签来源于数据是真实的还是生成的),所以训练上会高效很多。这也是之后bert之类自监督学习模型的灵感来源。再如Domain Adversarial Training李宏毅机器学习作业11——Transfer Learning,Domain Adversarial Training
9. 关于损失函数的讨论
下面是个人一些思考,简单来说,就是论文中对GAN的优化目标函数的设计看似复杂,其实就是一个二元分类损失函数
二元分类
GAN的训练过程是一个minmax训练,但是几乎没有人会真的使用梯度上升的方法,所以实作和理论有出入。下面先看二元分类问题的损失函数,希望该Loss function越小越好。y^是模型预测结果,y是标签
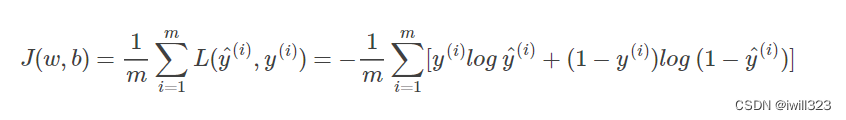
当y=1时,L(y^,y)=−log y^。如果y^越接近1,L(y^,y)≈0,表示预测效果越好;如果y^越接近0,L(y^,y)≈+∞,表示预测效果越差。
当y=0时,L(y^,y)=−log (1−y^)。如果y^越接近0,L(y^,y)≈0,表示预测效果越好;如果y^越接近1,L(y^,y)≈+∞,表示预测效果越差。
discriminator
下面是discriminator损失函数
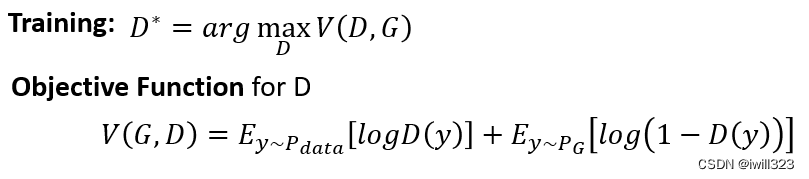
套用二元分类的损失函数,让y^=D(y)。当数据采集自Pdata时,标签y=1,损失函数为−log y^;当数据采集自PG时,标签y=0,损失函数为−log (1−y^)。将二者相加,其实就是V(G,D)的相反数,也就是说,训练discriminator可以直接使用二元交叉熵损失(BCELoss),其中真实图片的label为1,生成的图片的label为0
r_label = torch.ones((bs)).to(self.device)
f_label = torch.zeros((bs)).to(self.device)
r_loss = self.loss(r_logit, r_label)
f_loss = self.loss(f_logit, f_label)
loss_D = (r_loss + f_loss) / 2generator
下面是generator损失函数
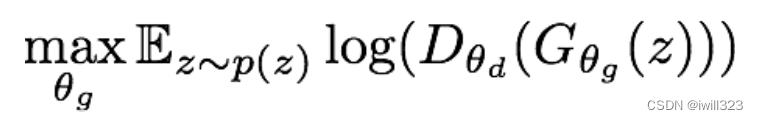
套用二元分类的损失函数,让y^=D(G(z)),让标签y=1,则损失函数为−log y^,所以也可以直接使用二元交叉熵损失(BCELoss),只要指定label为1
loss_G = self.loss(f_logit, r_label)![]()

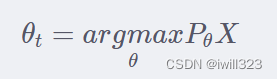


![[Java]图论进阶--最小生成树算法](https://img-blog.csdnimg.cn/eafbaf0027424319ac519b13f98f3639.png)