基本算法学习记录---Day2

news2024/11/28 8:47:18

并查集模板1

class Solution {
    int[] root = new int[200000];
    public int Que() {
    	//初始化
        for(int i = 1;i<=n;i++){
            root[i] = i;
        }
        //TODO
    }
    //找根(将节点连接)
    public int find(int x){
        if(root[x] != x){
            root[x] = find(root[x]);
        }
        return root[x];
    }
    //合并
    public void heb(int i,int j){
        root[find(i)] = find(j);
    }
}

并查集模板2（按秩合并）

前置知识：**按秩合并——主要是针对heb函数**，在合并两个集合时，将秩大的根节点设置为秩小的根节点的父节点。意思是当要合并两个根节点A、B时，如果节点A的秩大于节点B的秩，那么将节点A设置为节点B的父节点，反之亦然。
按秩合并可以最小化树的深度。

class Solution {
    int[] root = new int[100001];//根
    int[] rank = new int[100001];//秩
    //TODO
    /*其他参数(可记录：
    				1.合并完后的总连通分量数n-minusCount)
    				2.制造出环的边的数量superfluousCount
    				3.每个连通分量中的节点数量size
    				4.每个连通分量中的边权值和weight
    */  
    public int Que(int n//n个节点) {
    	//初始化
        for(int i = 0;i<n;i++){//
            root[i] = i;
        }
        //TODO
    }
    //找根(将节点连接)
    public int find(int x){
        if(root[x] != x){
            root[x] = find(root[x]);
        }
        return root[x];
    }
    //合并
    public void heb(int i,int j){
        int rootA = find(i);
        int rootB = find(j);
        if(rootA != rootB){
        	//按秩合并
            if(rank[rootA] < rank[rootB]){
                int temp = rootA;
                rootA = rootB;
                rootB = temp;
            }
            root[rootB] = rootA;
            if (rank[rootA] == rank[rootB]){
                rank[rootA] += 1;
            }
            //TODO
        }else{
            //TODO
        }
    }
}

tip：无向图考虑并查集，有向图考虑深度广度优先、拓扑排序。

leetcode上比较经典的题有：547. 省份数量、684. 冗余连接、1319. 连通网络的操作次数、1971. 寻找图中是否存在路径（未完待续…）

547. 省份数量——求连通分量的数量（可直接套模板1）

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市
c 间接相连。

省份是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中省份的数量。
示例 1：

输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

代码

class Solution {
    int[] root = new int[205];
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        for(int i = 1;i<=n;i++){
            root[i] = i;
        }
        for(int i = 0;i<n;i++){
            for(int j = 0;j<n;j++){
                if(isConnected[i][j] == 1 && i != j){
                    heb(i+1,j+1);
                }
            }
        }
        int ans = 0;
        for(int i = 1;i<=n;i++){
            if(root[i] == i){
                ans++;
            }
        }
        return ans;
    }
    public int find(int x){
        if(root[x] != x){
            root[x] = find(root[x]);
        }
        return root[x];
    }
    public void heb(int i,int j){
        root[find(i)] = find(j);
    }
}

1319. 连通网络的操作次数（需要对模板进行优化——按秩合并，套模板2）

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。
网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。
给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。
示例 1：

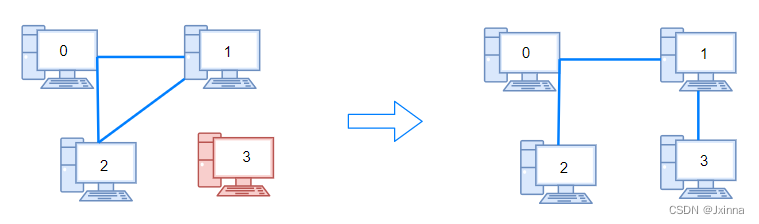
输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

前置知识：
1.存在N个节点和M条边，被边直接或间接相连的所有节点共同形成一个域，称为连通域，连通域也称为连通分量。
2.若有K个连通分量，则最少需要K-1条边才能将K个连通分量合并成1个连通分量。

代码

class Solution {
    int[] root = new int[100001];//根
    int[] rank = new int[100001];//秩
    int superfluousCount = 0;//多余的边(制造出环的边)
    
    int minusCount = 0;//记录减去的连通分量的数目   
    public int makeConnected(int n, int[][] connections) {
        int len = connections.length;
        for(int i = 0;i<n;i++){
            root[i] = i;
        }
        for(int i = 0;i<len;i++){
            heb(connections[i][0],connections[i][1]);
        }
        //(n-minusCount即为剩余的连通分量的个数)
        if(superfluousCount < n-minusCount-1){//此时不能使所有计算机都连通
            return -1;
        }
        //n个连通分量连成一个需要n-1条边
        return n-minusCount-1;
    }
    public int find(int x){
        if(root[x] != x){
            root[x] = find(root[x]);
        }
        return root[x];
    }
    public void heb(int i,int j){
        int rootA = find(i);
        int rootB = find(j);
        if(rootA != rootB){//不是多余连接的情况(即没有环)
        	//按秩合并
            if(rank[rootA] < rank[rootB]){
                int temp = rootA;
                rootA = rootB;
                rootB = temp;
            }
            root[rootB] = rootA;
            if (rank[rootA] == rank[rootB]){
                rank[rootA] += 1;
            }
            //每合并一次则令减去的连通分量的数目+1
            minusCount++;
        }else{//是多余连接的情况(即形成环)
            //此时记录多余的边
            superfluousCount++;
        }
    }
}