开始系统学习算法啦!为后面力扣和蓝桥杯的刷题做准备!这个专栏将记录自己学习算法是的笔记,包括概念,算法运行过程,以及代码实现,希望能给大家带来帮助,感兴趣的小伙伴欢迎评论区留言或者私信博主哦!今天更新的是《03_2排序算法:快速排序、归并排序》
目录
快速排序概念
算法步骤
时间复杂度
算法实现
总结
归并排序概念
算法步骤
时间复杂度
程序实现
总结
快速排序概念
快速排序(Quicksort),又称为交换排序,通过一趟排序将要排序的数据分割为独立的两部分。假设要排序的列表是A[0]...A[N-1],首先任意选取一个数据(通常选用列表的第一个数)作为基准数据,一般我们都选择第一个数作为基准数据,然后将所有比它小的数都放到它的左边,所有比它大的数都放到它的右边,这个过程称为快速排序。值得注意的是,快速排序不是一种稳定的排序算法,也就是说,多个相同的值的相对位置也许会在算法结束时产生变化。
算法步骤
- 设置两个low、high,排序开始的时候:low=0,high=N-1
- 以第一个列表元素作为基准数据,赋值给mid,即mid=A[0]

- 从high开始向前搜索,即由后开始向前搜索(high--),找到第一个小于mid的值A[high],将A[high]和A[low]的值交换
- 从low开始向后搜索,即向前开始向后搜索(low++),找到大于mid的A[low],将A[low]和A[high]的值交换。
- 重复第3、4步,直到low=high;
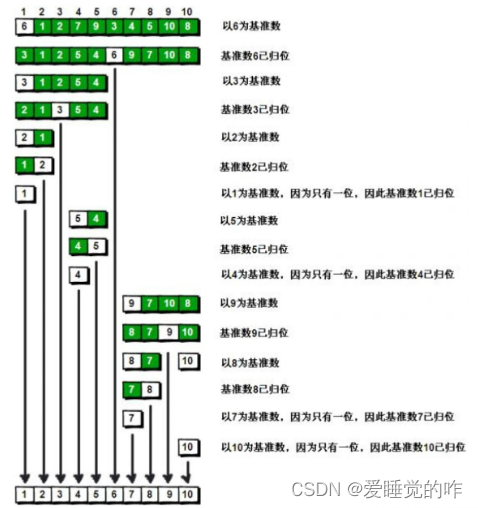
时间复杂度
- 最优时间复杂度:O(nlogn) #每次分成两半,要分logn次,再乘遍历的n次
- 最坏时间复杂度:O(n2) #每次只分出一个元素出来,要分n次,再乘遍历的n次
- 稳定性:不稳定
算法实现
def quick_sort(alist,start,end):
"""
:param alist:
:return:alist.sort
快速排序首先要选择一个基准,将其他数据与这个基准比较,比它大的放右边,比它小的放左边,循环这个过程,完成排序
定义两个指针,一个low一个high,
开始是high先做比较,如果high对应的元素比基准大就不懂,high--,如果比基准小,则与low对应的元素交换,然后low++
直到low==high说明一趟快速排序已经完成,再将基准添加到序列中
上面已经完成一次快速排序,再将左序列和右序列进行递归,注意设置一个出口,即可完成整个遍历
以alist = [5,1,3,2,8,7,6,4]为例
以alist = [4,1,3,2,8,7,6,4]为例
"""
# 递归的出口
if start >= end:
return
mid = alist[start] # 定义基准 5
low = start # 左指针
high = end # 右指针 7
# 判断high是不是大于mid,大于的话就不用交换,之间high--,直到小于的时候进行交换
while low <high:
while alist[high] >= mid and high > low: #7>0
high -=1
alist[low] = alist[high]
#判断low是不是小于mid, 小于的话就不用交换,之间low++,直到大于的时候进行交换
while alist[low] < mid and high>low:
low += 1
alist[high] = alist[low]
alist[low] = mid
quick_sort(alist,0,low-1)
quick_sort(alist,low+1,end)
return alist总结
主要是两个指针的交替变化,可以用while循环来执行,判断high是不是大于mid,大于的话就不用交换,之间high--,直到小于的时候进行交换;判断low是不是小于mid, 小于的话就不用交换,之间low++,直到大于的时候进行交换;最后再加上基准,这样就完成一次快速排序,之后再从外面用一个while循环,里面用递归思想不断对左序列和右序列进行操作,记得写一个出口,start >= end,这样快速排序算法就结束了。
归并排序概念
归并排序(Merge sort)是采用分治法的一个非常典型的应用。归并排序的思想就是先递归分解数组,再合并数组。将数组分解最小之后,然后合并两个有序数组,基本思想是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就向后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
算法步骤
先分再合:

时间复杂度
- 最优时间复杂度:O(nlogn)
- 最坏时间复杂度:O(nlogn)
- 稳定性:稳定
程序实现
def Merge_sort(alist):
"""
主要思想就是分治法,先拆分再合并
整个框架是递归算法,既包括拆解成一个一个的列表,也包列表的缝合
以为[5,1,3,2,8,7,6,4]例,拆解成[5],[1],[3],[2],[8],[7],[6],[4]
第一次合并成[1,5],[2,3],[7,8],[4,6]
第二次合并成[1,2,3,5],[4,6,7,8]
第三次合并成[1,2,3,4,5,6,7,8]
:param alist:
:return: alist.sort
"""
n = len(alist)
mid = n //2
if n <= 1:
return alist
left_list = Merge_sort(alist[0:mid])
right_list = Merge_sort(alist[mid::])
left_p = 0 # 定义左指针
right_p = 0 # 定义右指针
result_list =[]
while left_p < len(left_list) and right_p < len(right_list):
if left_list[left_p] < right_list[right_p]:
result_list.append(left_list[left_p])
left_p += 1
else:
result_list.append(right_list[right_p])
right_p += 1
result_list.extend(left_list[left_p::])
result_list.extend(right_list[right_p::])
return result_list总结
主要思想就是分治法,先拆分再合并,整个框架是递归算法,既包括拆解成一个一个的列表,也包列表的缝合。定义两个指针,一个左指针,一个右指针,先比较两个指针指向的的元素大小,将小的元素添加到目标序列中,然后该指针+1继续比较,直到某一个指针走到头,此时将另一个指针指向元素的后面元素全部添加到目标序列中。