排序数组

难度：中等

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

堆排序

思路：
许多应用程序都需要处理有序的元素，但不一定要求他们全部有序，或者不一定要一次就将他们排序，很多时候，我们每次只需要操作数据中的最大元素(最小元素)，那么有一种基于二又堆的数据结构可以提供支持。

所谓二叉堆，是一个完全二叉树的结构，同时满足堆的性质：即子结点的键值或索引总是小于(或者大于)它的父节点。在一个二又堆中，根节点总是最大(或者最小)节点，这样堆我们称之为最大(小)堆。

堆排序算法就是抓住了这一特点，每次都取堆顶的元素，然后将剩余的元素重新调整为最大(最小)堆，依次类推，最终得到排序的序列。

堆排序初始时把要排序的数的序列看作是一棵顺序存储的二叉树，调整它们的存储序，使之成为一个堆，这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。

完全二叉树特性：

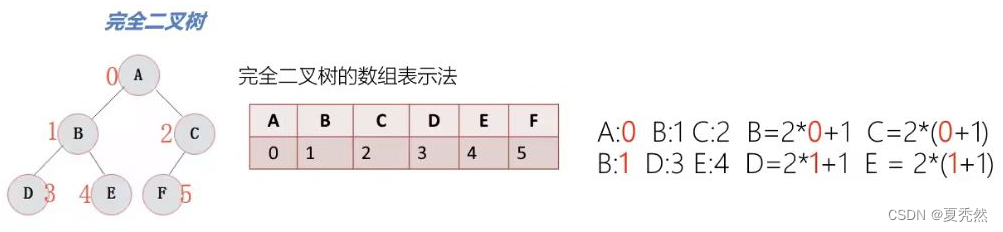
• 推论1： 对于位置为K的结点 左子结点=2k+1 右子结点=2(k+1)
  验证：C:2 22+1=52(2+1)=6
• 推论2： 最后一个非叶节点的位置为 (N/2)-1，N为数组长度
  验证：数组长度为6，(6/2)-1=2

时间复杂度： $O(nlogn)$，第一次构建最大堆的时候时间复杂度为 $O(n)$，后续弹出堆顶元素后重建堆过程的时间复杂度 $O(nlogn)$，最终时间复杂度为：$O(n)+O(nlogn)=O(nlogn)$。
空间复杂度： $O(1)$，原地排序算法。

class Solution:
    def adjustHeap(self, nums, index, length):
        l, r = 2*index+1, 2*(index+1)
        maxIndex = index
        if l < length and nums[l] > nums[maxIndex]:
            maxIndex = l
        if r < length and nums[r] > nums[maxIndex]:
            maxIndex = r
        if maxIndex != index:
            nums[index], nums[maxIndex] = nums[maxIndex], nums[index]
            self.adjustHeap(nums, maxIndex, length)

    def sortArray(self, nums: List[int]) -> List[int]:
        length = len(nums)
        # 构建一个最大堆
        for i in range(int(length/2-1), -1, -1):
            self.adjustHeap(nums, i, length)
        # 堆排序
        while length > 1:
            nums[0], nums[length-1] = nums[length-1], nums[0]
            length -= 1
            self.adjustHeap(nums, i, length)
        return nums

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/sort-an-array