1 题目描述

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。问总共有多少条不同的路径？

示例 1：
在这里插入图片描述
输入：m = 3, n = 7
输出：28

示例 2：
输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。

向右 -> 向下 -> 向下
向下 -> 向下 -> 向右
向下 -> 向右 -> 向下

示例 3：
输入：m = 7, n = 3
输出：28

示例 4：
输入：m = 3, n = 3
输出：6

2 算法设计

确定dp数组，（dp table）以及下标的含义
dp数组为一个二维数组，dp[i]表示走到第i个位置有多少种不同路径

        int[][] dp = new int[m][n];

dp数组初始化
因为只能向右或向下走，所以第0行的所以位置只有一种的路径，因此将dp的第一行初始化为1。
确定递推公式

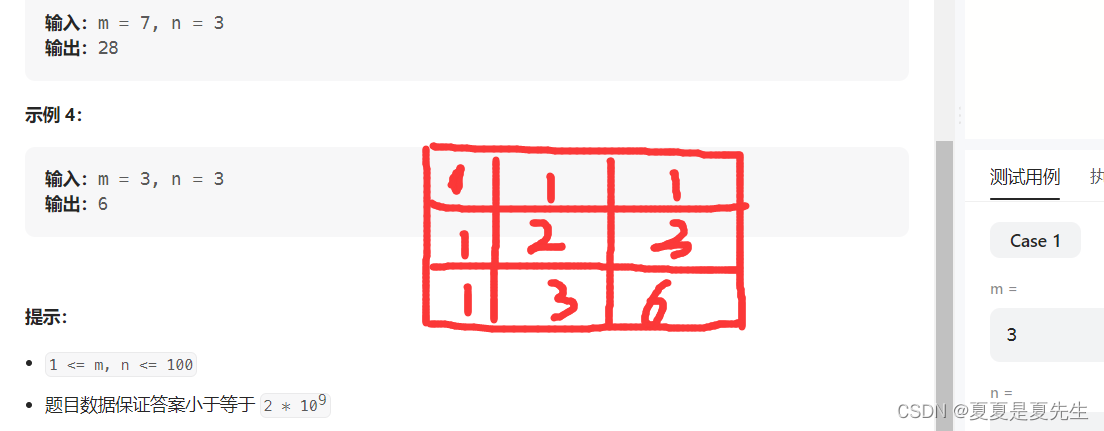
如示例4可知，因为每次只能向左或向下走，所以dp数组中的第0行和第0列都只有一种路径可走。对于其他位置，每个位置的不同路径等于相邻的左边位置的路径数加上相邻的上边位置的路径数。即存在递推关系：

dp[i][j] = dp[i-1][j] + dp[i][j-1]  其中i>=1 && j >=1

确定遍历顺序
遍历顺序，从左到右顺序遍历即可

3 代码实现

public int uniquePaths(int m, int n) {
        //确定dp数组 dp[i]表示走到第i个位置有多少种不同路径
        int[][] dp = new int[m][n];

        //初始化dp
        //因为只能向右或向下走，所以第0行的所以位置只有一种的路径，因此将dp的第一行初始化为1
        for (int i = 0;i<n;i++){
            dp[0][i] = 1;
        }
        //同理，第0列也只有一种路径可走 因此将第0列初始话为1
        for (int j=0;j<m;j++){
            dp[j][0] = 1;
        }

        //递推公式 dp[i][j] = dp[i-1][j] + dp[i][j-1]  其中i>=1 && j >=1
        //遍历顺序 从左到右顺序遍历即可
        for (int i=1;i<m;i++){
            for (int j=1;j<n;j++){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }