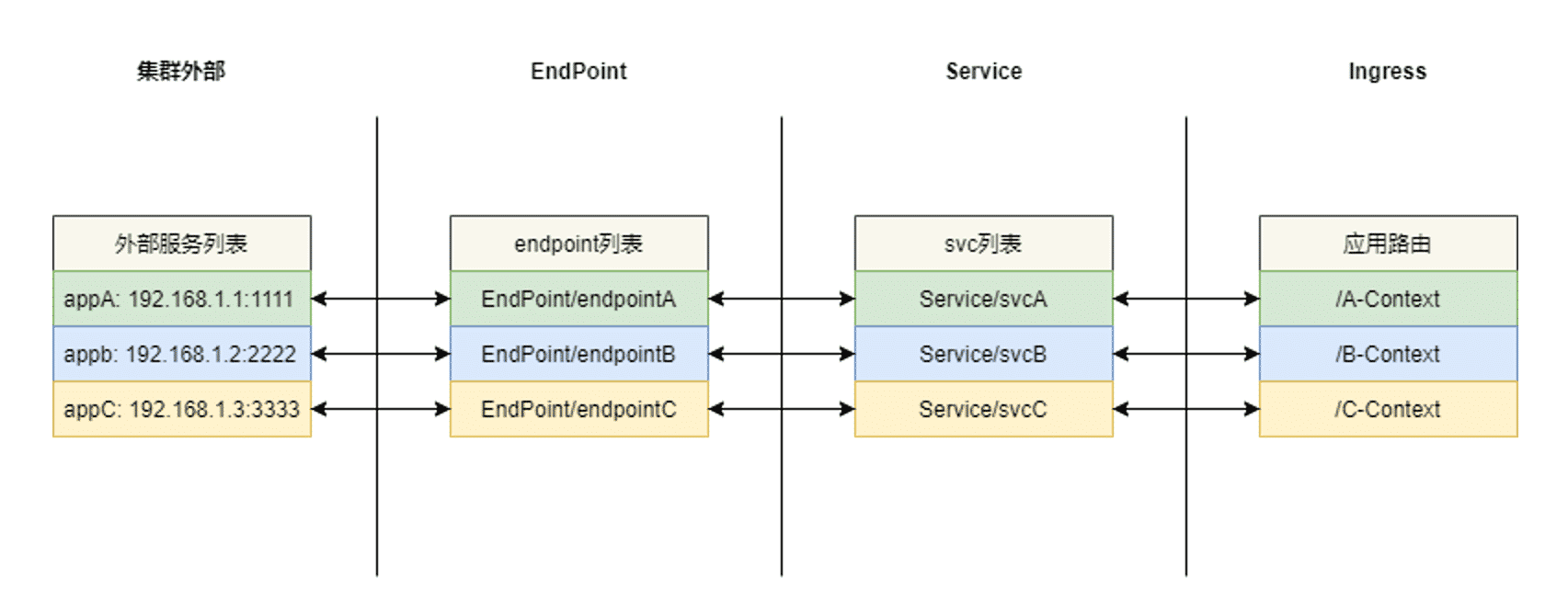
当然了昨天晚上写了求两源点之间最少权值和,就不得不再写一下另外两个求最小生成树的算法分别是克鲁斯卡尔和普利姆了,话不多说直接进入主题
目录
并查集:
克鲁斯卡尔算法(与并查集结合起来):
普利姆算法:
并查集:
为啥先说并查集,因为对我们下面看克鲁斯卡尔有用,先引入并查集的例子进行初步讲解
首先什么是并查集:其实通俗来讲就是将一系列有特定关系的事务给他总合起来
举一个简单例子Eg:比如a跟b有关系,b是a的父亲,然后a和c是兄妹关系,那么b也就是c的父亲
所以就是按图表示为
第一种:a->b,a-c(平级)=>c->b
第二种:a->b,b->c=>a->b->c
第三种:a->b->e,c->e=>(a,c,b)->e
这就是大体理解一下,为了做到上面的效果我们需要两个数组来存储,第一个用来存储每一个节点的祖先分别是什么,第二个用来存储当前节点的祖先下面有几个子节点
先看初始化:
void Init(int n)
{
for(int i=1; i<=n; i++)
{
arr[i]=i; //arr是当前节点的祖先节点,所以刚开始每个人的祖先节点都是自己本身
rank[i]=1; //当前下面的子节点只有本身节点所以就为1
}
}然后就是寻找祖先节点:
int find(int x)
{
if(x==arr[x]) //如果是当前节点的祖先就是自己那就直接返回
{
return x;
}
else
{
return arr[x]=find(arr[x]); //如果是其他节点,就继续去寻找其他节点直到找到最终的祖先节点
}
}然后将节点进行结合:
void unite(int x,int y)
{
x=find(x); //首先找两个节点的祖先节点
y=find(y);
if(x==y) //如果祖先是同一个节点那就不需要结合
{
return;
}
if(rank[x]<rank[y]) //不一样看当前的级别,谁的级别高谁就是他们两个的总结点
{
arr[x]=y;
}
else
{
arr[y]=x;
if(rank[x]==rank[y])
{
rank[y]++; //如果相同级别看你当前是将谁赋予了祖先节点,如果是x为祖先节点,则y++,反之亦然
}
}
}
克鲁斯卡尔算法(与并查集结合起来):
众所周知啊克鲁斯卡尔(Kruskal)算法就是用边权值进行寻找最小生成树,先将边的最小值进行一个排序然后从最小值开始寻找生成一颗完整的树
但是存在一个问题就是说什么情况下可以称作为一颗完整的树呢?
答案很简单我们用并查集来解决找祖先的问题。
所以我们先将整个已知条件进行按权值排序,这里用啥都行,希尔,快排,归并,冒泡都可以
我用的冒泡(简单一点):
void sort(int m)
{
Node N;
for(int i=1; i<=m; i++)
{
for(int j=i; j<=m; j++)
{
if(a[i].e>a[j].e)
{
N=a[i];
a[i]=a[j];
a[j]=N;
}
}
}
}然后就是实现克鲁斯卡尔算法了:
int kruskal(int n,int m)
{
int result=0,n_edge=0,f1,f2,j=1;
for(int i=1; i<=m; i++)
{
f1=find(arr[a[i].edga_first]); //先找两人的共同祖先
f2=find(arr[a[i].edga_second]);
if(f1!=f2) //一样的话就不用算了
{
unite(f1,f2); //不一样直接合并因为我们已经按最小权值进行了排序
result+=a[i].e; //将当前的总权值进行跟新
n_edge++; //表明当前的树有几个节点
}
if(n_edge==n-1) //如果节点数已经够了总结点就可以退出了
{
return result;
}
}
return -1; //如果无法生成最小数就返回-1
}看看整体实现
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define max 200005
typedef struct graph //定义一个结构体保存边边权三个值
{
int edga_first,edga_second;
int e;
} Node;
int arr[max],rank[max]; //arr为祖先节点的定义,rank为当前祖先节点的子节点数
Node a[max];
void sort(int m)
{
Node N;
for(int i=1; i<=m; i++)
{
for(int j=i; j<=m; j++)
{
if(a[i].e>a[j].e)
{
N=a[i];
a[i]=a[j];
a[j]=N;
}
}
}
}
void Init(int n)
{
for(int i=1; i<=n; i++)
{
arr[i]=i;
rank[i]=1;
}
}
int find(int x)
{
if(x==arr[x])
{
return x;
}
else
{
return arr[x]=find(arr[x]);
}
}
void unite(int x,int y)
{
x=find(x);
y=find(y);
if(x==y)
{
return;
}
if(rank[x]<rank[y])
{
arr[x]=y;
}
else
{
arr[y]=x;
if(rank[x]==rank[y])
{
rank[y]++;
}
}
}
int kruskal(int n,int m)
{
int result=0,n_edge=0,f1,f2,j=1;
for(int i=1; i<=m; i++)
{
f1=find(arr[a[i].edga_first]);
f2=find(arr[a[i].edga_second]);
if(f1!=f2)
{
unite(f1,f2);
result+=a[i].e;
n_edge++;
}
if(n_edge==n-1)
{
return result;
}
}
return -1;
}
int main()
{
int n,m,p,q,ans;
printf("请输入当前的节点总数和已知条件数:\n");
scanf("%d%d",&n,&m);
Init(n);
printf("分别按照边1,边2,权值的方式进行输入,总共输入%d条:\n",m);
for(int i=1; i<=m; i++)
{
scanf("%d%d%d",&a[i].edga_first,&a[i].edga_second,&a[i].e);
}
sort(m);
p=kruskal(n,m);
if(p==-1)
{
printf("无法生成最小生成树\n");
}else{
printf("最小生成树的总权值为:%d\n",p);
}
return 0;
}
/*
测试样例
6 10
1 3 4
1 2 3
1 6 1
6 2 5
6 5 3
2 3 2
2 4 4
5 4 7
4 3 6
5 2 5
*/给一个样例图:
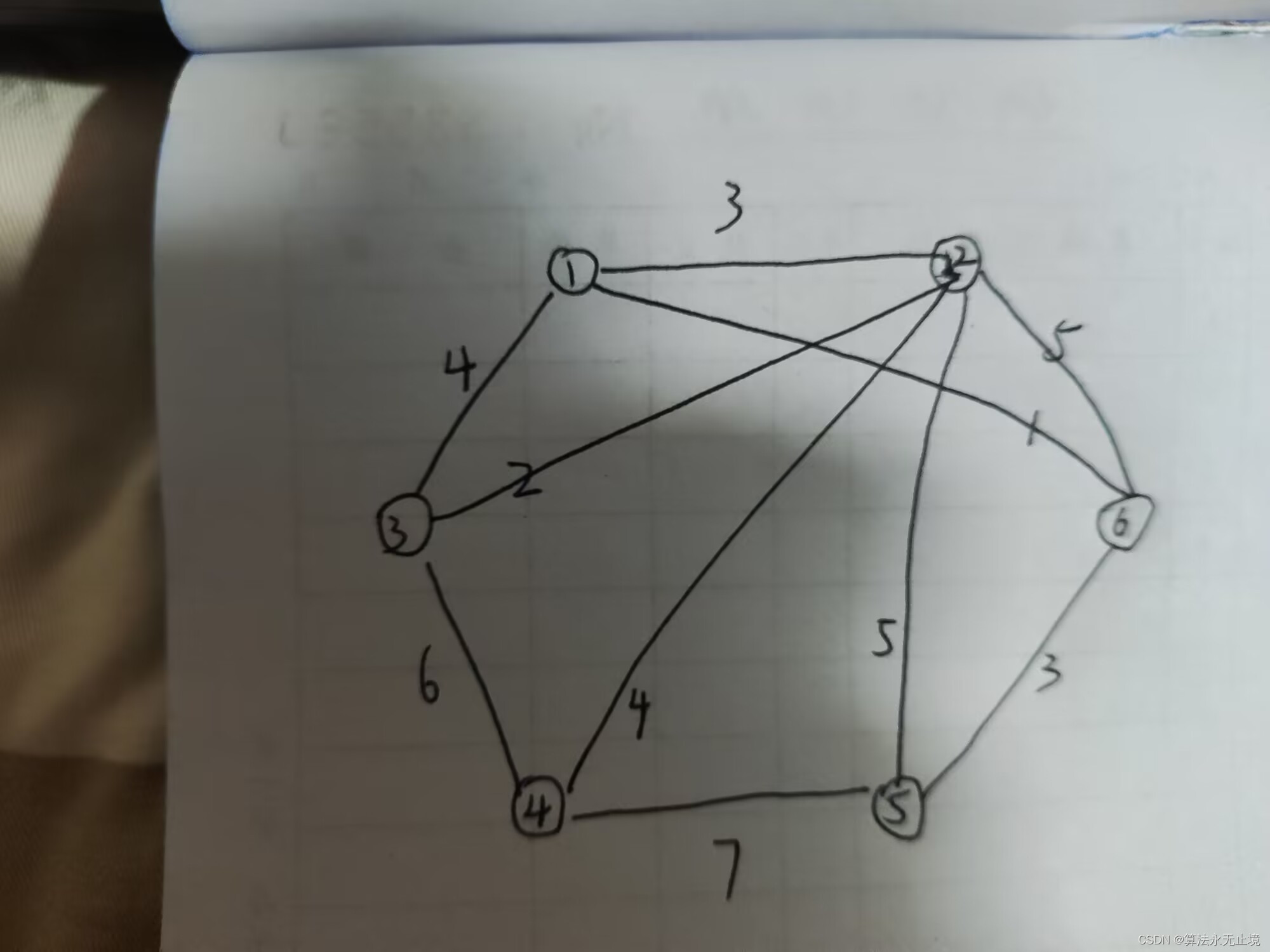
最小生成树如下:
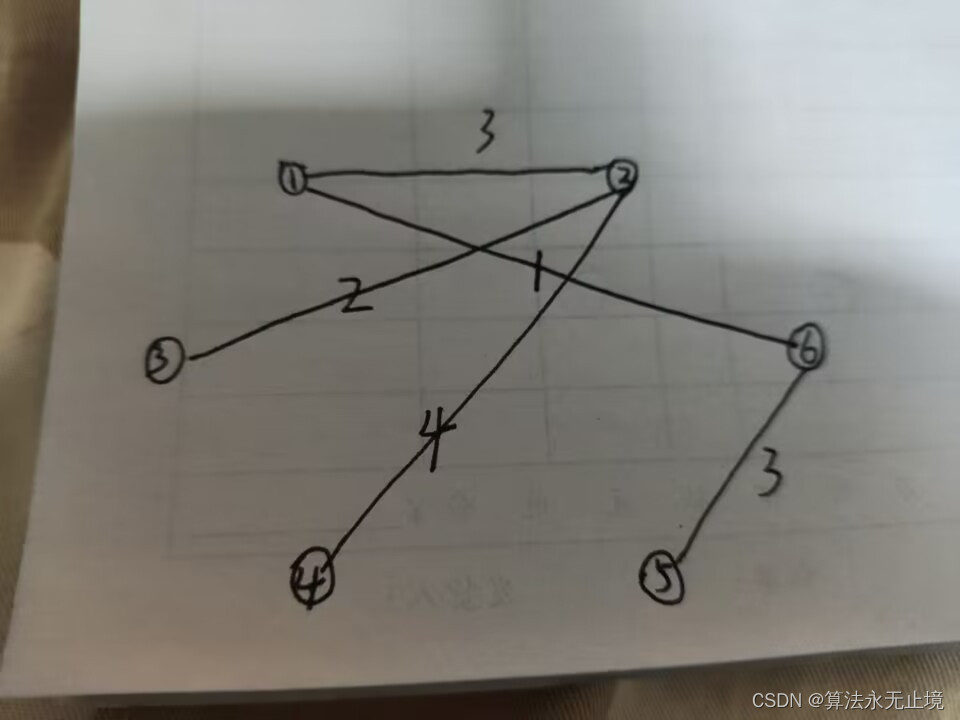
代码实测运行图:
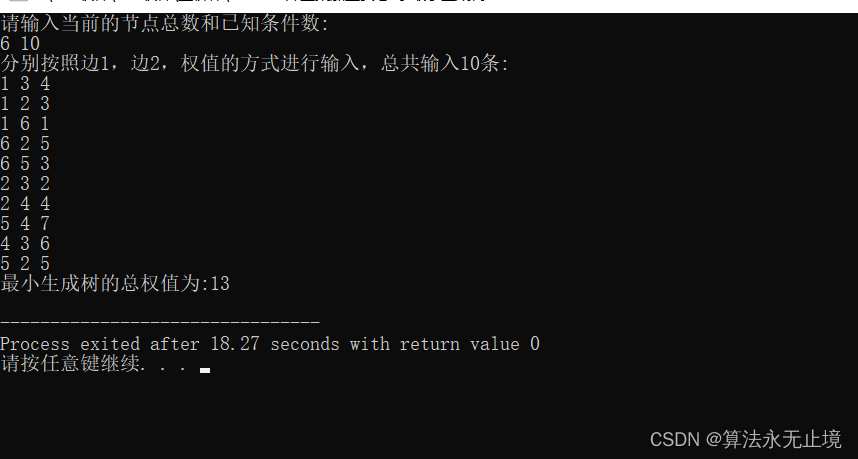
普利姆算法:
![[附源码]Python计算机毕业设计高校教学过程管理系统Django(程序+LW)](https://img-blog.csdnimg.cn/ae62f73dfc05487987426bdeceae49b7.png)