文章目录

1.二叉树的概念

1.1概念

1.2存储方式

1.3特殊的二叉树

1.4规律

2.二叉树的实现

2.1表现方式

2.2遍历

2.2.1前序遍历

思想

代码

详细分析

2.2.2中序遍历

2.2.3后序遍历

2.2.4层序遍历

思想

代码

详细过程

1.二叉树的概念

1.1概念

一棵二叉树是结点的一个有限集合，该集合为空，或者是由一个根节点加上两棵称为左子树和右子树的二叉树组成。

二叉树的特点：

（1）每个结点最多有两棵子树，即二叉树不存在度大于2的结点。
（2）二叉树的子树有左右之分，其子树的次序不能颠倒。

1.2存储方式

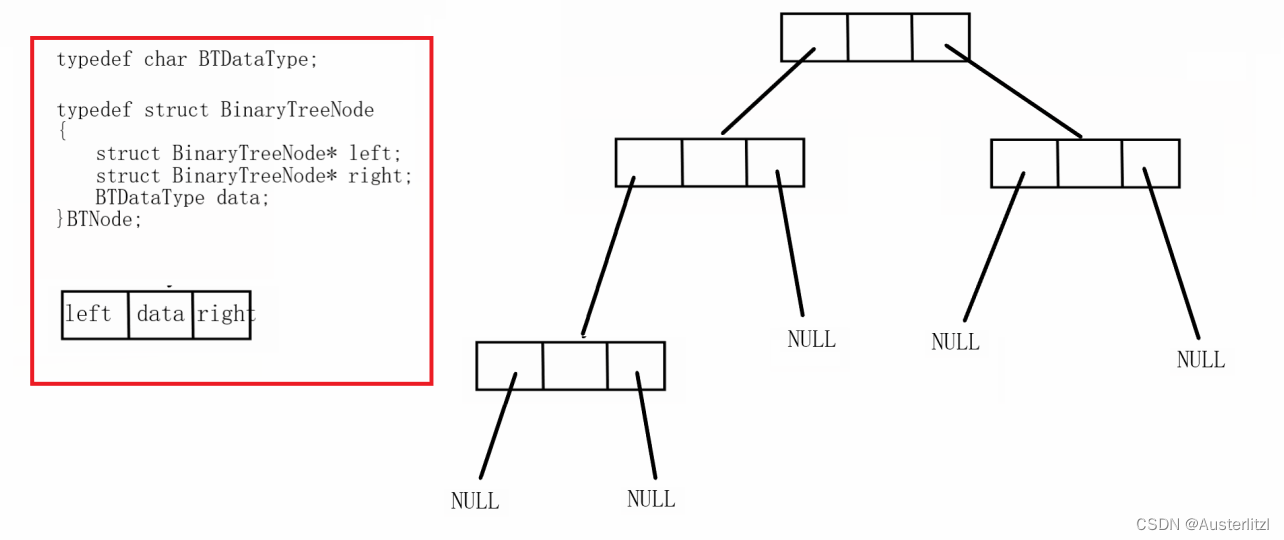
二叉树可以采用线性结构或者非线性结构实现。线性结构有比如堆，本文使用非线性结构实现。既然非线性，那就肯定要使用类似链表的结构。在这里，由于二叉树每个节点都有最多两个孩子，我们使用有 一个数据域 和两个指针域 的结构来表示。

如下图，左边红色框内分别表示二叉树的定义，以及每一个节点的结构。右边表示二叉树的逻辑结构。

1.3特殊的二叉树

（1）满二叉树

每一层的结点数都达到最大值，则这个二叉树就是满二叉树。
也就是说，如果一个二叉树的层数为h（根节点是第1层），且结点总数是(2^h) -1 ，则它就是满二叉树。比如下图：

（2）完全二叉树

完全二叉树的叶子结点只能出现在最下层和次下层，且最下层的叶子结点从左到右连续；前K-1层是满的二叉树。

如下四种，都是完全二叉树。值得注意的是，满二叉树也是完全二叉树，其倒数第二层是满的，最后一层叶子节点从左到右连续，满足。

（3）非完全二叉树

非完全二叉树也很好理解，不满足完全二叉树的条件。比如下面两种，左边是最后一层叶子节点从左到右不连续，右边是倒数第二层没有满。

1.4规律

1.有h层（根节点算第一层）的满二叉树，最后一层的节点个数为 2^(h-1) 。

这并不难理解，由于每一个节点都有两个孩子节点，相当于每一层的节点个数都是上一层的两倍。第一层是1个，第二层2个……第h层是2^(h-1) 个。观察下图结构可以验证。

2.有h层（根节点为第一层）的满二叉树总结点个数为 2^h -1 。

这并不难理解。2^h -1 可以看作 2^(h-1) + 2^(h-1) -1 。2^(h-1) 就是满二叉树最后一层的节点个数，所以 2^(h-1) -1 可以看作，前 h-1 层的节点个数，事实上也是这样，对照上面的满二叉树或者任一满二叉树都可以得到这样的结论。

3.二叉树总节点个数=总度数+1。

如下，把除了根节点之外，所有节点都和链接它的那根线相连，当作一个小整体。有多少个小整体，就有多少个节点（不包括根节点）。由于每一个小整体里面有一根线和一个节点，这条线可以看作度，所以有多少个节点就有多少个度（除去根节点）。所以，总节点个数=度数+1。相当于其他所有节点个数+1。

2.二叉树的实现

2.1表现方式

上文已有说明，用结构体，里面包含一个数据域和两个指针域，指针域分别指向左右孩子节点。


typedef char BTDataType;

typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

2.2遍历

本文讲述的是递归实现遍历，所以要关注递归的几个注意点：

递归的两个基本要素：
1、递归关系式：确定关系式，即原问题是如何分解为子问题的
2、递归出口：确定递归到什么时候终止。

同时、一个递归函数我们是默认它能够完成所需功能的。

2.2.1前序遍历

思想

前序遍历顺序：根、左子树、右子树。

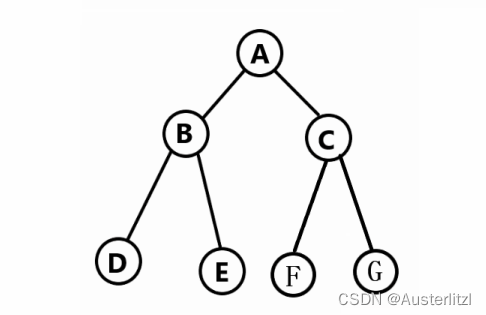
上述二叉树，前序遍历顺序是：A -> B -> D -> E -> C。从递归两个基本要素来看，递归关系式就是：先打印根节点数据，然后前序遍历根节点的左子树，遍历完之后，再前序遍历根节点的右子树。递归出口：当遍历到的节点为空，那么就return。

如下代码，为什么前序遍历左右子树可以直接 PrevOrder(root->left) ; 和 PrevOrder(root->right)；因为，我们默认这个递归函数是可以实现其功能的，现在暂时不要进行更深层次的思考。

代码

//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)           //终止条件
	{
		printf("NULL ");
		return;
	}
	printf("%c ", root->data);  // 先打印当前节点
	PrevOrder(root->left);      // 前序遍历左子树
	PrevOrder(root->right);     // 前序遍历右子树
}

详细分析

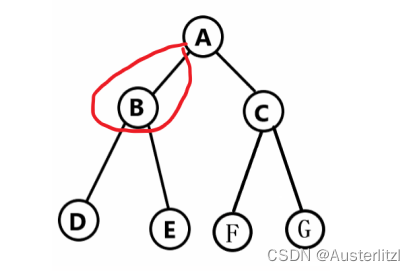
看到代码，先不要疑惑，一步一步走，最开始一定是要生成一个对应的二叉树，然后才可以前序遍历，如下：

一开始传入的 a 节点，就是根节点为PrevOrder() 的root参数，进入该函数之后，会判断其是否为空？不为空，那么打印该节点的数据，即"A"，然后PrevOrder(root->left); 注意，现在的 root 是 a，那么 a 节点的左孩子是 b 节点，相当于以 b 节点为 root 参数，又进入了 PrevOrder() 函数，并进行和之前类似的操作。

但是，这里要注意，进入PrevOrder(root->left); 之后，以 a 节点为函数的 root 参数那块并没有结束，因为在那块函数里进入了以 b 节点为 root 的函数，如下过程。一直到进入 d 节点的左孩子，d 节点的左孩子为NULL，那么NULL为参数 root ，进入 PrevOrder() 函数，毫无疑问根据 if 语句会打印NULL并return。

这里又来问题了，上图的 return 是 return 到哪里呢？是直接return 到以根节点为 root 参数那里吗？显然不是，实际上是返回"上一级"，如下图，通过步骤4（黑色数字标记），返回到 d 节点为root参数的那里，那么返回之后执行什么呢？根据前序遍历函数的代码，还要PrevOrder(root->right); 由于 root 是 d 节点，其右孩子也是NULL，所以也直接返回，即步骤5、6。

到这里，以 d 节点为参数 root 的过程算是执行完毕，但是，该过程也是以 b 节点为 root参数的中间过程，所以该过程结束后，也要返回以 b节点为 root 参数的进程当中。如步骤7。

把上图的最后一步，当作第一步来看，继续分析接下来的过程。如下图：

既然以 b 节点为 root 参数的这个过程，其 PrevOrder(root->left); 过程已经完成，接下来就是执行 PrevOrder(root->right); 这里 b 节点的右孩子是 e 节点，如下，过程和上面比较相似，也就不详细说明，步骤按顺序来即可。

在以 b 节点为 root 参数的过程中，PrevOrder(root->right); 也结束之后，该过程就结束了，返回“上一级”，其上一级是以根节点为root 参数。那么返回到哪里呢？

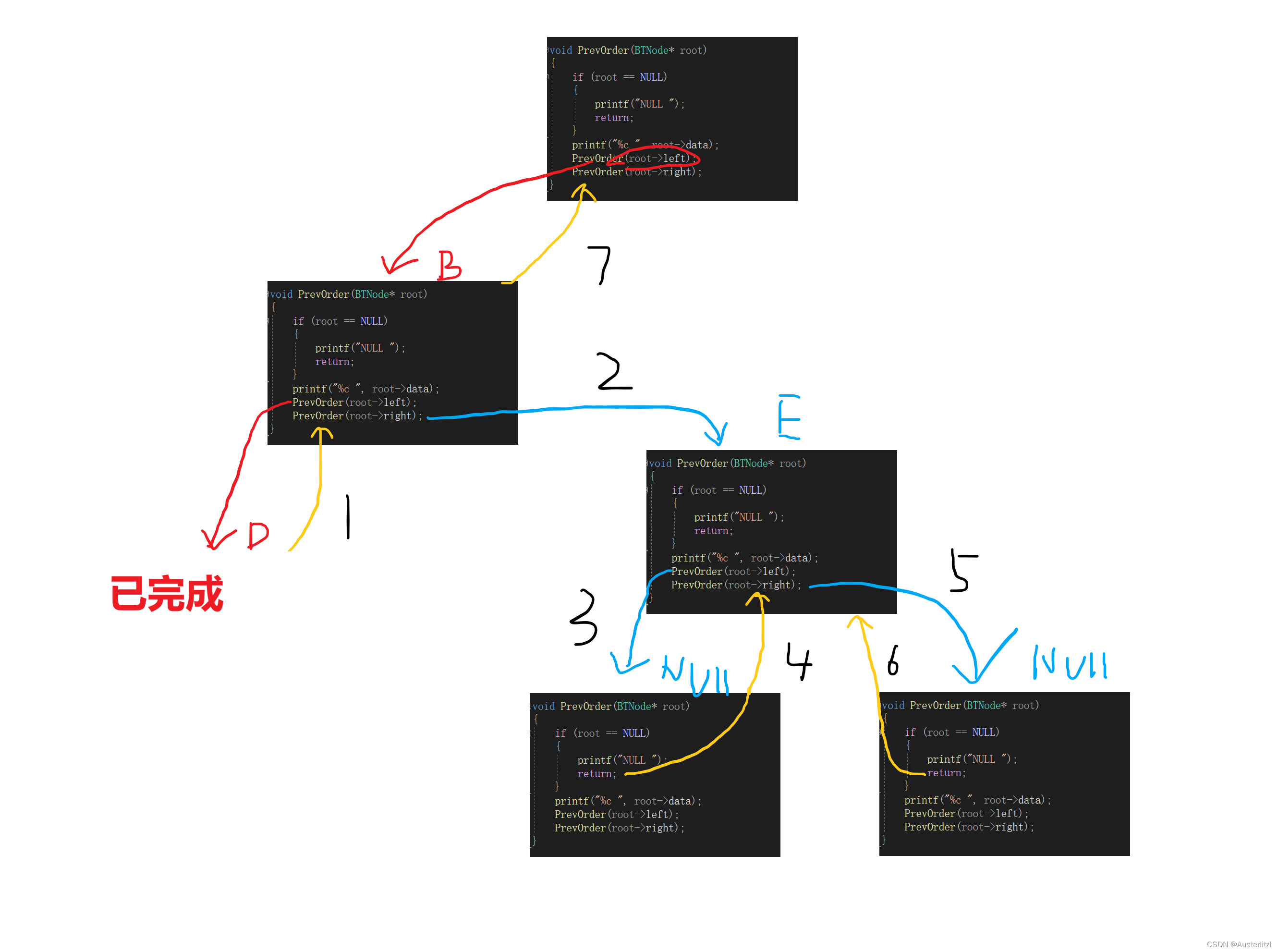
如下图，由于以b节点为root 参数的过程，实际上也是以根节点为root 参数的过程里面的一部分，所以该过程结束之后，自然是执行下面的代码。执行 PrevOrder(root->right); 在该过程里面，root是根节点，所以其右孩子是c 节点。

以 c 节点为root 参数的过程也不详细展开，都大体差不多，按照下面标记的顺序来看即可。最后，执行完该过程，那么以根节点为root 参数的过程才算是执行完毕，整个函数也就执行完，前序遍历结束。

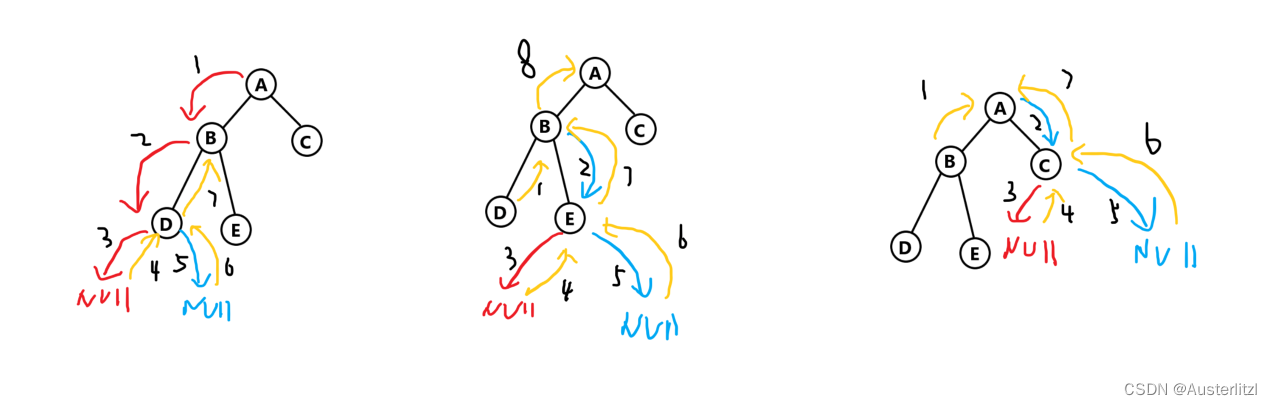
其整个过程大致如下所示，可以看到是一层一层下去，然后返回来。

当然，也可以如下一样理解，顺序按照标记的顺序来即可：

2.2.2中序遍历

中序遍历顺序：左子树、根，右子树。

中序遍历实际上和前序遍历差不多，也就是打印数据的顺序有所区别，代码如下。可以看出，和前序遍历的区别仅仅在于：先遍历左子树，还是先打印当前节点的值。

其根据递归的思想来看也是。递归终止条件自然一样。那么递归关系式：先中序遍历左子树，遍历完之后，打印根节点，然后中序遍历右子树，整个中序遍历结束。就是如此简单，从代码上来看也是，默认其能实现递归过程，直接这样写。

其详细分析过程和前序遍历差不多，可以自己尝试画一画，对理解递归遍历二叉树很有帮助！！！

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

2.2.3后序遍历

后序遍历顺序：左子树、右子树，根。

后序遍历和中序遍历同理。其递归关系式：先遍历左子树，遍历结束之后，再遍历右子树，最后打印根节点。

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

2.2.4层序遍历

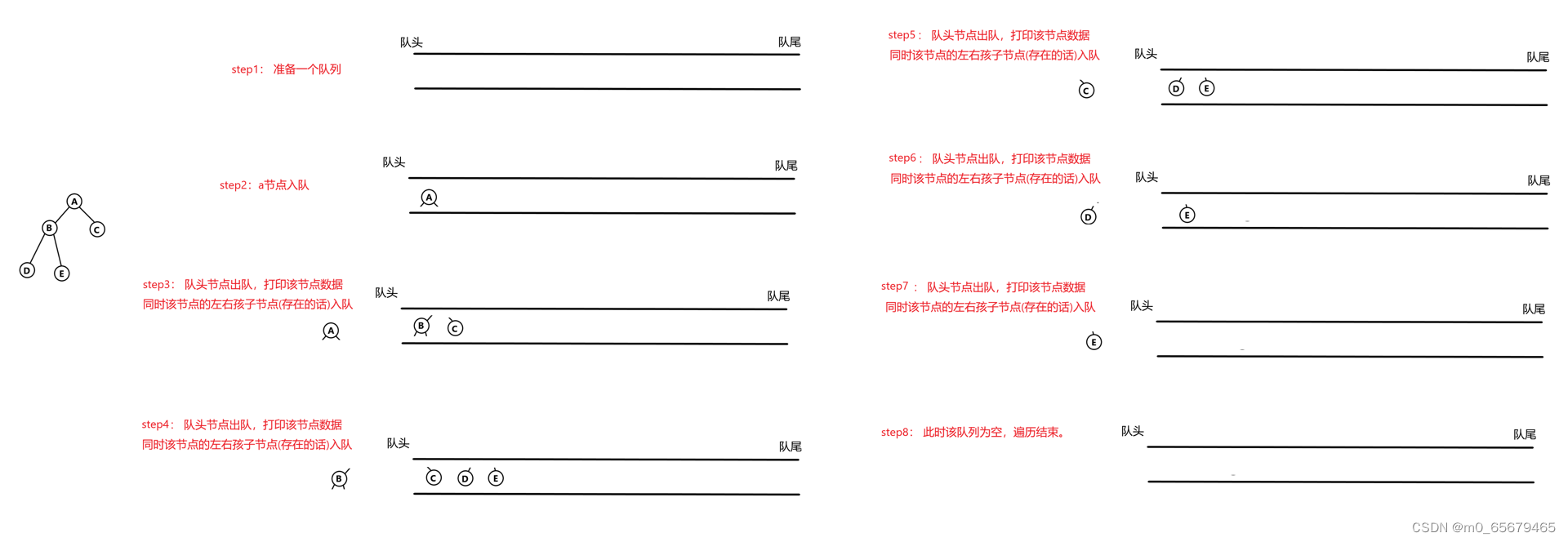
思想

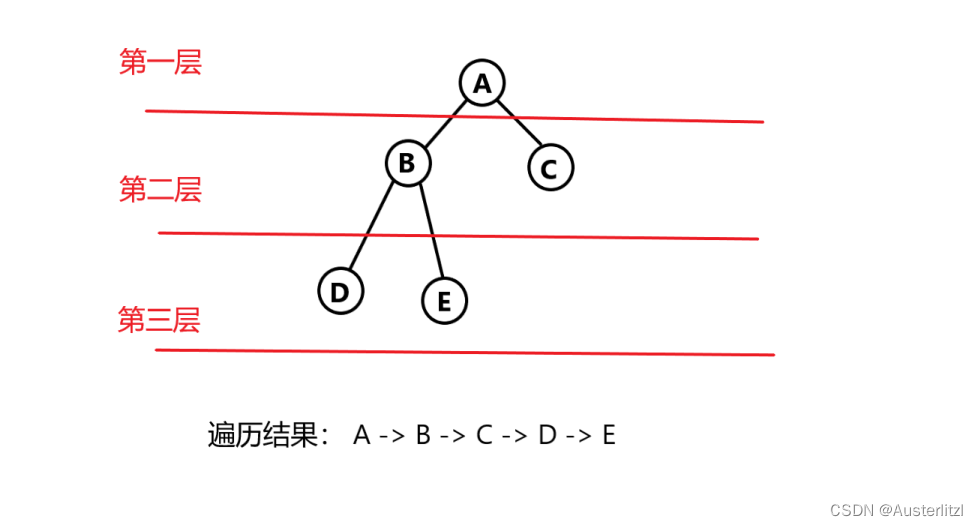
层序遍历：按照层数从上到下，每一层从左到右来遍历。

层序遍历，又被称作广度优先遍历。遍历结果如下图，这样子的遍历方式，当然不是直接递归就可以实现的，而是要根据队列 “先入先出” 的特点，借助队列来完成。

其主要完成的方法就是：先把节点 a 入队，然后取到该节点，并出队，打印该节点的值（"A"），并且将节点 a 的左孩子入队，右孩子入队。接下来就是重复类似的过程：取队头节点，然后出队，打印取出的节点数据，将取出节点的左右孩子分别入队。一直到队列为空。

代码

如下，由于while 循环结束条件是队列为空，所以一开始要先入队一个数据。

循环过程，每次都把队头数据取出来，用temp 指针指向该数据，然后出队，打印temp 指向的节点的数据。然后把temp 左右孩子节点入队。

注意，这里入队顺序不能变，必须是先入左孩子，再入右孩子。因为每个节点最多只有两个孩子节点，每次按顺序先入左孩子，队列里每个节点的左孩子就先出，这才符合层序遍历的要求。


//层序遍历   广度优先遍历
void LeafSort(BTNode* root)
{
	assert(root);
	//创建一个队列
	Queue p;
	QueueInit(&p);
	if (root)
		QueuePush(&p, root);
	while (!QueueEmpty(&p))
	{
		BTNode* temp = QueueFront(&p);//先把第一个取出来
		QueuePop(&p);
		printf("%c ", temp->data);
		if (temp->left)
		{
			QueuePush(&p, temp->left);
		}
		if (temp->right)
		{
			QueuePush(&p, temp->right);
		}
	}
	return;
}