博弈论是二人或多人在平等的对局中各自利用对方的策略变换自己的对抗策略,达到取胜目标的理论。博弈论是研究互动决策的理论。博弈可以分析自己与对手的利弊关系,从而确立自己在博弈中的优势,因此有不少博弈理论,可以帮助对弈者分析局势,从而采取相应策略,最终达到取胜的目的。
01、最小最大问题
最小最大问题( minimax ):用于确定计算机玩家在诸如井字游戏、跳棋、奥赛罗和国际象棋中的哪一步。这类游戏被称为完美信息游戏,因为它可以看到所有可能的动作。拼字游戏并不是一个完美信息的游戏,因为你看不到对手的手,所以无法预测对手的动作。
可以把这个算法想象成人类的思维过程:如果我做这个动作,那么我的对手只能做两个动作,每个动作都会让我赢。所以这是正确的选择。
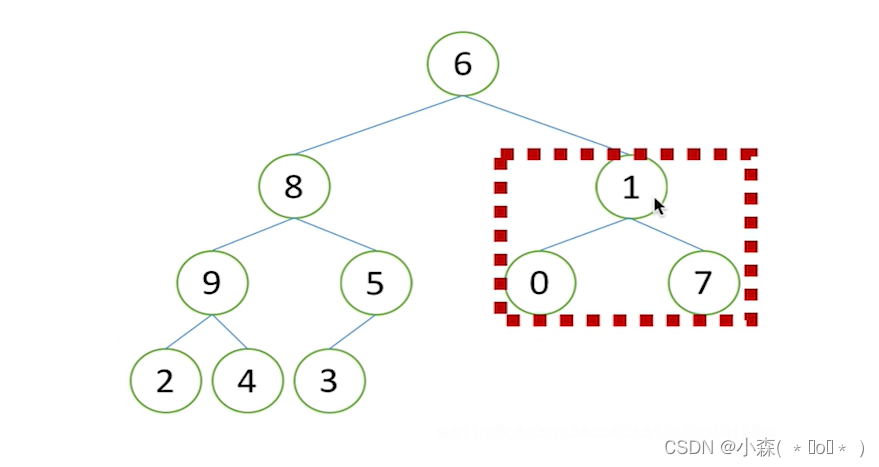
用博弈树数据结构表示井字游戏如图 1 所示。
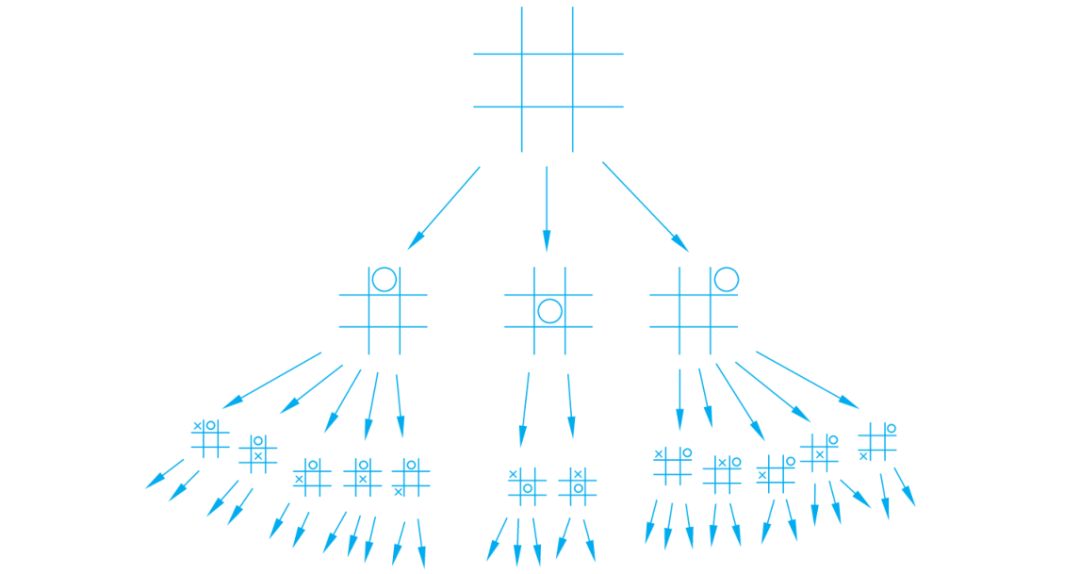
■ 图1 用博弈树数据结构表示井字游戏
如果你认为所谓最小最大就是穷举过程中找到的最差走法和最佳走法那就错了,既然是对立的概念,当然是两个对象,这里的最小最大是当前轮到 AI 走了, AI 进行穷举并选择一条对于 AI 来说最佳而对于人来说最差的走法,但是再考虑一下,机器也是有限的,对于象棋这样棋盘较大的游戏,穷举完博弈树在当前科技下不可能,因此我们的最小最大算法需要一个深度,即向前走几步,计算机就能在这个指定的比较小的整数下完成对博弈树的穷举。
当遍历若干树枝后不可能就结束了,如果在游戏没有结束的情况下我们还需要一个评价启发函数,这个函数用于判断当前策略的价值,如果使用某走法能赢,就返回一个大的正数;如果这种走法会输,就返回一个大的负值;如果走法会产生和局,就返回一个 0 左右的数;如果由于当前博弈树深度没办法判断局面,那么评价函数就会返回一个启发值。
参考程序:
#include<cstdio>
int MaxMin(int depth,int player mode)
{
int best = INFINITY(player mode);
//player mode 是参照物,如果当前落子是人,则返回一个很小的值,反之返回一个很大的值
if (depth <= 0) //当前以局面为博弈树的根
return Evaluate() ; //估值函数
}
GenerateLegalMoves () ;//生成当前所有走法
while (MovesLeft () ) //遍历每一个走法
{
MakeNextMove () ;//实施走法
val = -MaxMin(depth - 1);//换位思考
UnmakeMove() ;//撤销走法
if (val > best)
best = val;
return best;
} 02、巴什博弈
A和B一块报数,每人每次最少报1个,最多报4个,看谁先报到30。这应该是最古老的关于巴什博弈(Bash game)的游戏了。
其实如果知道原理,这个游戏一点运气成分都没有,只和先手、后手有关,比如第一次报数,A报k个数,那么B报5-k个数,那么B报数之后问题就变为,A和B一起报数,看谁先报到25了,进而变为20,15,10,5,当到5的时候,不管A怎么报数,最后一个数肯定是B报的,可以看出,作为后手的B在个游戏中是不会输的。
那么如果要报n个数,每次最少报1个,最多报m个,我们可以找到这么一个整数k和r,使n=k*(m+1)+r,代入上面的例子可以知道,如果r=0,那么先手必败;否则先手必胜。
巴什博弈: 有n个物品,两个人轮流从中取物,规定每次最少取1个,最多取m个,最后取光者为胜。
参考程序:
#include <iostream>
using namespace std;
int main()
int n,m;
while(cin>>n>>m)
cout<<"后手必胜“< <endl;if(n%(m+1)==0)else cout<<"先手必胜"< <endl;
return 0;例题如下。
题目大意: 小唐和小红轮流写数字,小唐先写,每次写的数x满足1≤x≤k,小红每次写的数y满足1≤y-x≤k,谁先写到不小于n的数算输。
结论: r=(n-1)%(k+1),r=0时小红胜,否则小唐胜。
详解:
巴什博弈: 同余理论。
从n个物品中两人轮流取,每次取1~m个,最后取完者为胜。
比如10个物品,每次只能取1~5个,则先手方必赢。
(1) 面对[1…m]个局面,必胜。
(2) 面对m+1个局面,必输。
(3) 如果可以使对手面临必输局面,那么是必赢局面。
(4) 如果不能使对手面临必输局面,那么是必输局面。
基础: 1, 2,…, m是必赢局面,m+1是必输局面。
递推: m+2,m+3,…,2m+1是必赢局面,2m+2是必输局面。
k(m+1)是必输局面,应该允许k=0,因为0显然也是必输局面。
在必输局和必赢局中,赢的一方的策略是: 拿掉部分物品,使对方面临k(m+1)的局面。
例如,上例中10个物品,只能拿1~5个,先手方拿4个即可,对手无论拿多少个,你下次总能拿完。
从另一个角度思考这个问题,如果物品数量随机,那么先手方胜利的概率是m/(m+1),后手方胜利的概率是1/(m+1)。
03、斐波那契博弈
两人轮流从一堆物品中取物品,先手最少取一个,至多无上限,但不能把物品取完,之后每次取的物品数不能超过上次取的物品数的二倍且至少为一件,取走最后一件物品的人获胜。
结论:先手胜当且仅当 n 不是斐波那契数(n 为物品总数)。
# include <iostream>
# include <string.h>
# include <stdio.h>
using namespace std;
const int N = 55;
int f[N];
void Init()
{
f[O] = f[1] = 1;
for(int i=2;i<N;i++)
f[i] = f[i-1] + f[i-2];
}
int main()
{
Init();
int n;
while(cin>>n)
if(n == 0) break;
bool flag = 0;
for(int i=0;i<N;i++)
{
if(f[i] == n)
{
flag = 1;
break;
}
if(flag) puts("Second win") ;
else
puts("First win");
R
}
return 0;
}