1. 归并排序原理
归并排序(MERARE-SORT)简单来说就是将大的序列先视为若干个比较小的数组,分成比较小的结构,然后是利用归并的思想实现的排序方法,该算法采用经典的分治策略(分就是将问题分成一些小的问题分别求解,而治则将分的阶段得到的各答案“合”在一起)。
归并排序算法就是应用归并思想的一个典型例子。在归并排序中,我们首先将未排序的数组不断地划分成两个子数组,直到子数组的长度为1。然后,我们合并子数组,使得子数组按照排序规则排列,最后得到排序完成的数组。
分治法可以看作是"分而治之"的意思,也就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,从而使得原问题的解即子问题的解的合并。
都需要递归地解决子问题,并在最后合并子问题的解。

- 上图就是将 一个大的数组二分成一个个小的数组,知道最后每个划分的数组只有一个元素的时候,开始进行合并,这种操作就是分阶段,可以理解为递归拆分子序列的过程,递归的深度为logn。
- 治阶段,将两个已经有序的子序列合并成一个有序序列。
遍历时处理元素的过程:
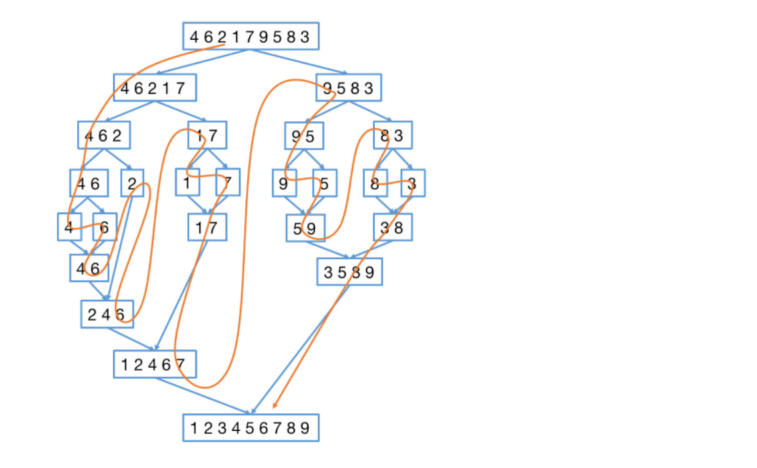
总结归并排序的思路:
- 首先将原数组二分的拆分,直到最后问题变成最小的时候,也就是每个子数组只有一个元素,开始进行第二步。
- 将两个子数组合并,按照合并两个有序数组的方式进行,按照图中每个左右子树从下往上,然后再将左右子树合并,每个子树最后都是一个有序数组。
public static void mergeSort(int[] array, int start, int end, int temp[]){
if (start >= end){
return;
}
mergeSort(array, start, (start + end) / 2,temp);
mergeSort(array, (start + end) / 2 + 1, end,temp);
merge(array, start, end, temp);
}
public static void merge(int[] array, int start, int end, int[] temp){
int middle = (start + end) /2;
int left = start;
int right = middle + 1;
int index = left;
//将两边的最小元素移到左边
while (left <= middle && right <= end){
if (array[left] < array[right]){
temp[index++] = array[left++];
}else {
temp[index++] = array[right++];
}
}
//左端元素遍历完,依次把右端元素转移过来
while (left <= middle){
temp[index++] = array[left++];
}
//左端元素遍历完,依次把右端元素转移过来
while (right <= end){
temp[index++] = array[right++];
}
//将temp中的元素依次转到array中,
for (int i = start; i <= end; i++){
array[i] = temp[i];
}
}